Признак параллелограмма по противоположным сторонам. Параллелограмм. Закрепление изученного материала

22.10.2014 Классная работа . Тема урока « », п. 43 . I. «Рабочая тетрадь»
11.

II . Атанасян , № 376 (б, д), 372 (а, б), 371 (б)

ПРИЗНАК ПАРАЛЛЕЛОГРАММА.

III . ПРИЗНАКИ ПАРАЛЛЕЛОГРАММА

1 0 . Если в четырехугольнике ,

то этот четырехугольник – параллелограмм .

2 0 . Если в четырехугольнике противоположные стороны попарно равны , то этот четырехугольник – параллелограмм.

3 0 . Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам , то этот четырехугольник – параллелограмм .

Домашнее задание для педагога 2016

Выучить теорию: п. 42, 43

Задачи: Базовый уровень: № 371 (а), 372 (в), 376 (в, г)

Повышенный уровень:

1 0 . Если в четырехугольнике две стороны равны и параллельны , то этот четырехугольник – параллелограмм . Дано: 1) ABCD -четырехугольник 2) АВ|| CD , AB = CD . Доказать, что ABCD – параллелограмм Доказательство:

1) Дополнительное построение: диагональ АС. 2) Рассмотрим АВС и СDА АС – общая сторона АВ=СD, по условию (накрест лежащие углы при прямых АВ|| CD и секущей АС ) Значит, АВС = СDА ( ) Но - накрест лежащие углы при прямых ВС и AD и секущей АС , значит ВС || AD 4)В четырехугольнике ABCD противолежащие стороны АВ|| CD , ВС || AD , значит, ABCD – параллелограмм (по определению )

Для педагога 2016

3 0 . Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм .

Дано: 1) ABCD -четырехугольник

2) АВ|| CD , AB = CD .

Доказать, что ABCD – параллелограмм

Доказательство:

1) Рассмотрим AOB и COD

АО=ОС, по условию

ВО=ОD, по условию

как вертикальные углы

Значит, AOB =COD (по двум сторонам и углу между ними )

3) Соответствующие элементы треугольников равны, тогда AB = CD , , но AB и CD и секущей AC , значит AB || CD (по признаку параллельных прямых)

4)В четырехугольнике ABCD противолежащие стороны AB || CD , AB = CD , значит, ABCD – параллелограмм (по признаку 1 0 )

2 0 . Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм

Дано: 1) ABCD -четырехугольник

2) ВС= А D , AB = CD .

Доказать, что ABCD – параллелограмм

Доказательство:

1) Дополнительное построение: диагональ АС

2) Рассмотрим АВС = СDА (по трем сторонам), так как

АС – общая сторона

АВ=СD, по условию

ВС=АD, по условию

3) Соответствующие элементы треугольников равны, тогда , но
- накрест лежащие углы при прямых AB и CD и секущей AC , значит AB || CD (по признаку параллельных прямых)

4) В четырехугольнике ABCD противолежащие стороны AB || CD , AB = CD , значит, ABCD – параллелограмм (по признаку 1 0 )

22.10.2014 Классная работа . Тема урока « », п. 43 I. «Рабочая тетрадь» 8 . В параллелограмме ABCD найдите: а) стороны, если ВС на 8 см больше стороны АВ, а периметр равен 64см; б)углы, если . 9 .В параллелограмме ABCD диагональАС,равная 24 см, образует со стороной AD угол 30°, O -точка пересечения диагоналейАСи BD , .Найдите длину отрезкаОЕ.
10 . Биссектриса угла А параллелограмма ABCD пересекает сторону ВС в точке Р, причем ВР=РС. Найдите стороны параллелограмма, если его периметр равен 54см.
11. Диагонали параллелограмма ABCD пересекаются в точке О. Периметр параллелограмма равен 12, а разность периметров РАВНА 2.Найдите стороны параллелограмма.
12. На рисунке в четырехугольнике ABCD .Докажите, что ABCD параллелограмм.

II . Атанасян , № 376 (б, д), 372 (а, б), 371 (б)

Задача 371(б) позволяет сделать вывод о виде выпуклого четырехугольника, значит, мы рассмотрели ПРИЗНАК ПАРАЛЛЕЛОГРАММА

III . ПРИЗНАКИ ПАРАЛЛЕЛОГРАММА (по презентации)

1 0 . Если в четырехугольнике _______________

___________________________________________ ,

то этот четырехугольник – ______________________ .

2 0 . Если в четырехугольнике ____________________

_______________________________________________ ,

то этот четырехугольник – ______________________

3 0 . Если в четырехугольнике ______________

_________________________________________

­­­­­­­­­­­­­­­­­­­­­­­­­­­____________________________,

то этот четырехугольник – ______________________ .

Домашнее задание для учащихся 8 класс 2016

Выучить теорию: п. 42, 43

Задачи: Базовый уровень: учебник(Атанасян) № 371 (а), 372 (в), 376 (в, г)

Повышенный уровень:

8. На рис. 121, ABCD – паралллелограмм, P MNKP = 20 см. Найдите MN , MP .

9. На рис.122 BNDM –паралллелограмм AB : BC =4:5, P ABCD = 18 см.Найдите AD , CD

1 0 . Если в четырехугольнике ___________________________________________________ _______________________________ , то этот четырехугольник – ___________________ . Дано: 1) ABCD -четырехугольник 2) АВ|| CD , AB = CD . Доказать, что ABCD – параллелограмм Доказательство:

1) Дополнительное построение:_____________________

Данный урок посвящён третьему признаку параллелограмма и его применению. На предыдущем уроке были изучены первый и второй признаки параллелограмма, которые основывались на свойствах сторон и углов параллелограмма. Третий признак основан на свойстве диагоналей параллелограмма. А именно, на том, что диагонали параллелограмма в точке пересечения делятся пополам. Признаки параллелограмма очень важны при решении целого ряда задач, поскольку позволяют доказывать то, что четырёхугольник является параллелограммом, а, значит, можно пользоваться его свойствами.

Тема: Четырехугольники

Урок: Третий признак параллелограмма

Напомним, что параллелограмм - это четырёхугольник, у которого противоположные стороны попарно параллельны. То есть, если - параллелограмм, то (см. Рис. 1).

Рис. 1

Параллелограмм обладает целым рядом свойств: противоположные углы равны (), противоположные стороны равны (). Кроме того, диагонали параллелограмма в точке пересечения делятся пополам, сумма углов, прилежащих к любой стороне параллелограмма, равна и т.д.

Но для того, чтобы пользоваться всеми этими свойствами, необходимо быть абсолютно уверенными в том, что рассматриваемый четырёхугольник - параллелограмм. Для этого и существуют признаки параллелограмма: то есть те факты, из которых можно сделать однозначный вывод, что четырёхугольник является параллелограммом. На предыдущем уроке мы уже рассмотрели два признака. Сейчас рассмотрим третий.

Если в четырёхугольнике диагонали в точке пересечения делятся пополам, то данный четырёхугольник является параллелограммом.

Дано:

Четырёхугольник; ; .

Доказать:

Параллелограмм.

Доказательство:

Для того чтобы доказать данный факт, необходимо доказать параллельность сторон параллелограмма. А параллельность прямых чаще всего доказывается через равенство внутренних накрест лежащих углов при этих прямых. Таким образом, напрашивается следующий способ доказательства третьего признака параллелограмма: через равенство треугольников .

Докажем равенство этих треугольников. Действительно, из условия следует: . Кроме того, поскольку углы - вертикальные, то они равны. То есть:

(первый признак равенства треугольников - по двум сторонам и углу между ними).

Из равенства треугольников: (так как равны внутренние накрест лежащие углы при этих прямых и секущей ). Кроме того, из равенства треугольников следует, что . Значит, мы получили, что в четырёхугольнике две стороны равны и параллельны. По первому признаку параллелограмма: - параллелограмм.

Доказано.

Рассмотрим пример на применение третьего признака параллелограмма.

Пример 1

Дано:

- параллелограмм; . - середина , - середина , - середина , - середина (см. Рис. 2).

Рис. 2

Доказать: - параллелограмм.

Доказательство:

Значит, в четырёхугольнике диагонали в точке пересечения делятся пополам. По третьему признаку параллелограмма из этого следует, что - параллелограмм.

Доказано.

Если провести анализ третьего признака параллелограмма, то можно заметить, что этот признак соответствует свойству параллелограмма. То есть, то, что диагонали делятся пополам, является не просто свойством параллелограмма, а его отличительным, характеристическим свойством, по которому его можно выделить из множества четырёхугольников.

На следующем уроке мы рассмотрим решение различных задач про параллелограмм.

Список литературы

1. Александров А.Д. и др. Геометрия, 8 класс. - М.: Просвещение, 2006.
2. Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия, 8 класс. - М.: Просвещение, 2011.
3. Мерзляк А.Г., Полонский В.Б., Якир С.М. Геометрия, 8 класс. - М.: ВЕНТАНА-ГРАФ, 2009.

1. Terver.ru ().
2. Фестиваль педагогических наук "Открытый урок" ().

Домашнее задание

Доказательство

Первым делом проведем диагональ AC . Получаются два треугольника: ABC и ADC .

Так как ABCD — параллелограмм, то справедливо следующее:

AD || BC \Rightarrow \angle 1 = \angle 2 как лежащие накрест.

AB || CD \Rightarrow \angle3 = \angle 4 как лежащие накрест.

Следовательно, \triangle ABC = \triangle ADC (по второму признаку: и AC — общая).

И, значит, \triangle ABC = \triangle ADC , то AB = CD и AD = BC .

Доказано!

2. Противоположные углы тождественны.

Доказательство

Согласно доказательству свойства 1 мы знаем, что \angle 1 = \angle 2, \angle 3 = \angle 4 . Таким образом сумма противоположных углов равна: \angle 1 + \angle 3 = \angle 2 + \angle 4 . Учитывая, что \triangle ABC = \triangle ADC получаем \angle A = \angle C , \angle B = \angle D .

Доказано!

3. Диагонали разделены пополам точкой пересечения.

Доказательство

Проведем еще одну диагональ.

По свойству 1 мы знаем, что противоположные стороны тождественны: AB = CD . Еще раз отметим накрест лежащие равные углы.

Таким образом видно, что \triangle AOB = \triangle COD по второму признаку равенства треугольников (два угла и сторона между ними). То есть, BO = OD (напротив углов \angle 2 и \angle 1 ) и AO = OC (напротив углов \angle 3 и \angle 4 соответственно).

Доказано!

Признаки параллелограмма

Если лишь один признак в вашей задаче присутствует, то фигура является параллелограммом и можно использовать, все свойства данной фигуры.

Для лучшего запоминания, заметим, что признак параллелограмма будет отвечать на следующий вопрос — «как узнать?» . То есть, как узнать, что заданная фигура это параллелограмм.

1. Параллелограммом является такой четырехугольник, у которого две стороны равны и параллельны.

AB = CD ; AB || CD \Rightarrow ABCD — параллелограмм.

Доказательство

Рассмотрим подробнее. Почему AD || BC ?

\triangle ABC = \triangle ADC по свойству 1 : AB = CD , AC — общая и \angle 1 = \angle 2 как накрест лежащие при параллельных AB и CD и секущей AC .

Но если \triangle ABC = \triangle ADC , то \angle 3 = \angle 4 (лежат напротив AB и CD соответственно). И следовательно AD || BC (\angle 3 и \angle 4 - накрест лежащие тоже равны).

Первый признак верен.

2. Параллелограммом является такой четырехугольник, у которого противоположные стороны равны.

AB = CD , AD = BC \Rightarrow ABCD — параллелограмм.

Доказательство

Рассмотрим данный признак. Еще раз проведем диагональ AC .

По свойству 1 \triangle ABC = \triangle ACD .

Из этого следует, что: \angle 1 = \angle 2 \Rightarrow AD || BC и \angle 3 = \angle 4 \Rightarrow AB || CD , то есть ABCD — параллелограмм.

Второй признак верен.

3. Параллелограммом является такой четырехугольник, у которого противоположные углы равны.

\angle A = \angle C , \angle B = \angle D \Rightarrow ABCD — параллелограмм.

Доказательство

2 \alpha + 2 \beta = 360^{\circ} (поскольку ABCD — четырехугольник, а \angle A = \angle C , \angle B = \angle D по условию).

Получается, \alpha + \beta = 180^{\circ} . Но \alpha и \beta являются внутренними односторонними при секущей AB .

И то, что \alpha + \beta = 180^{\circ} говорит и о том, что AD || BC .

При этом \alpha и \beta — внутренние односторонние при секущей AD . И это значит AB || CD .

Третий признак верен.

4. Параллелограммом является такой четырехугольник, у которого диагонали разделены точкой пересечения пополам.

AO = OC ; BO = OD \Rightarrow параллелограмм.

Доказательство

BO = OD ; AO = OC , \angle 1 = \angle 2 как вертикальные \Rightarrow \triangle AOB = \triangle COD , \Rightarrow \angle 3 = \angle 4 , и \Rightarrow AB || CD .

Аналогично BO = OD ; AO = OC , \angle 5 = \angle 6 \Rightarrow \triangle AOD = \triangle BOC \Rightarrow \angle 7 = \angle 8 , и \Rightarrow AD || BC .

Четвертый признак верен.

I. Если две противоположные стороны четырехугольника параллельны и равны, то этот четырехугольник - параллелограмм.

Задача 1. Из вершин В и D параллелограмма АBCD, у которого АВ≠ ВС и угол А — острый, проведены перпендикуляры BK и DM к прямой АС. Докажите, что четырехугольник BMDK — параллелограмм.

Доказательство.

Так как ВК и DM перпендикулярны одной и той же прямой АС, то ВК II DM. Кроме того, ВК и DM являются высотами, проведенными в равных треугольниках Δ АВС и Δ CDA из вершин равных углов ∠B и ∠D к одной и той же стороне АС, следовательно, ВК = DM. Имеем: две стороны ВК и DM четырехугольника BMDK параллельны и равны, значит, BMDK – параллелограмм, что и требовалось доказать.

II. Если противоположные стороны четырехугольника попарно равны, то этот четырехугольник — параллелограмм.

Задача 2. На сторонах AB, BC, CD и DA четырехугольника ABCD отмечены соответственно точки M, N, P и Q так, что AM=CP, BN=DQ, BM=DP, NC=QA. Докажите, что ABCD и MNPQ — параллелограммы.

Доказательство.

1. По условию в четырехугольнике ABCD противоположные стороны состоят из равных отрезков, поэтому равны, т.е. AD=BC, AB=CD. Следовательно, ABCD – параллелограмм.

2. Рассмотрим Δ MBN и Δ PDQ. BM=DP и BN=DQ по условию. ∠B =∠D как противолежащие углы параллелограмма ABCD. Значит, Δ MBN = Δ PDQ по двум сторонам и углу между ними (1-й признак равенства треугольников). А в равных треугольниках против равных углов лежат равные стороны. Отсюда MN=PQ. Мы доказали, что противоположные стороны MN и PQ четырехугольника MNPQ равны. Аналогично, из равенства треугольников Δ MAQ и Δ PCN следует равенство сторон MQ и PN, которые являются противоположными сторонами четырехугольника MNPQ. Имеем: противоположные стороны четырехугольника MNPQ попарно равны. Следовательно, четырехугольник MNPQ – параллелограмм. Задача решена.

III. Если диагонали четырехугольника пересекаются и точкой пересечения делятся пополам, то этот четырехугольник - параллелограмм.

Задача 3. Диагонали параллелограмма ABCD пересекаются в точке O, Докажите, что четырехугольник MNPQ, вершинами которого являются середины отрезков OA, OB, OC и OD, — параллелограмм.

Доказательство.

По свойству диагоналей параллелограмма ABCD его диагонали AC и BD точкой пересечения делятся пополам, т.е. ОА=ОС и ОВ=OD. Диагонали четырехугольника MNPQ так же пересекаются в точке О, которая будет серединой каждой их них. Действительно, так как вершины четырехугольника MNPQ по условию являются серединами отрезков ОА, ОС, ОВ и OD, то BN=ON=OQ=DQ и AM=OM=OP=CP. Следовательно, диагонали MP и NQ четырехугольника MNPQ в точке пересечения делятся пополам, следовательно, четырехугольник MNPQ – параллелограмм, что и требовалось доказать.

Понятие параллелограмма

Определение 1

Параллелограмм -- это четырехугольник, в котором противоположные стороны параллельны между собой (рис. 1).

Рисунок 1.

Параллелограмм имеет два основных свойства. Рассмотрим их без доказательства.

Свойство 1: Противоположные стороны и углы параллелограмма равны, соответственно, между собой.

Свойство 2: Диагонали, проведенные в параллелограмме, делятся пополам их точкой пересечения.

Признаки параллелограмма

Рассмотрим три признака параллелограмма и представим их в виде теорем.

Теорема 1

Если две стороны четырехугольника равны между собой, а также параллельны, то этот четырехугольник будет параллелограммом.

Доказательство.

Пусть нам дан четырехугольник $ABCD$. В котором $AB||CD$ и $AB=CD$ Проведем в нем диагональ $AC$ (рис. 2).

Рисунок 2.

Рассмотрим параллельные прямые $AB$ и $CD$ и их секущую $AC$. Тогда

\[\angle CAB=\angle DCA\]

как накрест лежащие углы.

По $I$ признаку равенства треугольников,

так как $AC$ -- их общая сторона, а $AB=CD$ по условию. Значит

\[\angle DAC=\angle ACB\]

Рассмотрим прямые $AD$ и $CB$ и их секущую $AC$, по последнему равенству накрест лежащих углов получим, что $AD||CB$.}Следовательно, по определению $1$, данный четырехугольник является параллелограммом.

Теорема доказана.

Теорема 2

Если противоположные стороны четырехугольника равны между собой, то он является параллелограммом.

Доказательство.

Пусть нам дан четырехугольник $ABCD$. В котором $AD=BC$ и $AB=CD$. Проведем в нем диагональ $AC$ (рис. 3).

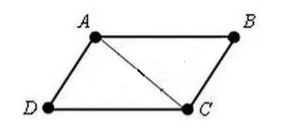
Рисунок 3.

Так как $AD=BC$, $AB=CD$, а $AC$ -- общая сторона, то по $III$ признаку равенства треугольников,

\[\triangle DAC=\triangle ACB\]

\[\angle DAC=\angle ACB\]

Рассмотрим прямые $AD$ и $CB$ и их секущую $AC$, по последнему равенству накрест лежащих углов получим, что $AD||CB$. Следовательно, по определению $1$, данный четырехугольник является параллелограммом.

\[\angle DCA=\angle CAB\]

Рассмотрим прямые $AB$ и $CD$ и их секущую $AC$, по последнему равенству накрест лежащих углов получим, что $AB||CD$. Следовательно, по определению 1, данный четырехугольник является параллелограммом.

Теорема доказана.

Теорема 3

Если диагонали, проведенные в четырехугольнике, своей точкой пересечения делятся на две равные части, то этот четырехугольник является параллелограммом.

Доказательство.

Пусть нам дан четырехугольник $ABCD$. Проведем в нем диагонали $AC$ и $BD$. Пусть они пересекаются в точке $O$ (рис. 4).

Рисунок 4.

Так как, по условию $BO=OD,\ AO=OC$, а углы $\angle COB=\angle DOA$ как вертикальные, то, по $I$ признаку равенства треугольников,

\[\triangle BOC=\triangle AOD\]

\[\angle DBC=\angle BDA\]

Рассмотрим прямые $BC$ и $AD$ и их секущую $BD$, по последнему равенству накрест лежащих углов получим, что $BC||AD$. Также $BC=AD$. Следовательно, по теореме $1$, данный четырехугольник является параллелограммом.