Возведение в степень произведение и частного. Степень и ее свойства. Исчерпывающий гид (2020) Что такое степень произведения

Возведение в степень – операция, тесно связанная с умножением, это операция – результат многократного умножения какого-либо числа на само себя. Изобразим формулой: a1 * a2 * … * an = an .

Например, а=2, n=3: 2 * 2 * 2=2^3 = 8 .

Вообще возведение в степень часто используется в различных формулах по математике и физике. Эта функция имеет более научное предназначение, чем четыре основные: Сложение , Вычитание , Умножение , Деление .

Возведение числа в степень

Возведение числа в степень – операция не сложная. Оно связано с умножением подобно связи умножения и сложения. Запись an – краткая запись n-ого количество чисел «а» умноженных друг на друга.

Рассмотри возведение в степень на самых простых примерах, переходя к сложным.

Например, 42. 42 = 4 * 4 = 16 . Четыре в квадрате (во второй степени) равно шестнадцати. Если вам не понятно умножение 4 * 4 , то читайте нашу стать об умножении .

Рассмотрим еще одни пример: 5^3. 5^3 = 5 * 5 * 5 = 25 * 5 = 125 . Пять в кубе (в третьей степени) равно ста двадцати пяти.

Еще один пример: 9^3. 9^3 = 9 * 9 * 9 = 81 * 9 = 729 . Девять в кубе равняется семи сотням двадцати девяти.

Формулы возведения в степень

Чтобы грамотно возводить в степень нужно помнить и знать формулы, указанные ниже. В этом нет ничего сверх естественного, главное понять суть и тогда они не только запомнятся, но и покажутся легкими.

Возведение одночлена в степень

Что из себя представляет одночлен? Это произведение чисел и переменных в любом количестве. Например, двух – одночлен. И вот именно о возведении в степень таких одночленов данная статья.

Пользуясь формулами возведения в степень вычислить возведение одночлена в степень будет не трудно.

Например, (3x^2y^3)^2= 3^2 * x^2 * 2 * y^(3 * 2) = 9x^4y^6 ; Если возводить одночлен в степень, то в степень возводится каждая составная одночлена.

Возводя в степень переменную уже имеющую степень, то степени перемножаются. Например, (x^2)^3 = x^(2 * 3) = x^6 ;

Возведение в отрицательную степень

Отрицательная степень – обратное число. Что такое обратное число? Любому числу Х обратным будет 1/X. То есть Х-1=1/X. Это и есть суть отрицательной степени.

Рассмотрим пример (3Y)^-3:

(3Y)^-3 = 1/(27Y^3).

Почему так? Так как в степени имеется минус, то просто переносим в знаменатель данное выражение, а затем возводим в его в третью степень. Просто не так ли?

Возведение в дробную степень

Начнем рассмотрение вопрос на конкретном примере. 43/2. Что означает степень 3/2? 3 – числитель, означает возведение числа (в данном случае 4) в куб. Число 2 – знаменатель, это извлечение корня второй степени из числа (в данном случае 4).

Тогда получаем квадратный корень из 43 = 2^3 = 8 . Ответ: 8.

Итак, знаменатель дробной степени может быть, как 3, так и 4 и до бесконечности любым числом и это число определяет степень квадратного корня, извлекаемого из заданного числа. Конечно же, знаменатель не может быть равным нулю.

Возведение корня в степень

Если корень возводится в степень, равной степени самого корня, то ответом будет подкоренное выражение. Например, (√х)2 = х. И так в любом случае равенства степени корня и степени возведения корня.

Если (√x)^4. То (√x)^4=x^2. Чтобы проверить решение переведем выражение в выражение с дробной степенью. Так как корень квадратный, то знаменатель равен 2. А если корень возводится в четвертую степень, то числитель 4. Получаем 4/2=2. Ответ: x = 2.

В любом случае лучший вариант просто перевести выражение в выражение с дробной степенью. Если не будет сокращаться дробь, значит такой ответ и будет, при условии, что корень из заданного числа не выделяется.

Возведение в степень комплексного числа

Что такое комплексное число? Комплексное число – выражение, имеющее формулу a + b * i; a, b – действительные числа. i – число, которое при возведение в квадрат дает число -1.

Рассмотрим пример. (2 + 3i)^2.

(2 + 3i)^2 = 22 +2 * 2 * 3i +(3i)^2 = 4+12i^-9=-5+12i.

Запишитесь на курс "Ускоряем устный счет, НЕ ментальная арифметика", чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.

Возведение в степень онлайн

С помощью нашего калькулятора, Вы сможете посчитать возведение числа в степень:

Возведение в степень 7 класс

Возведение в степень начинают проходить школьники только в седьмом классе.

Возведение в степень – операция, тесно связанная с умножением, это операция – результат многократного умножения какого-либо числа на само себя. Изобразим формулой: a1 * a2 * … * an=an .

Например, а=2, n=3: 2 * 2 * 2 = 2^3 = 8 .

Примеры для решения:

Возведение в степень презентация

Презентация по возведению в степень, рассчитанную на семиклассников. Презентация может разъяснить некоторые непонятные моменты, но, вероятно, таких моментов не будет благодаря нашей статье.

Итог

Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше - записывайтесь на наш курс: Ускоряем устный счет - НЕ ментальная арифметика.

Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.

Формулы степеней используют в процессе сокращения и упрощения сложных выражений, в решении уравнений и неравенств.

Число c является n -ной степенью числа a когда:

Операции со степенями.

1. Умножая степени с одинаковым основанием их показатели складываются:

a m ·a n = a m + n .

2. В делении степеней с одинаковым основанием их показатели вычитаются:

3. Степень произведения 2-х либо большего числа множителей равняется произведению степеней этих сомножителей:

(abc…) n = a n · b n · c n …

4. Степень дроби равняется отношению степеней делимого и делителя:

(a/b) n = a n /b n .

5. Возводя степень в степень, показатели степеней перемножают:

(a m) n = a m n .

Каждая вышеприведенная формула верна в направлениях слева направо и наоборот.

Например . (2·3·5/15)² = 2²·3²·5²/15² = 900/225 = 4 .

Операции с корнями.

1. Корень из произведения нескольких сомножителей равняется произведению корней из этих сомножителей:

2. Корень из отношения равен отношению делимого и делителя корней:

3. При возведении корня в степень довольно возвести в эту степень подкоренное число:

4. Если увеличить степень корня в n раз и в тоже время возвести в n -ую степень подкоренное число, то значение корня не поменяется:

5. Если уменьшить степень корня в n раз и в тоже время извлечь корень n -ой степени из подкоренного числа, то значение корня не поменяется:

Степень с отрицательным показателем. Степень некоторого числа с неположительным (целым) показателем определяют как единицу, деленную на степень того же числа с показателем, равным абсолютной величине неположительного показателя:

Формулу a m :a n =a m - n можно использовать не только при m > n , но и при m < n .

Например . a 4:a 7 = a 4 - 7 = a -3 .

Чтобы формула a m :a n =a m - n стала справедливой при m=n , нужно присутствие нулевой степени.

Степень с нулевым показателем. Степень всякого числа, не равного нулю, с нулевым показателем равняется единице.

Например . 2 0 = 1,(-5) 0 = 1,(-3/5) 0 = 1.

Степень с дробным показателем. Чтобы возвести действительное число а в степень m/n , необходимо извлечь корень n -ой степени из m -ой степени этого числа а .

Напоминаем, что в данном уроке разбираются свойства степеней с натуральными показателями и нулём. Степени с рациональными показателями и их свойства будут рассмотрены в уроках для 8 классов.

Степень с натуральным показателем обладает несколькими важными свойствами, которые позволяют упрощать вычисления в примерах со степенями.

Свойство № 1
Произведение степеней

Запомните!

При умножении степеней с одинаковыми основаниями основание остаётся без изменений, а показатели степеней складываются.

a m · a n = a m + n , где «a » — любое число, а «m », «n » — любые натуральные числа.

Данное свойство степеней также действует на произведение трёх и более степеней.

• Упростить выражение.
  b · b 2 · b 3 · b 4 · b 5 = b 1 + 2 + 3 + 4 + 5 = b 15
• Представить в виде степени.
  6 15 · 36 = 6 15 · 6 2 = 6 15 · 6 2 = 6 17
• Представить в виде степени.
  (0,8) 3 · (0,8) 12 = (0,8) 3 + 12 = (0,8) 15

Важно!

Обратите внимание, что в указанном свойстве речь шла только об умножении степеней с одинаковыми основаниями . Оно не относится к их сложению.

Нельзя заменять сумму (3 3 + 3 2) на 3 5 . Это понятно, если
посчитать (3 3 + 3 2) = (27 + 9) = 36 , а 3 5 = 243

Свойство № 2
Частное степеней

Запомните!

При делении степеней с одинаковыми основаниями основание остаётся без изменений, а из показателя степени делимого вычитают показатель степени делителя.

= 11 3 − 2 · 4 2 − 1 = 11 · 4 = 44

Пример. Решить уравнение. Используем свойство частного степеней.
3 8: t = 3 4

T = 3 8 − 4

Ответ: t = 3 4 = 81

Пользуясь свойствами № 1 и № 2, можно легко упрощать выражения и производить вычисления.

• Пример. Упростить выражение.
  4 5m + 6 · 4 m + 2: 4 4m + 3 = 4 5m + 6 + m + 2: 4 4m + 3 = 4 6m + 8 − 4m − 3 = 4 2m + 5
• Пример. Найти значение выражения, используя свойства степени.
  = = = 2 9 + 2

  2 5

  = 2 11

  2 5

  = 2 11 − 5 = 2 6 = 64

  Важно!

  Обратите внимание, что в свойстве 2 речь шла только о делении степеней с одинаковыми основаниями.

  Нельзя заменять разность (4 3 −4 2) на 4 1 . Это понятно, если посчитать (4 3 −4 2) = (64 − 16) = 48 , а 4 1 = 4

  Будьте внимательны!

  Свойство № 3
  Возведение степени в степень

  Запомните!

  При возведении степени в степень основание степени остаётся без изменения, а показатели степеней перемножаются.

  (a n) m = a n · m , где «a » — любое число, а «m », «n » — любые натуральные числа.

  
  

  Свойства 4
  Степень произведения

  Запомните!

  При возведении в степень произведения каждый из множителей возводится в степень. Затем полученные результаты перемножаются.

  (a · b) n = a n · b n , где «a », «b » — любые рациональные числа; «n » — любое натуральное число.

  • Пример 1.
    (6 · a 2 · b 3 · c) 2 = 6 2 · a 2 · 2 · b 3 · 2 · с 1 · 2 = 36 a 4 · b 6 · с 2
    
  • Пример 2.
    (−x 2 · y) 6 = ((−1) 6 · x 2 · 6 · y 1 · 6) = x 12 · y 6

  Важно!

  Обратите внимание, что свойство № 4, как и другие свойства степеней, применяют и в обратном порядке.

  (a n · b n)= (a · b) n

  То есть, чтобы перемножить степени с одинаковыми показателями можно перемножить основания, а показатель степени оставить неизменным.

  • Пример. Вычислить.
    2 4 · 5 4 = (2 · 5) 4 = 10 4 = 10 000
  • Пример. Вычислить.
    0,5 16 · 2 16 = (0,5 · 2) 16 = 1

  В более сложных примерах могут встретиться случаи, когда умножение и деление надо выполнить над степенями с разными основаниями и разными показателями. В этом случае советуем поступать следующим образом.

  Например, 4 5 · 3 2 = 4 3 · 4 2 · 3 2 = 4 3 · (4 · 3) 2 = 64 · 12 2 = 64 · 144 = 9216
  

  Пример возведения в степень десятичной дроби.

  4 21 · (−0,25) 20 = 4 · 4 20 · (−0,25) 20 = 4 · (4 · (−0,25)) 20 = 4 · (−1) 20 = 4 · 1 = 4

  Свойства 5
  Степень частного (дроби)

  Запомните!

  Чтобы возвести в степень частное, можно возвести в эту степень отдельно делимое и делитель, и первый результат разделить на второй.

  (a: b) n = a n: b n , где «a », «b » — любые рациональные числа, b ≠ 0, n — любое натуральное число.

  • Пример. Представить выражение в виде частного степеней.
    (5: 3) 12 = 5 12: 3 12

  Напоминаем, что частное можно представить в виде дроби. Поэтому на теме возведение дроби в степень мы остановимся более подробно на следующей странице.

Мы разобрались, что вообще из себя представляет степень числа. Теперь нам надо понять, как правильно выполнять ее вычисление, т.е. возводить числа в степень. В этом материале мы разберем основные правила вычисления степени в случае целого, натурального, дробного, рационального и иррационального показателя. Все определения будут проиллюстрированы примерами.

Понятие возведения в степень

Начнем с формулирования базовых определений.

Определение 1

Возведение в степень - это вычисление значения степени некоторого числа.

То есть слова "вычисление значение степени" и "возведение в степень" означают одно и то же. Так, если в задаче стоит "Возведите число 0 , 5 в пятую степень", это следует понимать как "вычислите значение степени (0 , 5) 5 .

Теперь приведем основные правила, которым нужно придерживаться при таких вычислениях.

Вспомним, что такое степень числа с натуральным показателем. Для степени с основанием a и показателем n это будет произведение n -ного числа множителей, каждый из которых равен a . Это можно записать так:

Чтобы вычислить значение степени, нужно выполнить действие умножения, то есть перемножить основания степени указанное число раз. На умении быстро умножать и основано само понятие степени с натуральным показателем. Приведем примеры.

Пример 1

Условие: возведите - 2 в степень 4 .

Решение

Используя определение выше, запишем: (− 2) 4 = (− 2) · (− 2) · (− 2) · (− 2) . Далее нам нужно просто выполнить указанные действия и получить 16 .

Возьмем пример посложнее.

Пример 2

Вычислите значение 3 2 7 2

Решение

Данную запись можно переписать в виде 3 2 7 · 3 2 7 . Ранее мы рассматривали, как правильно умножать смешанные числа, упомянутые в условии.

Выполним эти действия и получим ответ: 3 2 7 · 3 2 7 = 23 7 · 23 7 = 529 49 = 10 39 49

Если в задаче указана необходимость возводить иррациональные числа в натуральную степень, нам потребуется предварительно округлить их основания до разряда, который позволит нам получить ответ нужной точности. Разберем пример.

Пример 3

Выполните возведение в квадрат числа π .

Решение

Для начала округлим его до сотых. Тогда π 2 ≈ (3 , 14) 2 = 9 , 8596 . Если же π ≈ 3 . 14159 , то мы получим более точный результат: π 2 ≈ (3 , 14159) 2 = 9 , 8695877281 .

Отметим, что необходимость высчитывать степени иррациональных чисел на практике возникает сравнительно редко. Мы можем тогда записать ответ в виде самой степени (ln 6) 3 или преобразовать, если это возможно: 5 7 = 125 5 .

Отдельно следует указать, что такое первая степень числа. Тут можно просто запомнить, что любое число, возведенное в первую степень, останется самим собой:

Это понятно из записи .

От основания степени это не зависит.

Пример 4

Так, (− 9) 1 = − 9 , а 7 3 , возведенное в первую степень, останется равно 7 3 .

Для удобства разберем отдельно три случая: если показатель степени - целое положительное число, если это ноль и если это целое отрицательное число.

В первое случае это то же самое, что и возведение в натуральную степень: ведь целые положительные числа принадлежат ко множеству натуральных. О том, как работать с такими степенями, мы уже рассказали выше.

Теперь посмотрим, как правильно возводить в нулевую степень. При основании, которое отличается от нуля, это вычисление всегда дает на выходе 1 . Ранее мы уже поясняли, что 0 -я степень a может быть определена для любого действительного числа, не равного 0 , и a 0 = 1 .

Пример 5

5 0 = 1 , (- 2 , 56) 0 = 1 2 3 0 = 1

0 0 - не определен.

У нас остался только случай степени с целым отрицательным показателем. Мы уже разбирали, что такие степени можно записать в виде дроби 1 a z , где а - любое число, а z - целый отрицательный показатель. Мы видим, что знаменатель этой дроби есть не что иное, как обыкновенная степень с целым положительным показателем, а ее вычислять мы уже научились. Приведем примеры задач.

Пример 6

Возведите 2 в степень - 3 .

Решение

Используя определение выше, запишем: 2 - 3 = 1 2 3

Подсчитаем знаменатель этой дроби и получим 8: 2 3 = 2 · 2 · 2 = 8 .

Тогда ответ таков: 2 - 3 = 1 2 3 = 1 8

Пример 7

Возведите 1 , 43 в степень - 2 .

Решение

Переформулируем: 1 , 43 - 2 = 1 (1 , 43) 2

Вычисляем квадрат в знаменателе: 1,43·1,43. Десятичные дроби можно умножить таким способом: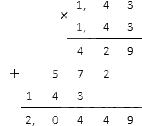

В итоге у нас вышло (1 , 43) - 2 = 1 (1 , 43) 2 = 1 2 , 0449 . Этот результат нам осталось записать в виде обыкновенной дроби, для чего необходимо умножить ее на 10 тысяч (см. материал о преобразовании дробей).

Ответ: (1 , 43) - 2 = 10000 20449

Отдельный случай - возведение числа в минус первую степень. Значение такой степени равно числу, обратному исходному значению основания: a - 1 = 1 a 1 = 1 a .

Пример 8

Пример: 3 − 1 = 1 / 3

9 13 - 1 = 13 9 6 4 - 1 = 1 6 4 .

Как возвести число в дробную степень

Для выполнения такой операции нам потребуется вспомнить базовое определение степени с дробным показателем: a m n = a m n при любом положительном a , целом m и натуральном n .

Определение 2

Таким образом, вычисление дробной степени нужно выполнять в два действия: возведение в целую степень и нахождение корня n -ной степени.

У нас есть равенство a m n = a m n , которое, учитывая свойства корней, обычно применяется для решения задач в виде a m n = a n m . Это значит, что если мы возводим число a в дробную степень m / n , то сначала мы извлекаем корень n -ной степени из а, потом возводим результат в степень с целым показателем m .

Проиллюстрируем на примере.

Пример 9

Вычислите 8 - 2 3 .

Решение

Способ 1. Согласно основному определению, мы можем представить это в виде: 8 - 2 3 = 8 - 2 3

Теперь подсчитаем степень под корнем и извлечем корень третьей степени из результата: 8 - 2 3 = 1 64 3 = 1 3 3 64 3 = 1 3 3 4 3 3 = 1 4

Способ 2. Преобразуем основное равенство: 8 - 2 3 = 8 - 2 3 = 8 3 - 2

После этого извлечем корень 8 3 - 2 = 2 3 3 - 2 = 2 - 2 и результат возведем в квадрат: 2 - 2 = 1 2 2 = 1 4

Видим, что решения идентичны. Можно пользоваться любым понравившимся способом.

Бывают случаи, когда степень имеет показатель, выраженный смешанным числом или десятичной дробью. Для простоты вычислений его лучше заменить обычной дробью и считать, как указано выше.

Пример 10

Возведите 44 , 89 в степень 2 , 5 .

Решение

Преобразуем значение показателя в обыкновенную дробь: 44 , 89 2 , 5 = 44 , 89 5 2 .

А теперь выполняем по порядку все действия, указанные выше: 44 , 89 5 2 = 44 , 89 5 = 44 , 89 5 = 4489 100 5 = 4489 100 5 = 67 2 10 2 5 = 67 10 5 = = 1350125107 100000 = 13 501 , 25107

Ответ: 13 501 , 25107 .

Если в числителе и знаменателе дробного показателя степени стоят большие числа, то вычисление таких степеней с рациональными показателями - довольно сложная работа. Для нее обычно требуется вычислительная техника.

Отдельно остановимся на степени с нулевым основанием и дробным показателем. Выражению вида 0 m n можно придать такой смысл: если m n > 0 , то 0 m n = 0 m n = 0 ; если m n < 0 нуль остается не определен. Таким образом, возведение нуля в дробную положительную степень приводит к нулю: 0 7 12 = 0 , 0 3 2 5 = 0 , 0 0 , 024 = 0 , а в целую отрицательную - значения не имеет: 0 - 4 3 .

Как возвести число в иррациональную степень

Необходимость вычислить значение степени, в показателе которой стоит иррациональное число, возникает не так часто. На практике обычно задача ограничивается вычислением приблизительного значения (до некоторого количества знаков после запятой). Обычно это считают на компьютере из-за сложности таких подсчетов, поэтому подробно останавливаться на этом не будем, укажем лишь основные положения.

Если нам нужно вычислить значение степени a с иррациональным показателем a , то мы берем десятичное приближение показателя и считаем по нему. Результат и будет приближенным ответом. Чем точнее взятое десятичное приближение, тем точнее ответ. Покажем на примере:

Пример 11

Вычислите приближенное значение 2 в степени 1,174367....

Решение

Ограничимся десятичным приближением a n = 1 , 17 . Проведем вычисления с использованием этого числа: 2 1 , 17 ≈ 2 , 250116 . Если же взять, к примеру, приближение a n = 1 , 1743 , то ответ будет чуть точнее: 2 1 , 174367 . . . ≈ 2 1 , 1743 ≈ 2 , 256833 .

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Основная цель

Ознакомить учащихся со свойствами степеней с натуральными показателями и научить выполнять действия со степенями.

Тема “ Степень и её свойства ” включает три вопроса:

• Определение степени с натуральным показателем.
• Умножение и деление степеней.
• Возведение в степень произведения и степени.

Контрольные вопросы

1. Сформулируйте определение степени с натуральным показателем, большим 1. Приведите пример.
2. Сформулируйте определение степени с показателем 1. Приведите пример.
3. Каков порядок выполнения действий при вычислении значения выражения, содержащего степени?
4. Сформулируйте основное свойство степени. Приведите пример.
5. Сформулируйте правило умножения степеней с одинаковыми основаниями. Приведите пример.
6. Сформулируйте правило деления степеней с одинаковыми основаниями. Приведите пример.
7. Сформулируйте правило возведения в степень произведения. Приведите пример. Докажите тождество (ab) n = a n b n .
8. Сформулируйте правило возведения степени в степень. Приведите пример. Докажите тождество (а m) n = а m n .

Определение степени.

Степенью числа a с натуральным показателем n , большим 1, называется произведение n множителей, каждый из которых равен а . Степенью числа а с показателем 1 называется само число а .

Степень с основанием а и показателем n записывается так: а n . Читается “ а в степени n ”; “ n- я степень числа а ”.

По определению степени:

а 4 = а а а а

. . . . . . . . . . . .

Нахождение значения степени называют возведением в степень .

1. Примеры возведения в степень:

3 3 = 3 3 3 = 27

0 4 = 0 0 0 0 = 0

(-5) 3 = (-5) (-5) (-5) = -125

25 ; 0,09 ;

25 = 5 2 ; 0,09 = (0,3) 2 ; .

27 ; 0,001 ; 8 .

27 = 3 3 ; 0,001 = (0,1) 3 ; 8 = 2 3 .

4. Найти значения выражений:

а) 3 10 3 = 3 10 10 10 = 3 1000 = 3000

б) -2 4 + (-3) 2 = 7
2 4 = 16
(-3) 2 = 9
-16 + 9 = 7

Вариант 1

а) 0,3 0,3 0,3

в) b b b b b b b

г) (-х) (-х) (-х) (-х)

д) (ab) (ab) (ab)

2. Представьте в виде квадрата числа:

3. Представьте в виде куба числа:

4. Найти значения выражений:

в) -1 4 + (-2) 3

г) -4 3 + (-3) 2

д) 100 - 5 2 4

Умножение степеней.

Для любого числа а и произвольных чисел m и n выполняется:

a m a n = a m + n .

Доказательство:

Правило : При умножении степеней с одинаковыми основаниями основания оставляют прежним, а показатели степеней складывают.

a m a n a k = a m + n a k = a (m + n) + k = a m + n + k

а) х 5 х 4 = х 5 + 4 = х 9

б) y y 6 = y 1 y 6 = y 1 + 6 = y 7

в) b 2 b 5 b 4 = b 2 + 5 + 4 = b 11

г) 3 4 9 = 3 4 3 2 = 3 6

д) 0,01 0,1 3 = 0,1 2 0,1 3 = 0,1 5

а) 2 3 2 = 2 4 = 16

б) 3 2 3 5 = 3 7 = 2187

Вариант 1

1. Представить в виде степени:

а) х 3 х 4 е) х 2 х 3 х 4

б) а 6 а 2 ж) 3 3 9

в) у 4 у з) 7 4 49

г) а а 8 и) 16 2 7

д) 2 3 2 4 к) 0,3 3 0,09

2. Представить в виде степени и найти значение по таблице:

а) 2 2 2 3 в) 8 2 5

б) 3 4 3 2 г) 27 243

Деление степеней.

Для любого числа а0 и произвольных натуральных чисел m и n, таких, что m>n выполняется:

a m: a n = a m - n

Доказательство:

a m - n a n = a (m - n) + n = a m - n + n = a m

по определению частного:

a m: a n = a m - n .

Правило : При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.

Определение: Степень числа а, не равного нулю, с нулевым показателем равна единице :

т.к. а n: a n = 1 при а0 .

а) х 4:х 2 = х 4 - 2 = х 2

б) у 8:у 3 = у 8 - 3 = у 5

в) а 7:а = а 7:а 1 = а 7 - 1 = а 6

г) с 5:с 0 = с 5:1 = с 5

а) 5 7:5 5 = 5 2 = 25

б) 10 20:10 17 = 10 3 = 1000

в)

г)

д)

Вариант 1

1. Представьте в виде степени частное:

2. Найдите значения выражений:

Возведение в степень произведения.

Для любых а и b и произвольного натурального числа n:

(ab) n = a n b n

Доказательство:

По определению степени

(ab) n =

Сгруппировав отдельно множители а и множители b, получим:

=

Доказанное свойство степени произведения распространяется на степень произведения трех и более множителей.

Например:

(a b c) n = a n b n c n ;

(a b c d) n = a n b n c n d n .

Правило : При возведении в степень произведения возводят в эту степень каждый множитель и результат перемножают.

1. Возвести в степень:

а) (a b) 4 = a 4 b 4

б) (2 х у) 3 =2 3 х 3 у 3 = 8 х 3 у 3

в) (3 а) 4 = 3 4 а 4 = 81 а 4

г) (-5 у) 3 = (-5) 3 у 3 = -125 у 3

д) (-0,2 х у) 2 = (-0,2) 2 х 2 у 2 = 0,04 х 2 у 2

е) (-3 a b c) 4 = (-3) 4 a 4 b 4 c 4 = 81 a 4 b 4 c 4

2. Найти значение выражения:

а) (2 10) 4 = 2 4 10 4 = 16 1000 = 16000

б) (3 5 20) 2 = 3 2 100 2 = 9 10000= 90000

в) 2 4 5 4 = (2 5) 4 = 10 4 = 10000

г) 0,25 11 4 11 = (0,25 4) 11 = 1 11 = 1

д)

Вариант 1

1. Возвести в степень:

б) (2 а с) 4

д) (-0,1 х у) 3

2. Найти значение выражения:

б) (5 7 20) 2

Возведение в степень степени.

Для любого числа а и произвольных натуральных чисел m и n:

(а m) n = а m n

Доказательство:

По определению степени

(а m) n =

Правило: При возведении степени в степень основание оставляют тем же, а показатели перемножают .

1. Возвести в степень:

(а 3) 2 = а 6 (х 5) 4 = х 20

(у 5) 2 = у 10 (b 3) 3 = b 9

2. Упростите выражения:

а) а 3 (а 2) 5 = а 3 а 10 = а 13

б) (b 3) 2 b 7 = b 6 b 7 = b 13

в) (х 3) 2 (х 2) 4 = х 6 х 8 = х 14

г) (у у 7) 3 = (у 8) 3 = у 24

а)

б)

Вариант 1

1. Возвести в степень:

а) (а 4) 2 б) (х 4) 5

в) (у 3) 2 г) (b 4) 4

2. Упростите выражения:

а) а 4 (а 3) 2

б) (b 4) 3 b 5+

в) (х 2) 4 (х 4) 3

г) (у у 9) 2

3. Найдите значение выражений:

Приложение

Определение степени.

Вариант 2

1ю Запишите произведение в виде степени:

а) 0,4 0,4 0,4

в) а а а а а а а а

г) (-у) (-у) (-у) (-у)

д) (bс) (bс) (bс)

2. Представьте в виде квадрата числа:

3. Представьте в виде куба числа:

4. Найти значения выражений:

в) -1 3 + (-2) 4

г) -6 2 + (-3) 2

д) 4 5 2 – 100

Вариант 3

1. Запишите произведение в виде степени:

а) 0,5 0,5 0,5

в) с с с с с с с с с

г) (-х) (-х) (-х) (-х)

д) (ab) (ab) (ab)

2. Представьте в виде квадрата числа: 100 ; 0,49 ; .

3. Представьте в виде куба числа:

4. Найти значения выражений:

в) -1 5 + (-3) 2

г) -5 3 + (-4) 2

д) 5 4 2 - 100

Вариант 4

1. Запишите произведение в виде степени:

а) 0,7 0,7 0,7

в) х х х х х х

г) (-а) (-а) (-а)

д) (bс) (bс) (bс) (bc)

2. Представьте в виде квадрата числа:

3. Представьте в виде куба числа:

4. Найти значения выражений:

в) -1 4 + (-3) 3

г) -3 4 + (-5) 2

д) 100 - 3 2 5

Умножение степеней.

Вариант 2

1. Представить в виде степени:

а) х 4 x 5 е) х 3 х 4 х 5

б) а 7 а 3 ж) 2 3 4

в) у 5 у з) 4 3 16

г) а а 7 и) 4 2 5

д) 2 2 2 5 к) 0,2 3 0,04

2. Представить в виде степени и найти значение по таблице:

а) 3 2 3 3 в) 16 2 3

б) 2 4 2 5 г) 9 81

Вариант 3

1. Представить в виде степени:

а) а 3 а 5 е) у 2 у 4 у 6

б) х 4 х 7 ж) 3 5 9

в) b 6 b з) 5 3 25

г) у у 8 и) 49 7 4

д) 2 3 2 6 к) 0,3 4 0,27

2. Представить в виде степени и найти значение по таблице:

а) 3 3 3 4 в) 27 3 4

б) 2 4 2 6 г) 16 64

Вариант 4

1. Представить в виде степени:

а) а 6 а 2 е) х 4 х х 6

б) х 7 х 8 ж) 3 4 27

в) у 6 у з) 4 3 16

г) х х 10 и) 36 6 3

д) 2 4 2 5 к) 0,2 2 0,008

2. Представить в виде степени и найти значение по таблице:

а) 2 6 2 3 в) 64 2 4

б) 3 5 3 2 г) 81 27

Деление степеней.

Вариант 2

1. Представьте в виде степени частное:

2. Найдите значения выражений: