Статистическая значимость формула. Какими бывают ошибки? Какие уровни значимости используются

Статистика давно уже стала неотъемлемой частью жизни. С ней люди сталкиваются всюду. На основе статистики делаются выводы о том, где и какие заболевания распространены, что более востребовано в конкретном регионе или среди определенного слоя населения. На основываются даже построения политических программ кандидатов в органы власти. Ими же пользуются и торговые сети при закупке товаров, а производители руководствуются этими данными в своих предложениях.

Статистика играет важную роль в жизни общества и влияет на каждого его отдельного члена даже в мелочах. Например, если по , большинство людей предпочитают темные цвета в одежде в конкретном городе или регионе, то найти яркий желтый плащ с цветочным принтом в местных торговых точках будет крайне затруднительно. Но из каких величин складываются эти данные, оказывающие такое влияние? К примеру, что представляет собой «статистическая значимость»? Что именно понимается под этим определением?

Что это?

Статистика как наука складывается из сочетания разных величин и понятий. Одним из них и является понятие «статистическая значимость». Так называется значение переменных величин, вероятность появления других показателей в которых ничтожно мала.

К примеру, 9 из 10 человек надевают на ноги резиновую обувь во время утренней прогулки за грибами в осенний лес после дождливой ночи. Вероятность того что в какой-то момент 8 из них обуются в парусиновые мокасины - ничтожно мала. Таким образом, в данном конкретном примере число 9 является величиной, которая и называется «статистическая значимость».

Соответственно, если развивать далее приведенный практический пример, обувные магазины закупают к концу летнего сезона резиновые сапожки в большом количестве, чем в другое время года. Так, величина статистического значения оказывает влияние на обычную жизнь.

Разумеется, в сложных подсчетах, допустим, при прогнозе распространения вирусов, учитывается большое число переменных. Но сама суть определения значимого показателя статистических данных - аналогична, вне зависимости от сложности подсчетов и количества непостоянных величин.

Как вычисляют?

Используются при вычислении значения показателя «статистическая значимость» уравнения. То есть можно утверждать, что в этом случае все решает математика. Самым простым вариантом вычисления является цепь математических действий, в которой участвуют следующие параметры:

• два типа результатов, полученных при опросах или изучении объективных данных, к примеру, сумм на которые совершаются покупки, обозначаемые а и b;
• показатель для обеих групп - n;
• значение доли объединенной выборки - p;
• понятие «стандартная ошибка» - SE.

Следующим этапом определяется общий тестовый показатель - t, его значение сравнивается с числом 1,96. 1,96 - это усредненное значение, передающее диапазон в 95 %, согласно функции t-распределения Стьюдента.

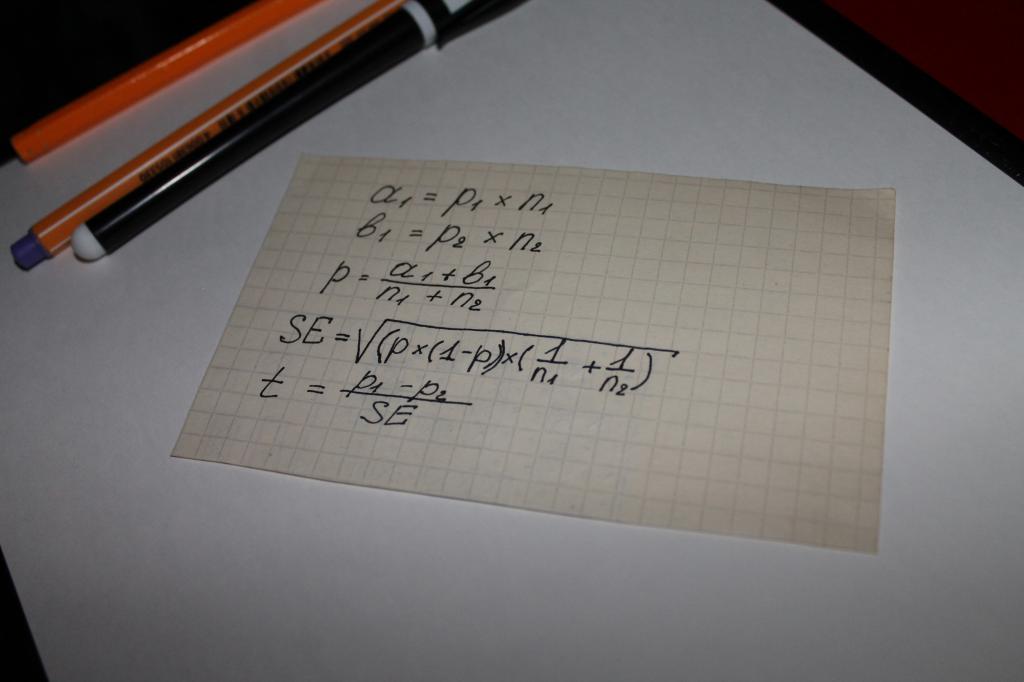
Часто возникает вопрос о том, в чем отличие значений n и p. Этот нюанс просто прояснить при помощи примера. Допустим, вычисляется статистическая значимость лояльности к какому-либо товару или бренду мужчин и женщин.

В этом случае за буквенными обозначениями будет стоять следующее:

• n - число опрошенных;
• p - число довольных продуктом.

Численность опрошенных женщин в этом случае будет обозначено, как n1. Соответственно, мужчин - n2. То же значение будут иметь цифры «1» и «2» у символа p.

Сравнение тестового показателя с усредненными значениями расчетных таблиц Стьюдента и становится тем, что называется «статистическая значимость».

Что понимается под проверкой?

Результаты любого математического вычисления всегда можно проверить, этому учат детей еще в начальных классах. Логично предположить, что раз статистические показатели определяются при помощи цепи вычислений, то и проверяются.

Однако проверка статистической значимости - не только математика. Статистика имеет дело с большим количеством переменных величин и различных вероятностей, далеко не всегда поддающихся расчету. То есть если вернутся к приведенному в начале статьи примеру с резиновой обувью, то логичное построение статистических данных, на которые станут опираться закупщики товаров для магазинов, может быть нарушено сухой и жаркой погодой, которая не типична для осени. В результате этого явления число людей, приобретающих резиновые сапоги, снизится, а торговые точки потерпят убытки. Предусмотреть погодную аномалию математическая формула, разумеется, не в состоянии. Этот момент называется - «ошибка».

Вот как раз вероятность таких ошибок и учитывает проверка уровня вычисленной значимости. В ней учитываются как вычисленные показатели, так и принятые уровни значимости, а также величины, условно называемые гипотезами.

Что такое уровень значимости?

Понятие «уровень» входит в основные критерии статистической значимости. Используется оно в прикладной и практической статистике. Это своего рода величина, учитывающая вероятность возможных отклонений или ошибок.

Уровень основывается на выявлении различий в готовых выборках, позволяет установить их существенность либо же, наоборот, случайность. У этого понятия есть не только цифровые значения, но и их своеобразные расшифровки. Они объясняют то, как нужно понимать значение, а сам уровень определяется сравнением результата с усредненным индексом, это и выявляет степень достоверности различий.

Таким образом, можно представить понятие уровня просто - это показатель допустимой, вероятной погрешности или же ошибки в сделанных из полученных статистических данных выводах.

Какие уровни значимости используются?

Статистическая значимость коэффициентов вероятности допущенной ошибки на практике отталкивается от трех базовых уровней.

Первым уровнем считается порог, при котором значение равно 5 %. То есть вероятность погрешности не превышает уровня значимости в 5 %. Это означает, что уверенность в безупречности и безошибочности выводов, сделанных на основе данных статистических исследований, составляет 95 %.

Вторым уровнем является порог в 1 %. Соответственно, эта цифра означает, что руководствоваться полученными при статистических расчетах данными можно с уверенностью в 99 %.

Третий уровень - 0,1 %. При таком значении вероятность наличия ошибки равна доле процента, то есть погрешности практически исключаются.

Что такое гипотеза в статистике?

Ошибки как понятие разделяются по двум направлениям, касающимся принятия или же отклонения нулевой гипотезы. Гипотеза - это понятие, за которым скрывается, согласно определению, набор иных данных или же утверждений. То есть описание вероятностного распределения чего-либо, относящегося к предмету статистического учета.

Гипотез при простых расчетах бывает две - нулевая и альтернативная. Разница между ними в том, что нулевая гипотеза берет за основу представление об отсутствии принципиальных отличий между участвующими в определении статистической значимости выборками, а альтернативная ей полностью противоположна. То есть альтернативная гипотеза основана на наличии весомой разницы в данных выборок.

Какими бывают ошибки?

Ошибки как понятие в статистике находятся в прямой зависимости от принятия за истинную той или иной гипотезы. Их можно разделить на два направления или же типа:

• первый тип обусловлен принятием нулевой гипотезы, оказавшейся неверной;
• второй - вызван следованием альтернативной.

Первый тип ошибок называется ложноположительным и встречается достаточно часто во всех сферах, где используются статистические данные. Соответственно, ошибка второго типа называется ложноотрицательной.

Для чего нужна регрессия в статистике?

Статистическая значимость регрессии в том, что с ее помощью можно установить, насколько соответствует реальности вычисленная на основе данных модель различных зависимостей; позволяет выявить достаточность или же нехватку факторов для учета и выводов.

Определяется регрессивное значение с помощью сравнения результатов с перечисленными в таблицах Фишера данными. Или же при помощи дисперсионного анализа. Важное значение показатели регрессии имеют при сложных статистических исследованиях и расчетах, в которых участвует большое количество переменных величин, случайных данных и вероятных изменений.

Основные черты всякой зависимости между переменными.

Можно отметить два самых простых свойства зависимости между переменными: (a) величина зависимости и (b) надежность зависимости.

- Величина . Величину зависимости легче понять и измерить, чем надежность. Например, если любой мужчина в выборке имел значение числа лейкоцитов (WCC) выше чем любая женщина, то вы можете сказать, что зависимость между двумя переменными (Пол и WCC) очень высокая. Другими словами, вы могли бы предсказать значения одной переменной по значениям другой.

- Надежность ("истинность"). Надежность взаимозависимости - менее наглядное понятие, чем величина зависимости, однако чрезвычайно важное. Надежность зависимости непосредственно связана с репрезентативностью определенной выборки, на основе которой строятся выводы. Другими словами, надежность говорит о том, насколько вероятно, что зависимость будет вновь обнаружена (иными словами, подтвердится) на данных другой выборки, извлеченной из той же самой популяции.

Следует помнить, что конечной целью почти никогда не является изучение данной конкретной выборки значений; выборка представляет интерес лишь постольку, поскольку она дает информацию обо всей популяции. Если исследование удовлетворяет некоторым специальным критериям, то надежность найденных зависимостей между переменными выборки можно количественно оценить и представить с помощью стандартной статистической меры.

Величина зависимости и надежность представляют две различные характеристики зависимостей между переменными. Тем не менее, нельзя сказать, что они совершенно независимы. Чем больше величина зависимости (связи) между переменными в выборке обычного объема, тем более она надежна (см. следующий раздел).

Статистическая значимость результата (p-уровень) представляет собой оцененную меру уверенности в его "истинности" (в смысле "репрезентативности выборки"). Выражаясь более технически, p-уровень – это показатель, находящийся в убывающей зависимости от надежности результата. Более высокий p-уровень соответствует более низкому уровню доверия к найденной в выборке зависимости между переменными. Именно, p-уровень представляет собой вероятность ошибки, связанной с распространением наблюдаемого результата на всю популяцию.

Например, p-уровень = 0.05 (т.е. 1/20) показывает, что имеется 5% вероятность, что найденная в выборке связь между переменными является лишь случайной особенностью данной выборки. Во многих исследованиях p-уровень 0.05 рассматривается как "приемлемая граница" уровня ошибки.

Не существует никакого способа избежать произвола при принятии решения о том, какой уровень значимости следует действительно считать "значимым". Выбор определенного уровня значимости, выше которого результаты отвергаются как ложные, является достаточно произвольным.

На практике окончательное решение обычно зависит от того, был ли результат предсказан априори (т.е. до проведения опыта) или обнаружен апостериорно в результате многих анализов и сравнений, выполненных с множеством данных, а также на традиции, имеющейся в данной области исследований.

Обычно во многих областях результат p .05 является приемлемой границей статистической значимости, однако следует помнить, что этот уровень все еще включает довольно большую вероятность ошибки (5%).

Результаты, значимые на уровне p .01 обычно рассматриваются как статистически значимые, а результаты с уровнем p .005 или p . 001 как высоко значимые. Однако следует понимать, что данная классификация уровней значимости достаточно произвольна и является всего лишь неформальным соглашением, принятым на основе практического опыта в той или иной области исследования .

Понятно, что чем большее число анализов будет проведено с совокупностью собранных данных, тем большее число значимых (на выбранном уровне) результатов будет обнаружено чисто случайно.

Некоторые статистические методы, включающие много сравнений, и, таким образом, имеющие значительный шанс повторить такого рода ошибки, производят специальную корректировку или поправку на общее число сравнений. Тем не менее, многие статистические методы (особенно простые методы разведочного анализа данных) не предлагают какого-либо способа решения данной проблемы.

Если связь между переменными "объективно" слабая, то не существует иного способа проверить такую зависимость кроме как исследовать выборку большого объема. Даже если выборка совершенно репрезентативна, эффект не будет статистически значимым, если выборка мала. Аналогично, если зависимость "объективно" очень сильная, тогда она может быть обнаружена с высокой степенью значимости даже на очень маленькой выборке.

Чем слабее зависимость между переменными, тем большего объема требуется выборка, чтобы значимо ее обнаружить.

Разработано много различных мер взаимосвязи между переменными. Выбор определенной меры в конкретном исследовании зависит от числа переменных, используемых шкал измерения, природы зависимостей и т.д.

Большинство этих мер, тем не менее, подчиняются общему принципу: они пытаются оценить наблюдаемую зависимость, сравнивая ее с "максимальной мыслимой зависимостью" между рассматриваемыми переменными. Говоря технически, обычный способ выполнить такие оценки заключается в том, чтобы посмотреть, как варьируются значения переменных и затем подсчитать, какую часть всей имеющейся вариации можно объяснить наличием "общей" ("совместной") вариации двух (или более) переменных.

Значимость зависит в основном от объема выборки. Как уже объяснялось, в очень больших выборках даже очень слабые зависимости между переменными будут значимыми, в то время как в малых выборках даже очень сильные зависимости не являются надежными.

Таким образом, для того чтобы определить уровень статистической значимости, нужна функция, которая представляла бы зависимость между "величиной" и "значимостью" зависимости между переменными для каждого объема выборки.

Такая функция указала бы точно "насколько вероятно получить зависимость данной величины (или больше) в выборке данного объема, в предположении, что в популяции такой зависимости нет". Другими словами, эта функция давала бы уровень значимости
(p -уровень), и, следовательно, вероятность ошибочно отклонить предположение об отсутствии данной зависимости в популяции.

Эта "альтернативная" гипотеза (состоящая в том, что нет зависимости в популяции) обычно называется нулевой гипотезой .

Было бы идеально, если бы функция, вычисляющая вероятность ошибки, была линейной и имела только различные наклоны для разных объемов выборки. К сожалению, эта функция существенно более сложная и не всегда точно одна и та же. Тем не менее, в большинстве случаев ее форма известна, и ее можно использовать для определения уровней значимости при исследовании выборок заданного размера. Большинство этих функций связано с классом распределений, называемым нормальным .

Статистическая значимость результата (p-значение) представляет собой оцененную меру уверенности в его «истинности» (в смысле «репрезентативности выборки»). Выражаясь более технически, p-значение ‑ это показатель, находящийся в убывающей зависимости от надежности результата. Более высокое p-значение соответствует более низкому уровню доверия к найденной в выборке зависимости между переменными. Именно, p-значение представляет собой вероятность ошибки, связанной с распространением наблюдаемого результата на всю популяцию. Например, p-значение=0.05 (т.е. 1/20) показывает, что имеется 5% вероятность, что найденная в выборке связь между переменными является лишь случайной особенностью данной выборки. Иными словами, если данная зависимость в популяции отсутствует, а вы многократно проводили бы подобные эксперименты, то примерно в одном из двадцати повторений эксперимента можно было бы ожидать такой же или более сильной зависимости между переменными.

Во многих исследованиях p-значение=0.05 рассматривается как «приемлемая граница» уровня ошибки.

Не существует никакого способа избежать произвола при принятии решения о том, какой уровень значимости следует действительно считать «значимым». Выбор определенного уровня значимости, выше которого результаты отвергаются как ложные, является достаточно произвольным. На практике окончательное решение обычно зависит от того, был ли результат предсказан априори (т.е. до проведения опыта) или обнаружен апостериорно в результате многих анализов и сравнений, выполненных с множеством данных, а также на традиции, имеющейся в данной области исследований. Обычно во многих областях результат p 0.05 является приемлемой границей статистической значимости, однако следует помнить, что этот уровень все еще включает довольно большую вероятность ошибки (5%). Результаты, значимые на уровне p 0.01 обычно рассматриваются как статистически значимые, а результаты с уровнем p 0.005 или p 0.001 как высоко значимые. Однако следует понимать, что данная классификация уровней значимости достаточно произвольна и является всего лишь неформальным соглашением, принятым на основе практического опыта в той или иной области исследования.

Как было уже сказано, величина зависимости и надежность представляют две различные характеристики зависимостей между переменными. Тем не менее, нельзя сказать, что они совершенно независимы. Говоря общим языком, чем больше величина зависимости (связи) между переменными в выборке обычного объема, тем более она надежна.

Если предполагать отсутствие зависимости между соответствующими переменными в популяции, то наиболее вероятно ожидать, что в исследуемой выборке связь между этими переменными также будет отсутствовать. Таким образом, чем более сильная зависимость обнаружена в выборке, тем менее вероятно, что этой зависимости нет в популяции, из которой она извлечена.

Объем выборки влияет на значимость зависимости. Если наблюдений мало, то соответственно имеется мало возможных комбинаций значений этих переменных и таким образом, вероятность случайного обнаружения комбинации значений, показывающих сильную зависимость, относительно велика.

Как вычисляется уровень статистической значимости. Предположим, вы уже вычислили меру зависимости между двумя переменными (как объяснялось выше). Следующий вопрос, стоящий перед вами: «насколько значима эта зависимость?» Например, является ли 40% объясненной дисперсии между двумя переменными достаточным, чтобы считать зависимость значимой? Ответ: «в зависимости от обстоятельств». Именно, значимость зависит в основном от объема выборки. Как уже объяснялось, в очень больших выборках даже очень слабые зависимости между переменными будут значимыми, в то время как в малых выборках даже очень сильные зависимости не являются надежными. Таким образом, для того чтобы определить уровень статистической значимости, вам нужна функция, которая представляла бы зависимость между «величиной» и «значимостью» зависимости между переменными для каждого объема выборки. Данная функция указала бы вам точно «насколько вероятно получить зависимость данной величины (или больше) в выборке данного объема, в предположении, что в популяции такой зависимости нет». Другими словами, эта функция давала бы уровень значимости (p-значение), и, следовательно, вероятность ошибочно отклонить предположение об отсутствии данной зависимости в популяции. Эта «альтернативная» гипотеза (состоящая в том, что нет зависимости в популяции) обычно называется нулевой гипотезой. Было бы идеально, если бы функция, вычисляющая вероятность ошибки, была линейной и имела только различные наклоны для разных объемов выборки. К сожалению, эта функция существенно более сложная и не всегда точно одна и та же. Тем не менее, в большинстве случаев ее форма известна, и ее можно использовать для определения уровней значимости при исследовании выборок заданного размера. Большинство этих функций связано с очень важным классом распределений, называемым нормальным.

В любой научно-практической ситуации эксперимента (обследования) исследователи могут исследовать не всех людей (генеральную совокупность, популяцию), а только определенную выборку. Например, даже если мы исследуем относительно небольшую группу людей, например страдающих определенной болезнью, то и в этом случае весьма маловероятно, что у нас имеются соответствующие ресурсы или необходимость тестировать каждого больного. Вместо этого обычно тестируют выборку из популяции, поскольку это удобнее и занимает меньше времени. В таком случае, откуда нам известно, что результаты, полученные на выборке, представляют всю группу? Или, если использовать профессиональную терминологию, можем ли мы быть уверены, что наше исследование правильно описывает всю популяцию , выборку из которой мы использовали?

Чтобы ответить на этот вопрос, необходимо определить статистическую значимость результатов тестирования. Статистическая значимость {Significant level , сокращенно Sig.), или /7-уровень значимости (p-level) - это вероятность того, что данный результат правильно представляет популяцию, выборка из которой исследовалась. Отметим, что это только вероятность - невозможно с абсолютной гарантией утверждать, что данное исследование правильно описывает всю популяцию. В лучшем случае по уровню значимости можно лишь заключить, что это весьма вероятно. Таким образом, неизбежно встает следующий вопрос: каким должен быть уровень значимости, чтобы можно было считать данный результат правильной характеристикой популяции?

Например, при каком значении вероятности вы готовы сказать, что таких шансов достаточно, чтобы рискнуть? Если шансы будут 10 из 100 или 50 из 100? А что если эта вероятность выше? Что можно сказать о таких шансах, как 90 из 100, 95 из 100 или 98 из 100? Для ситуации, связанной с риском, этот выбор довольно проблематичен, ибо зависит от личностных особенностей человека.

В психологии же традиционно считается, что 95 или более шансов из 100 означают, что вероятность правильности результатов достаточна высока для того, чтобы их можно было распространить на всю популяцию. Эта цифра установлена в процессе научно-практической деятельности - нет никакого закона, согласно которому следует выбрать в качестве ориентира именно ее (и действительно, в других науках иногда выбирают другие значения уровня значимости).

В психологии оперируют этой вероятностью несколько необычным образом. Вместо вероятности того, что выборка представляет популяцию, указывается вероятность того, что выборка не представляет популяцию. Иначе говоря, это вероятность того, что обнаруженная связь или различия носят случайный характер и не являются свойством совокупности. Таким образом, вместо того чтобы утверждать, что результаты исследования правильны с вероятностью 95 из 100, психологи говорят, что имеется 5 шансов из 100, что результаты неправильны (точно так же 40 шансов из 100 в пользу правильности результатов означают 60 шансов из 100 в пользу их неправильности). Значение вероятности иногда выражают в процентах, но чаще его записывают в виде десятичной дроби. Например, 10 шансов из 100 представляют в виде десятичной дроби 0,1; 5 из 100 записывается как 0,05; 1 из 100 - 0,01. При такой форме записи граничным значением является 0,05. Чтобы результат считался правильным, его уровень значимости должен быть ниже этого числа (вы помните, что это вероятность того, что результат неправильно описывает популяцию). Чтобы покончить с терминологией, добавим, что «вероятность неправильности результата» (которую правильнее называть уровнем значимости) обычно обозначается латинской буквой р. В описание результатов эксперимента обычно включают резюмирующий вывод, такой как «результаты оказались значимыми на уровне достоверности (р (р) менее 0,05 (т.е. меньше 5%).

Таким образом, уровень значимости (р ) указывает на вероятность того, что результаты не представляют популяцию. По традиции в психологии считается, что результаты достоверно отражают общую картину, если значение р меньше 0,05 (т.е. 5%). Тем не менее это лишь вероятностное утверждение, а вовсе не безусловная гарантия. В некоторых случаях этот вывод может оказаться неправильным. На самом деле, мы можем подсчитать, как часто это может случиться, если посмотрим на величину уровня значимости. При уровне значимости 0,05 в 5 из 100 случаев результаты, вероятно, неверны. 11а первый взгляд кажется, что это не слишком часто, однако если задуматься, то 5 шансов из 100 - это то же самое, что 1 из 20. Иначе говоря, в одном из каждых 20 случаев результат окажется неверным. Такие шансы кажутся не особенно благоприятными, и исследователи должны остерегаться совершения ошибки первого рода. Так называют ошибку, которая возникает, когда исследователи считают, что обнаружили реальные результаты, а на самом деле их нет. Противоположные ошибки, состоящие в том, что исследователи считают, будто они не обнаружили результата, а на самом деле он есть, называют ошибками второго рода.

Эти ошибки возникают потому, что нельзя исключить возможность неправильности проведенного статистического анализа. Вероятность ошибки зависит от уровня статистической значимости результатов. Мы уже отмечали, что, для того чтобы результат считался правильным, уровень значимости должен быть ниже 0,05. Разумеется, некоторые результаты имеют более низкий уровень, и нередко можно встретить результаты с такими низкими /?, как 0,001 (значение 0,001 говорит о том, что результаты могут быть неправильными с вероятностью 1 из 1000). Чем меньше значение р, тем тверже наша уверенность в правильности результатов .

В табл. 7.2 приведена традиционная интерпретация уровней значимости о возможности статистического вывода и обосновании решения о наличии связи (различий).

Таблица 7.2

Традиционная интерпретация уровней значимости, используемых в психологии

На основе опыта практических исследований рекомендуется: чтобы по возможности избежать ошибок первого и второго рода, при ответственных выводах следует принимать решения о наличии различий (связи), ориентируясь на уровень р п признака.

Статистический критерий (Statistical Test) - это инструмент определения уровня статистической значимости. Это решающее правило, обеспечивающее принятие истинной и отклонение ложной гипотезы с высокой вероятностью .

Статистические критерии обозначают также метод расчета определенного числа и само это число. Все критерии используются с одной главной целью: определить уровень значимости анализируемых с их помощью данных (т.е. вероятность того, что эти данные отражают истинный эффект, правильно представляющий популяцию, из которой сформирована выборка).

Некоторые критерии можно использовать только для нормально распределенных данных (и если признак измерен по интервальной шкале) - эти критерии обычно называют параметрическими. С помощью других критериев можно анализировать данные практически с любым законом распределения - их называют непараметрическими.

Параметрические критерии - критерии, включающие в формулу расчета параметры распределения, т.е. средние и дисперсии (^-критерий Стью- дента, F-критерий Фишера и др.).

Непараметрические критерии - критерии, не включающие в формулу расчета параметров распределения и основанные на оперировании частотами или рангами (критерий Q Розенбаума, критерий U Манна - Уитни

Например, когда мы говорим, что достоверность различий определялась по ^-критерию Стьюдента, то имеется в виду, что использовался метод ^-критерия Стьюдента для расчета эмпирического значения, которое затем сравнивается с табличным (критическим) значением.

По соотношению эмпирического (нами вычисленного) и критического значений критерия (табличного) мы можем судить о том, подтверждается или опровергается наша гипотеза. В большинстве случаев для того, чтобы мы признали различия значимыми, необходимо, чтобы эмпирическое значение критерия превышало критическое, хотя есть критерии (например, критерий Манна - Уитни или критерий знаков), в которых мы должны придерживаться противоположного правила.

В некоторых случаях расчетная формула критерия включает в себя количество наблюдений в исследуемой выборке, обозначаемое как п. По специальной таблице мы определяем, какому уровню статистической значимости различий соответствует данная эмпирическая величина. В большинстве случаев одно и то же эмпирическое значение критерия может оказаться значимым или незначимым в зависимости от количества наблюдений в исследуемой выборке (п ) или от так называемого количества степеней свободы , которое обозначается как v (г>) или как df (иногда d).

Зная п или число степеней свободы, мы по специальным таблицам (основные из них приводятся в приложении 5) можем определить критические значения критерия и сопоставить с ними полученное эмпирическое значение. Обычно это записывается так: «при п = 22 критические значения критерия составляют t St = 2,07» или «при v (d ) = 2 критические значения критерия Стьюдента составляют = 4,30» и т.н.

Обычно предпочтение оказывается все же параметрическим критериям, и мы придерживаемся этой позиции. Считается, что они более надежны, и с их помощью можно получить больше информации и провести более глубокий анализ. Что касается сложности математических вычислений, то при использовании компьютерных программ эта сложность исчезает (но появляются некоторые другие, впрочем, вполне преодолимые).

• В настоящем учебнике мы подробно не рассматриваем проблему статистических
• гипотез (нулевой - Я0 и альтернативной - Нj) и принимаемые статистические решения,поскольку студенты-психологи изучают это отдельно по дисциплине «Математическиеметоды в психологии». Кроме того, необходимо отметить, что при оформлении исследовательского отчета (курсовой или дипломной работы, публикации) статистические гипотезыи статистические решения, как правило, не приводятся. Обычно при описании результатовуказывают критерий, приводят необходимые описательные статистики (средние, сигмы,коэффициенты корреляции и т.д.), эмпирические значения критериев, степени свободыи обязательно р-уровень значимости. Затем формулируют содержательный вывод в отношении проверяемой гипотезы с указанием (обычно в виде неравенства) достигнутого илинедостигнутого уровня значимости.

Задание 3. Пяти дошкольникам предъявляют тест. Фиксируется время решения каждого задания. Будут ли найдены статистически значимые различия между временем решения первых трёх заданий теста?

Справочный материал

Данное задание основано на теории дисперсионного анализа. В общем случае, задачей дисперсионного анализа является выявление тех факторов, которые оказывают существенное влияние на результат эксперимента. Дисперсионный анализ может применяться для сравнения средних нескольких выборок, если число выборок больше двух. Для этой цели служит однофакторный дисперсионный анализ.

В целях решения поставленных задач принимается следующее. Если дисперсии полученных значений параметра оптимизации в случае влияния факторов отличаются от дисперсий результатов в случае отсутствия влияния факторов, то такой фактор признается значимым.

Как видно из формулировки задачи, здесь используются методы проверки статистических гипотез, а именно – задача проверки двух эмпирических дисперсий. Следовательно, дисперсионный анализ базируется на проверке дисперсий по критерию Фишера. В данном задании необходимо проверить являются ли статистически значимыми различия между временем решения первых трёх заданий теста каждым из шести дошкольников.

Нулевой (основной) называют выдвинутую гипотезу H о. Сущность е сводится к предположению, что разница между сравниваемыми параметрами равна нулю (отсюда и название гипотезы – нулевая) и что наблюдаемые различия имеют случайный характер.

Конкурирующей (альтернативной) называют гипотезу H 1 , которая противоречит нулевой.

Решение:

Методом дисперсионного анализа при уровне значимости α = 0,05 проверим нулевую гипотезу (H о) о существовании статистически значимых различий между временем решения первых трёх заданий теста у шести дошкольников.

Рассмотрим таблицу условия задания, в которой найдем среднее время решения каждого из трех заданий теста

Находим общую среднюю:

Для того, чтобы учесть значимость временных различий каждого теста, общая выборочная дисперсия разбивается на две части, первая из которых называется факторной , а вторая – остаточной

Рассчитаем общую сумму квадратов отклонений вариант от общей средней по формуле

или , где р – число измерений времени решений заданий теста, q – количество испытуемых. Для этого составим таблицу квадратов вариант