Vortrag zum Thema praktische Anwendungen der Ähnlichkeit von Dreiecken. Videolektion „Praktische Anwendungen der Dreiecksähnlichkeit. Präsentation für eine Unterrichtsstunde in Geometrie (Klasse 8) zum Thema: Praktische Anwendungen der Ähnlichkeit von Dreiecken

Geometrieunterricht in der 8. Klasse zum Thema "Praktische Anwendung der Ähnlichkeit von Dreiecken" für das Schuljahr 2016-2017.

"Geometrie ist das Mächtigste
ein Mittel, um unseren Geist zu verfeinern
Fähigkeiten und gibt Ihnen die Möglichkeit dazu
denken und argumentieren."
G. Galileo

Das Ziel des Unterrichts: zu lehren, wie man theoretisches Wissen zur Lösung von Problemen mit praktischem Inhalt anwendet.

Aufgaben:

Lehrreich:

verallgemeinern und systematisieren das Wissen zum Thema: „Ähnlichkeitszeichen von Dreiecken“;

Entwicklung von Fähigkeiten zur Verallgemeinerung, Abstraktion und Konkretisierung der Eigenschaften der untersuchten Objekte und Beziehungen und deren Anwendung bei der Lösung praktischer Probleme;

die Ausbildung der Fähigkeiten der Schüler bei der Anwendung der Ähnlichkeitszeichen von Dreiecken bei der Lösung von Problemen fortzusetzen.

Entwicklung:

entwickeln Sie logisches Denken, die Fähigkeit zu vergleichen, zu verallgemeinern und Schlussfolgerungen zu ziehen;

das Interesse der Schüler am Studienfach wecken;

Entwicklung der kreativen Fähigkeiten der Schüler

Entwicklung von Fähigkeiten zur Verallgemeinerung, Abstraktion und Konkretisierung der Eigenschaften der untersuchten Objekte und Beziehungen und deren Anwendung bei der Lösung praktischer Probleme

Lehrreich:

bilden die Motive kognitiver Aktivität,

ästhetische Erziehung der Schüler.

Fähigkeiten entwickeln, um Ihren Wissensstand zu dem Thema einzuschätzen;

Entwicklung einer Sprachkultur, kognitives Interesse;

Ausrüstung :

• Multimedia-Projektor, Leinwand;

  Präsentation zur Unterrichtsbegleitung ;

  Handzettel.

Unterrichtstyp: Problemlösungsworkshop

Unterrichtsstruktur:

Zeit organisieren.

Aktualisierung des Grundwissens:
a) Überprüfen der ZUN von Studenten;
b) Wiederholung von theoretischem Stoff;
in) mündliche Problemlösung.

Psychische Entlastung

Workshop zur Problemlösung: Unterhaltsame Probleme lösen.

Sportminuten (für die Augen, um Verspannungen im Schultergürtel zu lösen)

Zusätzliches Material

Hausaufgaben.

Gruppenarbeit

Zusammenfassung der Lektion. Reflexion. Selbstachtung

Gebrauchte Bücher:

Geometrie, 7-9: Lehrbuch. für Allgemeinbildung Institutionen/ [L.S. Atanasyan, V.F. Butuzov, S.B. Kadomtsev und andere] - 16. Aufl. – M.: Aufklärung; JSC "Mosk. Lehrbuch, 2006

Das Studium der Geometrie in den Klassen 7-9: Methode. Empfehlungen für Lehrbücher: Buch. für den Lehrer / L.S. Atanasyan, V.F. Butuzov, Yu.A. Glazkov und andere - M .: Bildung, 1997

UND I. Depman Die Welt der Zahlen. Geschichten über Mathematik. - L .: Kinderliteratur, 1975

Während des Unterrichts

I. Organisatorischer Moment.

II. Das Wort des Lehrers über den Zweck dieser Lektion.

Das Dreieck ist die einfachste geometrische Figur, die uns seit unserer Kindheit vertraut ist. Wir beziehen uns im Geometrieunterricht am häufigsten auf das Dreieck. Diese Figur ist voller interessanter und mysteriöser Dinge, wie das Bermuda-Dreieck, in dem Schiffe und Flugzeuge spurlos verschwinden.Ein weiser Mann sagte: „Die höchste Manifestation des Geistes ist der Verstand. Die höchste Manifestation des Geistes ist die Geometrie. Die Geometriezelle ist ein Dreieck. Es ist so unerschöpflich wie das Universum." Dies ist eines der Hauptthemen des Schulplanimetriekurses. Die Fähigkeit, Probleme für die Verwendung von Ähnlichkeitsmerkmalen zu lösen, wird in der Geometrie, Physik und Astronomie häufig verwendet.

In der heutigen Lektion werden wir uns der Lösung von Problemen zum Thema widmen:Praktische Anwendung ähnlicher Dreiecke ". Dies ist eine Workshop-Lektion, in der wir uns mit der Verwendung von Ähnlichkeitsmerkmalen bei der Lösung unterhaltsamer Probleme befassen.

Notieren Sie das Datum, die Aufgaben und das Thema der Lektion.

III. Aktualisierung des Grundwissens.

Damit der Unterricht erfolgreich ist, ist es notwendig, den theoretischen Stoff zu wiederholen. Aber lassen Sie uns zuerst überprüfen, wie Sie den Hausaufgabenstoff gelernt haben.

Daher biete ich Ihnen einen kleinen Test für 3-5 Minuten an.

a) Testen zum Thema „Ähnliche Dreiecke“

b) Wiederholung des theoretischen Materials:

Jetzt beantworte mir bitte die Fragen:

Welche Dreiecke sind ähnlich?

Welche Seiten von Dreiecken heißen ähnlich?

Was ist der Ähnlichkeitskoeffizient? (Zahl k gleich dem Verhältnis ähnlicher Seiten)

Was sind die Kriterien für die Ähnlichkeit von Dreiecken?

Wie groß ist das Flächenverhältnis zweier ähnlicher Dreiecke?

c) Mündliche Problemlösung:

- Nennen Sie ähnliche Dreiecke. Inwiefern ähneln sie sich?

Nennen Sie die Eigenschaften ähnlicher Dreiecke

IV. Psychische Entlastung

V. Unterhaltungsprobleme lösen.

Geometrie ist nicht nur die Wissenschaft von den Eigenschaften von Dreiecken, Parallelogrammen, Kreisen. Geometrie ist eine ganze Welt, die uns von Geburt an umgibt. Schließlich hat alles, was wir sehen, auf die eine oder andere Weise mit Geometrie zu tun, nichts entgeht seinem aufmerksamen Blick. Geometrie hilft einem Menschen, mit offenen Augen durch die Welt zu gehen, lehrt, sich sorgfältig umzusehen und die Schönheit gewöhnlicher Dinge zu sehen, zu schauen und zu denken, zu denken und Schlussfolgerungen zu ziehen.

Die Geometrie ist eine der ältesten Wissenschaften. Es entstand aus der praktischen Tätigkeit von Menschen und diente zu Beginn seiner Entwicklung vor allem praktischen Zwecken. In der Zukunft wurde die Geometrie als eigenständige Wissenschaft gebildet, die sich mit dem Studium geometrischer Formen befasste.

Beim Studium der Geometrie sind Sie auf ähnliche Figuren gestoßen. Heute werden wir diskutieren, wie die Eigenschaften solcher Dreiecke genutzt werden können, um verschiedene Messungen am Boden durchzuführen. Betrachten Sie die Aufgaben:

Bestimmung der Höhe eines Objekts; Bestimmen der Entfernung zu einem unzugänglichen Objekt

Und jetzt möchte ich Ihnen ein altes Problem anbieten.

Aufgabe 1 . Der griechische Weise Thales bestimmte sechs Jahrhunderte vor unserer Zeitrechnung die Höhe der Pyramide in Ägypten. Er nutzte ihren Schatten aus. Die Priester und der Pharao, die sich am Fuß der höchsten Pyramide versammelt hatten, blickten verwirrt auf den nördlichen Fremden, der die Höhe des riesigen Bauwerks erriet.
Thales, sagt die Legende, wählte den Tag und die Stunde, wenn die Länge seines eigenen Schattens seiner Körpergröße entsprach; An diesem Punkt muss die Höhe der Pyramide auch gleich der Länge des Schattens sein, den sie wirft. Natürlich musste die Länge des Schattens passen
Zählen Sie vom Mittelpunkt der quadratischen Basis der Pyramide; Thales konnte die Breite dieser Basis direkt messen.

Also lehrte Thales die Ägypter, die Höhe der Pyramide anhand der Länge ihres Schattens zu bestimmen:

Wie das gemacht wurde, geht aus dem Bild hervor.

Er maß den Schatten des Stocks und den Schatten der Pyramide. Thales verglich das Verhältnis der Höhe realer Objekte mit der Länge ihrer Schatten und fand die Höhe der Pyramide

Ändern wir diese Methode so, dass Sie an einem sonnigen Tag jeden Schatten verwenden können, egal wie lang er ist. Die Länge der Stange sei 1 m und ihr Schatten 1,2 m. Finden Sie die Höhe des Baumes, wennsein Schatten ist 6m.

AB ist die Länge des Stocks,DEist die Höhe der Pyramide.

 ABC ist wie BEIDE(an zwei Ecken):

 SVA= BEIEd=90°;

 DIA = DBE, weil entsprechend AC ||DB und Sekante SW (Sonnenstrahlen fallen parallel)

;
.

So fand Thales die Höhe der Pyramide.

Die von Thales vorgeschlagene Methode ist jedoch nicht immer anwendbar. Warum?

Bestimmung der Höhe eines Objekts.

Es gibt mehrere einfache Möglichkeiten, die Höhe von Objekten zu bestimmen. Solche Methoden sind zum Beispiel im Handbuch eines Jäger-Sportlers angegeben.

Folie 6

Durch Schatten . An einem sonnigen Tag ist es nicht schwierig, die Höhe eines Objekts, beispielsweise eines Baums, anhand seines Schattens zu messen. Sie müssen sich nur von der folgenden Regel leiten lassen: Die Höhe des gemessenen Baums ist so oft die Höhe eines Ihnen bekannten Objekts (z. B. eines Stocks oder einer Waffe), wie oft der Schatten des Baums ist größer als der Schatten des Stocks. Wenn nach unserer Messung der Schatten einer Waffe oder eines Stocks doppelt so lang ist wie die Waffe oder der Stock, dann ist die Höhe des Baums halb so lang wie sein Schatten. Im gleichen Fall, wenn der Schatten einer Waffe oder eines Stocks gleich ihrer Länge ist, ist die Höhe des Baums auch gleich seinem Schatten.

Aufgabe 2. Sherlock Holmes

Pole . Diese Methode kann verwendet werden, wenn keine Sonne scheint und kein Schatten von Objekten sichtbar ist. Zum Messen müssen Sie eine Stange nehmen, die Ihrer Körpergröße entspricht. Dieser Mast muss in einem solchen Abstand vom Baum montiert werden, dass man im Liegen die Baumkrone in einer geraden Linie mit der obersten Spitze des Mastes sehen kann. Dann entspricht die Höhe des Baumes der Linie, die von Ihrem Kopf bis zum Fuß des Baumes gezogen wird.

Aufgabe 3. Das Folgende ist auch eine sehr einfache Art, hohe Objekte zu messen, die von Jules Verne in dem berühmten Roman bildhaft beschrieben wurde"Mysteriöse Insel" . Hat jemand diesen Roman gelesen?

…Der Ingenieur nahm eine gerade Stange mit einer Länge von 12 Fuß (1 Fuß \u003d 30 cm), maß sie so genau wie möglich und verglich sie mit seiner Größe, die ihm bekannt war. Der Ingenieur erreichte keine 500 Fuß von der Granitwand, die steil aufragte, steckte eine Stange etwa zwei Fuß in den Sand und stellte sie, nachdem er sie fest verstärkt hatte, mit einem Lot senkrecht auf.
Dann entfernte er sich so weit vom Pfahl, dass man auf dem Sand liegend sowohl das Ende des Pfahls als auch den Rand des Grats auf derselben Linie sehen konnte. Er markierte diesen Punkt sorgfältig mit einem Stift.

– Kennst du die Grundlagen der Geometrie? fragte er Herbert und erhob sich vom Boden.
-Ja
Erinnern Sie sich an die Eigenschaften ähnlicher Dreiecke?
– Ihre ähnlichen Seiten sind proportional.
- Richtig. Also: jetzt baue ich zwei ähnliche rechtwinklige Dreiecke. Der kleinere hat eine vertikale Stange mit einem Bein, der Abstand vom Stift zur Basis der Stange ist der andere; Die Hypotenuse ist meine Sichtlinie. In einem anderen Dreieck sind die Beine: eine steile Wand, deren Höhe wir bestimmen wollen, und der Abstand vom Pflock zum Fuß dieser Wand; die Hypotenuse ist meine Sichtlinie, die mit der Richtung der Hypotenuse des ersten Dreiecks zusammenfällt …“

Die Länge der Stange beträgt also 10 Fuß (Fuß = 30 cm). Abstand vom Pflock zum Pfosten 15 Fuß, von der Wand zum Pfosten 500 Fuß. Finden Sie die Höhe der Klippe

Interessante Aufgaben? Es gibt viele so schöne Probleme, die mit Ähnlichkeitszeichen gelöst werden.

Lösung von Problem Nr. 579,

Bestimmung der Höhe eines Objekts in einer Pfütze . Diese Methode kann erfolgreich nach Regen angewendet werden, wenn viele Pfützen auf dem Boden erscheinen. Die Messung wird auf diese Weise durchgeführt: Sie finden eine Pfütze in der Nähe des gemessenen Objekts und stellen sich in die Nähe, sodass sie zwischen Ihnen und dem Objekt platziert wird. Danach wird ein Punkt gefunden, von dem aus die Oberseite des im Wasser gespiegelten Objekts sichtbar ist. Das gemessene Objekt, zum Beispiel ein Baum, wird so oft höher sein als Sie, wie viel die Entfernung von ihm zur Pfütze größer ist als die Entfernung von der Pfütze zu Ihnen.

Anstelle einer Pfütze können Sie einen horizontal platzierten Spiegel verwenden. Essen. Der Spiegel ist gelegthorizontal und bewegen Sie sich von ihm weg zurück zu einem Punkt, an dem der Betrachter, an dem stehend, die Spitze des Baums im Spiegel sieht. Ein LichtstrahlFD, reflektiert vom Spiegel an der StelleDdringt in das menschliche Auge ein.

 ABDähnlich EFD(an zwei Ecken):

 VAD=  GEFÜTTERT=90°;

 UNDDB = EDF, da der Einfallswinkel ist gleich dem Reflexionswinkel.

In ähnlichen Dreiecken sind ähnliche Seiten proportional:

;
.

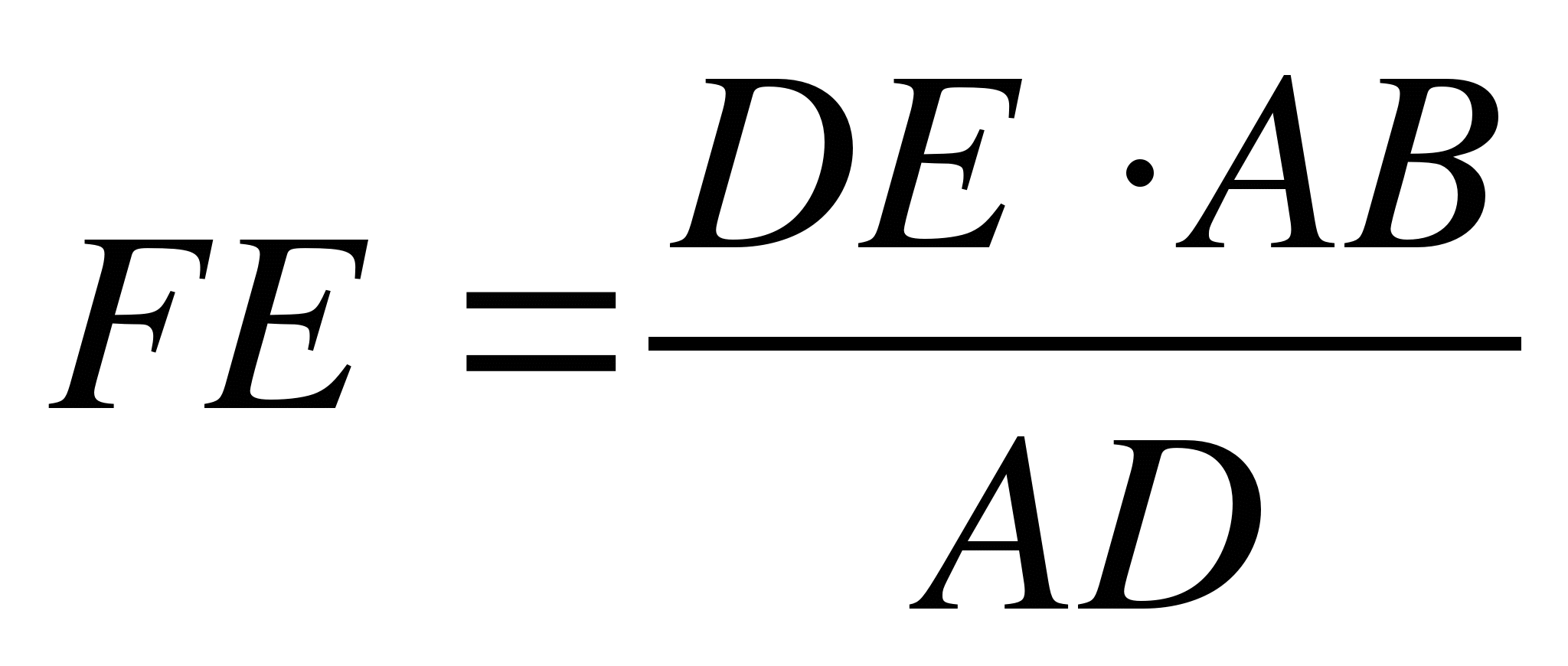Somit wird die Höhe des Objekts gefunden.

Bestimmung der Höhe eines Objekts mit einem Spiegel . №581

Arbeitet auf dem Boden

Zusätzliches Material. 7.1. Zum „Durchführen“ langer Segmente am Boden wird eine Technik genanntgerade hängen. Dieser Ansatz ist wie folgt:

Zunächst werden einige Punkte A und B markiert, dazu werden zwei Meilensteine ​​verwendet – etwa 2 m lange Stangen, die an einem Ende zugespitzt sind, damit sie in den Boden gesteckt werden können. Der dritte Meilenstein (Punkt C) wird so gesetzt, dass die Meilensteine ​​an den Punkten A und B ihn vom Beobachter aus, der sich an Punkt A befindet, überdecken. Der nächste Meilenstein wird so gesetzt, dass er von den Meilensteinen an den Punkten B und C überdeckt wird usw.

7.2. Die Winkelmessung am Boden erfolgt mit speziellen Instrumenten. Die einfachste von ihnen istAstrolabium. Das Astrolabium besteht aus zwei Teilen: einer in Grade unterteilten Scheibe und einem Lineal (Alidade), das sich um die Mitte der Scheibe dreht. An den Enden der Allidade befinden sich zwei schmale Fenster, die dazu dienen, sie in eine bestimmte Richtung zu lenken.

Um zu messen AOB auf dem Boden, ein Stativ mit einem Astrolabium wird so aufgestellt, dass das Lot, das von der Mitte der Scheibe hängt, genau über dem Punkt O liegt. Dann wird die Allidade entlang einer der Seiten des OA oder OB installiert, und die Teilung ist markiert, an der sich der Alidadenzeiger befindet. Als nächstes drehen Sie die Alhidade, indem Sie sie entlang der anderen Seite des gemessenen Winkels führen, und markieren Sie die Teilung, an der der Alidade-Zeiger anliegen wird. Der Unterschied in Referenz und gibt ein Gradmaß an AOW.

Die Winkelmessung am Boden erfolgt mit speziellen Instrumenten.

Holzfäller Regel

Bestimmung der Entfernung zu einem unzugänglichen Punkt

Zuerst müssen Sie sich merken, wie lange gerade Segmente auf dem Boden gezeichnet und Winkel gemessen werden.

gerade hängen .

Astrolabium .

Folie 11

 A und C. Sie bauen auf einem Stück Papier auf UND 1 BEI 1 VON 1 , welcher A= UND 1 und C= VON 1 1 BEI 1 und ein 1 VON 1 .

Durch den Bau ABC ist wie UND 1 BEI 1 VON 1 (zwei Ecken).

1) Zum "Durchführen" langer Segmente am Boden, eine Technik genanntgerade hängen .

Die Messung von Winkeln am Boden kann mit einem speziellen Gerät durchgeführt werden -Astrolabium .

Folie 11

Angenommen, Sie müssen die Entfernung von Punkt A zu einem unzugänglichen Objekt B finden. Dazu wird Punkt C am Boden ausgewählt, das Segment AC aufgehängt und gemessen. Messen Sie dann mit einem Astrolabium A und C. Sie bauen auf einem Stück Papier auf UND 1 BEI 1 VON 1 , welcher A= UND 1 und C= VON 1 . Als nächstes messen Sie die Längen der Seiten A 1 ;
.

Somit wird die Entfernung zu einem unzugänglichen Punkt gefunden

Lösungsaufgaben Nr. 582,

№583 . Praktische Aufgabe.

Es wird vorgeschlagen, Problem Nr. 583 in Paararbeit zu lösen.

Es schlägt vor, anhand der Ähnlichkeit von Dreiecken die Breite des Flusses zu messen.

Die Zeichnung für das Problem ist im Lehrbuch verfügbar. Sie müssen erklären, wie eine solche Zeichnung erhalten wurde, die Ähnlichkeit von Dreiecken beweisen und Berechnungen durchführen.

Folie 12

V. Selbständiges Arbeiten in Gruppen

Aufgaben 1,2,3,4 Folie(33-36)

VI. Hausaufgaben:

S. 64, Nr. 580.582

VI. Unterrichtsergebnisse. Schätzungen.

– Was hast du heute Neues gelernt?

Heute haben Sie in der Lektion mit der einfachsten geometrischen Figur gearbeitet, die als „Geometriezelle“ bezeichnet wird. Beim Lösen verschiedener Probleme bei der Verwendung von Zeichen der Ähnlichkeit von Dreiecken haben Sie gelernt, logisch richtig zu denken, zu vergleichen, zu verallgemeinern, Schlussfolgerungen zu ziehen und dabei Ihr Denken zu entwickeln Fähigkeiten.

Um die Vorschau von Präsentationen zu verwenden, erstellen Sie ein Google-Konto (Konto) und melden Sie sich an: https://accounts.google.com

Beschriftungen der Folien:

Praktische Anwendungen ähnlicher Dreiecke

Überprüfung der Testaufgabe Nr. Option Nr. 1 Option Nr. 2 Nr. 1 1 2 Nr. 2 3 4 Nr. 3 3 2 Nr. 4 1 4 Nr. 5 2 1

„5“ – 5 Aufgaben „4“ – 4 Aufgaben „3“ – 3 Aufgaben „2“ – weniger als 3 Aufgaben

Die Bewohner des alten Ägypten stellten sich die Frage: "Wie findet man die Höhe einer der riesigen Pyramiden?" Thales hat eine Lösung für dieses Problem gefunden. Er steckte einen langen Stock senkrecht in den Boden und sagte: "Wenn der Schatten dieses Stocks genauso lang ist wie der Stock selbst, wird der Schatten der Pyramide genauso lang sein wie die Höhe der Pyramide."

Ähnlichkeitseigenschaften werden in der Praxis seit langem häufig beim Erstellen von Plänen, Karten, beim Erstellen von Architekturzeichnungen und Zeichnungen verschiedener Teile von Maschinen und Mechanismen verwendet.

Ermitteln Sie die Höhe eines Gebäudes (in Metern), dessen Sonnenschatten 27 m beträgt, und der Sonnenschatten einer 1 m 60 cm großen Person 2 m 40 cm beträgt.

Finden Sie die Breite des Flusses (CB), wenn Sie durch einige Messungen auf einer Seite des Flusses (AB=5 m, AD=12 m, AM=3 m) zwei ähnliche Dreiecke ACD und ABM konstruieren können.

Ein 8,8 m hoher Baum wirft Schatten. Es verdunkelt einen 4 m hohen Baum, der sich in einem Abstand von 6 m von ihm befindet, vollständig vor der Sonne, wie in der Abbildung gezeigt. Bestimmen Sie, wie weit der größere Baum seinen Schatten wirft. Geben Sie Ihre Antwort in Metern an.

H - 20 E - 18 R - 15 V - 11 11 18 15 20

11 18 15 20 V E R N

In der Art von Jules Verne (1828-1905)

Die Welt um uns herum ist eine Welt der Geometrie, rein, wahr, makellos in unseren Augen. Rundum alles – die Geometrie von Le Corbusier

BEWERTEN SIE IHRE ARBEIT IN DER LEKTION "+" - hat die Aufgabe bewältigt "+ -" - es gab Schwierigkeiten "-" - hat die Aufgabe nicht bewältigt

Ein Lichtstrahl, der von einer Lichtquelle auf einem 12 m hohen vertikalen Mast ausgeht und von einer horizontalen Spiegelfläche reflektiert wird, trifft auf einen Empfänger, der sich auf einem anderen 6 m hohen vertikalen Mast befindet. Der Einfallswinkel eines Lichtstrahls ist gleich dem Reflexionswinkel, wie in der Abbildung gezeigt. Der Abstand zwischen den Mastfüßen beträgt 15 m. Ermitteln Sie den Abstand zwischen dem Mastfuß der Lichtquelle und dem Reflexionspunkt.

Die Leiter verbindet die Punkte A und B. Die Höhe jeder Stufe beträgt 24 cm und die Länge 70 cm. Der Abstand zwischen den Punkten A und B beträgt 29,6 m. Finde die Höhe, bis zu der die Leiter ansteigt (in Metern).

Zum Thema: Methodische Entwicklungen, Präsentationen und Notizen

Dieses Material bietet einen detaillierten Überblick über eine Lektion in Geometrie in der 8. Klasse zum Thema "Ähnlichkeit von Dreiecken. Praktische Probleme lösen". Die Lektion wurde unter Berücksichtigung der GEF zusammengestellt ....

Wiederholung von Theoriematerial Was können die beiden oberen Dreiecke im Diagramm bedeuten? Was bedeuten die von diesen Dreiecken gezeichneten Pfeile? Formulieren Sie eine Definition von Ähnlichkeit und drei Ähnlichkeitszeichen Was sagen Ihnen die drei unteren Dreiecke? Was sind die Markierungen auf ihnen?

Prüfen. Wenn die Aussage wahr ist, antworten Sie mit "Ja", wenn sie falsch ist, nein 1. Zwei Dreiecke sind ähnlich, wenn ihre Winkel jeweils gleich sind und ähnliche Seiten proportional sind. 2. Zwei gleichseitige Dreiecke sind immer ähnlich. 3. Wenn die drei Seiten eines Dreiecks jeweils proportional zu den drei Seiten eines anderen Dreiecks sind, dann sind solche Dreiecke ähnlich. 4. Die Seiten des einen Dreiecks sind 3, 4, 6 cm lang, die Seiten des anderen Dreiecks sind 9, 14, 18 cm lang Sind diese Dreiecke ähnlich? 5. Die Umfänge ähnlicher Dreiecke stehen in Beziehung zu Quadraten mit ähnlichen Seiten. 6. Wenn zwei Winkel eines Dreiecks gleich 60 und 50 sind und zwei Winkel eines anderen Dreiecks gleich 50 und 80 sind, dann sind solche Dreiecke ähnlich. 7. Zwei rechtwinklige Dreiecke sind ähnlich, wenn sie einen gleichen spitzen Winkel haben. 8. Zwei gleichschenklige Dreiecke sind ähnlich, wenn ihre Seiten proportional sind. 9. Wenn die Segmente der Hypotenuse, in die sie durch die vom Scheitelpunkt des rechten Winkels gezogene Höhe geteilt wird, 2 und 8 cm betragen, beträgt diese Höhe 4 cm 10. Wenn die Mitte des Dreiecks 9 cm beträgt, dann der Abstand vom Scheitelpunkt des Dreiecks zum Schnittpunkt der Seitenhalbierenden beträgt 6 cm

2.

Der Satz über die Mittellinie.

Papas Stiefel und deine;….

(fortsetzen).

Im wirklichen Leben sprechen wir von ähnlichen Objekten, aber in der Geometrie sprechen wir von ähnlichen. Unsere Theorie kann also auf diese Objekte angewendet werden. Schauen wir uns die Theorie der Ähnlichkeit von Dreiecken in der Welt um uns herum an.

Lassen Sie uns das Thema der Lektion formulieren.

Partnerarbeit:

Zu

UND Stimmt es: ?ABC ∞ ?A1B1C1 wenn ∠A = 46° ∠B = 64° ∠A1 = 46° ∠C1 = 70°

L Stimmt es: ?ABC ∞ ?A1B1C1, wenn AB=13m A1B1=58m P?ABC=25m, dann P?A1B1C1=100m

b Stimmt es: ?ABC ∞ ?A1B1C1, wenn AB=15m A1B1=45m S?A1B1C1 =27m2, dann S?ABC=100m2

Zu

L

F

UND Stimmt es, wenn

Check: Welches Wort hast du bekommen? -Alpha.

* Kleine Referenz:

• In unserem Sonnensystem ist 1 Stern die Sonne.
• Sterne - im Sternbild wird der hellste Stern im Sternbild „Alpha“ genannt.
• Sterne sind für uns unzugängliche Objekte, aber sie werden studiert, sie finden die Entfernung zu ihnen.

Aber wie geht das?

Bestimmung der Entfernung zu einem unzugänglichen Punkt. Angenommen, wir müssen die Entfernung von Punkt A zu unzugänglichem Punkt B finden. Wählen Sie dazu Punkt C auf dem Boden, hängen Sie Segment AC auf und messen Sie es. Dann messen wir mit einem Astrolabium die Winkel ∠A und ∠C. Auf einem Blatt Papier bauen wir eine Art Dreieck A1B1C1, in dem ∠A1=∠A, ∠C1=∠C, und messen die Seitenlängen A1B1 und A1C1 dieses Dreiecks.

Da ?ABC ∞ ?A1B1C1 , dann = , woher. Aus den bekannten Distanzen AC, A1C1 und A1B1 finden wir die Distanz AB.

Um die Berechnungen zu vereinfachen, ist es zweckmäßig, ein Dreieck A1B1C1 zu konstruieren, so dass A1C1: AC = 1:1000. Wenn zum Beispiel AC = 130 m ist, dann nehmen Sie den Abstand A1C1 gleich 130 mm. In diesem Fall = 1000 , also wenn wir den Abstand A1B1 in Millimeter messen, erhalten wir sofort den Abstand AB in Metern.

Beispiel. Sei AC = 130m, ∠A = 73° und ∠C = 58°. Wir bauen ein Dreieck auf Papier A1B1C1 so, dass ∠A1 \u003d 73 ° und ∠С1 \u003d 58 °, A1C1 \u003d 130 mm, und messen das Segment A1B1. Sie entspricht 153 mm, also beträgt die gewünschte Entfernung 153 m.

4.

Der Priester fuhr arrogant fort:

CAB ∞ ?BDE (an 2 Ecken)

• C = ∠B (durch Bedingung)
• B = ∠E = 90°

Antwort: 146 m.

AB=2,1m AE=6,3m CB=1,7m

1. Dreiecke sind in 2 Winkeln ähnlich.

ABC ∞ ?AED (an 2 Ecken)

• Ein gemeinsames
• B = ∠E = 90°

Antwort: 5,1 m.

Pa-Beispiel:

Oh! Müde

Kaum mit dem Lehrer mithalten

Dokumentinhalt anzeigen
"Zusammenfassung einer Geometriestunde zum Thema "Praktische Anwendungen der Ähnlichkeit von Dreiecken." »

Städtische Bildungseinrichtung

"Marinekadettenschule. Admiral Kotov P. G. "

Geometriestunde (8 Zellen)

Thema: "Praktische Anwendungen der Ähnlichkeit von Dreiecken."

Skirmant Natalja Rudolfowna

Lehrer für höhere Mathematik

Geschäftsadresse:

164520, Gebiet Archangelsk,

Sewerodwinsk, st. Komsomolskaja, gest. 7,

Bürotelefon 55-20-86

Sewerodwinsk

Ziele und Ziele des Unterrichts:

die Anwendung der Dreiecksähnlichkeit bei Messarbeiten am Boden zeigen;

das Verhältnis von Theorie und Praxis aufzeigen;

den Schülern verschiedene Methoden zur Bestimmung der Höhe eines Objekts und der Entfernung zu einem unzugänglichen Objekt vorzustellen;

die Fähigkeit zu bilden, das erworbene Wissen bei der Lösung verschiedener Probleme dieser Art anzuwenden.

Lehrreich

das Interesse der Schüler am Studium der Geometrie steigern;

um die kognitive Aktivität der Schüler zu aktivieren;

die für mathematisches Handeln charakteristischen und für ein produktives Leben in der Gesellschaft notwendigen Denkqualitäten zu formen.

Lehrreich

das Interesse der Studierenden für das Fach zu wecken, indem sie in die Lösung praktischer Probleme einbezogen werden.

Während des Unterrichts:

1. Überprüfung der Hausaufgaben.

2. Test "Ist es wahr ..." (Arbeit in Paaren) - Wiederholung der Theorie.

3. Aufgabe Nr. 1. Bestimmung der Entfernung zu einem unzugänglichen Punkt (Zusammenfassung in Heften zusammen mit dem Lehrer).

4. Aufgabennummer 2. Bestimmung der Höhe eines Objekts:

a). entlang seines Schattens (entsprechend der fertigen Lösung im Lehrbuch zerlegen, Variante 1 in Heften selbst anfertigen).

b). an einer Stange (nach einer vorgefertigten Lösung in einem Lehrbuch zerlegen, Variante 2 in Heften selbst erstellen).

in). mit einem Spiegel (schlagen Sie vor, Problem Nr. 581 zu analysieren).

5. Die Ergebnisse des Unterrichts, Hausaufgabe Nr. 581.583.

1. Überprüfung der Hausaufgaben. Erläuterung der Fertiglösung Nr. 550 (1).

Gegeben: Zeichnung.

Dreiecke sind in 2 Winkeln ähnlich.

∆BAD ∞ ∆KCB (an 2 Ecken)

∠B = ∠K (durch Bedingung)

∠A = ∠C = 90°

2. Lehrer: "Leute, wir haben die ganze Theorie der Ähnlichkeit von Dreiecken studiert."

Betrachtet die Verwendung von Ähnlichkeit beim Beweis von Theoremen.

Welche Theoreme haben wir bewiesen?

Der Satz über die Mittellinie.

Eigenschaft der Seitenhalbierenden eines Dreiecks.

Im Alltag sind wir von Gegenständen gleicher Form umgeben.

Beispiel: - Tennis und Fußball;

Papas Stiefel und deine;….

(fortsetzen).

Im wirklichen Leben sprechen wir über ähnliche Dinge, aber in der Geometrie sprechen wir über ähnliche Dinge. Unsere Theorie kann also auf diese Objekte angewendet werden. Schauen wir uns die Theorie der Ähnlichkeit von Dreiecken in der Welt um uns herum an.

Lassen Sie uns das Thema der Lektion formulieren.

Schüler: "Praktische Anwendungen der Ähnlichkeit von Dreiecken."

Lehrer: „Um die Theorie anzuwenden, müssen wir sie gut kennen. Wiederholen wir:

Partnerarbeit:

Ist diese Aussage richtig. Wenn wahr, lasse den Buchstaben vor der Aussage stehen, andernfalls streiche.

Test "Ist es wahr ..." (Arbeit in Paaren) - Wiederholung der Theorie.

Zu Stimmt es, dass ähnliche Dreiecke gleiche Seiten haben?

UND Stimmt es: ∆ABC ∞ ∆A 1 B 1 C 1 wenn ∠A = 46° ∠B = 64° ∠A1 = 46° ∠C1 = 70°

L Ist es wahr, dass: ∆ABC ∞ ∆A 1 B 1 C 1 , wenn AB=13m A1B1=58m P ∆ ABC =25m, dann P ∆ A 1 B 1 C 1 =100m

b Stimmt es: ∆ABC ∞ ∆A1B1C1, wenn AB=15m A1B1=45m S ∆ A 1 B 1 C 1 =27 m 2, dann ist S ∆ ABC =100m 2

Zu Stimmt es, dass in ähnlichen Dreiecken die entsprechenden Winkel proportional sind?

L Stimmt es, (kurze Formulierung des Ähnlichkeitszeichens von Dreiecken) „Dreiecke sind in drei Winkeln ähnlich“

F Stimmt es, (kurze Formulierung des Ähnlichkeitszeichens von Dreiecken) „Dreiecke sind in zwei proportionalen Seiten und dem Winkel zwischen ihnen ähnlich“

UND Stimmt es, wenn

Check: Welches Wort hast du bekommen? -Alpha.

* Kleine Referenz:

• In unserem Sonnensystem ist 1 Stern die Sonne.

  Alle anderen Sterne befinden sich außerhalb unseres Sonnensystems.

  Die Sterne stehen im Sternbild, der hellste Stern im Sternbild heißt „Alpha“.

  Sterne sind für uns unzugängliche Objekte, aber sie werden studiert, sie finden die Entfernung zu ihnen.

Aber wie geht das?

3. Aufgabe Nr. 1. Bestimmung der Entfernung zu einem unzugänglichen Punkt (Zusammenfassung in Heften zusammen mit dem Lehrer).

Bestimmung der Entfernung zu einem unzugänglichen Punkt. Angenommen, wir müssen die Entfernung von Punkt A zu unzugänglichem Punkt B finden. Wählen Sie dazu Punkt C auf dem Boden, hängen Sie Segment AC auf und messen Sie es. Dann messen wir mit einem Astrolabium die Winkel ∠A und ∠C. Auf einem Blatt Papier bauen wir ein Dreieck ∆A 1 B 1 C 1, in dem ∠A 1 \u003d ∠A, ∠C 1 \u003d ∠C, und messen die Längen der Seiten A 1 B 1 und A 1 C 1 dieses Dreiecks.

Da ∆ABC ∞ ∆A 1 B 1 C 1 , dann = , woher. Aus den bekannten Distanzen AC, A 1 C 1 und A 1 B 1 finden wir die Distanz AB.

Zur Vereinfachung der Berechnungen ist es zweckmäßig, ein Dreieck ∆A 1 B 1 C 1 zu konstruieren, so dass A 1 C 1: AC = 1:1000. Wenn zum Beispiel AC = 130 m ist, dann wird der Abstand A 1 C 1 gleich 130 mm genommen. In diesem Fall = 1000 , also wenn wir den Abstand A 1 B 1 in Millimeter messen, erhalten wir sofort den Abstand AB in Metern.

Beispiel. Sei AC = 130m, ∠A = 73° und ∠C = 58°. Auf Papier bauen wir ein Dreieck ∆A 1 B 1 C 1 so, dass ∠A 1 \u003d 73 ° und ∠С 1 \u003d 58 °, A 1 C 1 \u003d 130 mm, und messen das Segment A 1 B 1. Sie entspricht 153 mm, also beträgt die gewünschte Entfernung 153 m.

4. Lehrer: Kommen wir zurück zu den irdischen Angelegenheiten. Griechische Wissenschaftler lösten viele praktische Probleme, die sie zuvor nicht lösen konnten. Zum Beispiel lehrte der griechische Weise Thales von Milet sechs Jahrhunderte vor unserer Zeitrechnung die Ägypter, die Höhe einer Pyramide anhand der Länge ihres Schattens zu bestimmen.

Wie es dazu kam, ist in dem Buch von Ya.I. Perelman „Unterhaltsame Geometrie“. Thales, sagt die Legende, wählte den Tag und die Stunde, wenn die Länge seines eigenen Schattens seiner Körpergröße entsprach; An diesem Punkt muss die Höhe der Pyramide auch gleich der Länge des Schattens sein, den sie wirft. Dies ist vielleicht der einzige Fall, in dem eine Person von ihrem Schatten profitiert hat. Hören wir uns ein Gleichnis an. (sagt einer der Studenten).

"Ein müder Fremder aus dem Norden kam in das Land der Großen Hapi. Die Sonne ging bereits unter, als er sich dem prächtigen Palast des Pharaos näherte und etwas zu den Dienern sagte. und vor ihm sitzt ein Pharao auf einem vergoldeten Thron, daneben ihm sind arrogante Priester, Wächter der ewigen Geheimnisse der Natur.

Wer bist du? fragte der Hohepriester.

Mein Name ist Thales. Ich komme aus Milet.

Der Priester fuhr arrogant fort:

Sie waren es also, die damit prahlten, die Höhe der Pyramide messen zu können, ohne sie zu besteigen? Die Priester krümmten sich vor Lachen.

Es wird gut sein, - fuhr der Priester spöttisch fort, - wenn du nicht mehr als hundert Ellen falsch liegst.

Ich kann die Höhe der Pyramide messen und mich um nicht mehr als eine halbe Elle irren. Ich werde es morgen machen.

Die Gesichter der Priester verfinsterten sich. Was für eine Frechheit! Dieser Fremde behauptet, in der Lage zu sein, herauszufinden, was sie, die Priester des großen Ägyptens, nicht können.

Okay, sagte der Pharao. - Es gibt eine Pyramide in der Nähe des Palastes, wir kennen ihre Höhe. Wir werden Ihre Kunst morgen überprüfen."

Am nächsten Tag fand Thales einen langen Stock und steckte ihn etwas weiter von der Pyramide entfernt in den Boden. Warten auf einen bestimmten Moment. Er maß den Schatten des Stocks und den Schatten der Pyramide. Thales verglich das Verhältnis der Höhe realer Objekte mit der Länge ihrer Schatten und fand die Höhe der Pyramide.

Aufgabennummer 2. Bestimmung der Höhe eines Objekts:

a). entlang seines Schattens (entsprechend der fertigen Lösung im Lehrbuch zerlegen, Variante 1 in Heften selbst anfertigen).

CB=8,4m BE=1022m AB=1,2m ∠C = ∠B

Dreiecke sind in 2 Winkeln ähnlich.

∆CAB ∞ ∆BDE (an 2 Ecken)

∠C = ∠B (durch Bedingung)

∠B = ∠E = 90°

Antwort: 146 m.

b). an einer Stange (nach einer vorgefertigten Lösung in einem Lehrbuch zerlegen, Variante 2 in Heften selbst erstellen).

AB=2,1m AE=6,3m CB=1,7m

Dreiecke sind in 2 Winkeln ähnlich.

∆ABC ∞ ∆AED (2 Ecken)

∠A - häufig

∠B = ∠E = 90°

Antwort: 5,1 m.

in). mit Hilfe eines Spiegels (Angebot zur Analyse von Problem Nr. 581 (D/z)).

Um die Höhe eines Baumes zu bestimmen, können Sie einen Spiegel verwenden, wie in der Abbildung gezeigt. Ein Lichtstrahl FD, der von einem Spiegel am Punkt D reflektiert wird, tritt in das menschliche Auge ein (Punkt B). Bestimmen Sie die Höhe des Baumes, wenn AC=165 cm, BC=12 cm, AD=120 cm, DE=4,8 m, ∠1 = ∠2.

5. Lehrer: Fassen wir die Lektion zusammen:

Heute haben wir in der Lektion verschiedene Möglichkeiten kennengelernt, die Höhe eines Objekts zu messen; Entfernung zu einem unzugänglichen Punkt; wendete die Ähnlichkeitstheorie an.

Formulieren Sie einen Satz, eine Phrase, Ihre Einstellung zum Unterricht und beginnen Sie mit einem Buchstaben, der im Wort "Ähnlichkeit" enthalten ist.

Pa-Beispiel:

Oh! Müde

Kaum mit dem Lehrer mithalten