Презентация 10 соотношение между синусом косинусом. Основные тригонометрические тождества, их формулировки и вывод. Закрепление изученного материала

Открытый урок по алгебре и началам анализа по теме: «Зависимость между синусом и косинусом одного и того же угла» (10 класс)

Цель: восприятие учащимися и первичное осознание нового учебного материала, осмысливание связей и отношений в объектах изучения

Образовательная : вывод формул зависимости между синусом и косинусом одного и того же угла (числа); обучение применению этих формул для вычисления значений синуса, косинуса по заданному значению одного из них.

Развивающая : учить анализировать, сравнивать, строить аналогии, обобщать и систематизировать, доказывать и опровергать, определять и объяснять понятия, развивать и совершенствовать умения применять имеющиеся у учащихся знания в различных ситуациях; развивать грамотную математическую речь учащихся, умение давать лаконичные формулировки

Воспитательная: воспитание добросовестного отношения к труду и положительного отношения к знаниям, воспитывать у учащихся аккуратность, умение слушать, высказывать свое мнение; культуру поведения.

Здоровье-сберегающая : создание комфортного психологического климата на уроке, атмосферы сотрудничества: ученик – учитель.

Знания и умения: определений основных тригонометрических функций (синуса, косинуса); знаков тригонометрических функций по четвертям; множества значений тригонометрических функций; основных формул тригонометрии. У мение правильно выбрать нужную формулу для решения конкретного задания; работать с простыми дробями; выполнять преобразование тригонометрических выражений.

Ход урока

Организационный момент:

Проверить готовность учащихся к уроку. Открытие на компьютерах сайта учителя(Приложение 1).

Устная работа по пройденной теме : «Знаки синуса, косинуса и тангенса»

На доске:

Задание:

Расставить номера четвертей координатной плоскости и определить знаки синуса, косинуса, тангенса и котангенса.

Самостоятельная работа по теме: «Знаки синуса, косинуса и тангенса»

Учащиеся открывают на сайте раздел «Задания к уроку по тригонометрии». Самопроверка

(Учащиеся выполняют задание №1, проверяют свои работы и оцениваю себя)

Объяснение нового материала

На доске:

х = … α , … ≤ cos α≤ … 2)* tg α = , α≠ …

y = … α, … ≤ sin α≤ … ctg α = , α≠ …

Задание: дописать формулы

Учитель : «Мы с вами изучили каждое понятие отдельно. Как вы считаете какую тему далее логично изучить?»

( Предполагаемый ответ: «Зависимость между этими понятиями»)

Формулируется тема урока: «Зависимость между синусом и косинусом одного и того же угла»

Учитель : «Есть несколько путей решения этой проблемы»

Используя уравнение единичной окружности

Используя теорему Пифагора

Учитель : «Давайте рассмотрим оба и выберем наиболее рациональный»

На доске:

Учащиеся выводят равенство cos 2 α + sin 2 α = 1

Учитель : «Мы получили равенство справедливое при любых значениях, входящих в него букв. Как называют такие равенства?»

( Предполагаемый ответ : тождества)

Учитель : «Вспомните, как называется тождество cos 2 α + sin 2 α = 1 »

Закрепление изученного материала

А) Учитель: «Откройте учебник стр.147, № 457(2;4)»(вызванные учащиеся решают у доски)

Б) Учитель: «Приступите к выполнению задания №2. Работаем по вариантам» (Обсуждение полученных результатов)

На доске:

1 вариант 2 вариант

Учитель: «В данных формулах перед корнем стоят знаки « ±» . От чего зависит какой знак ставить в формуле?»

(Предполагаемый ответ: «От того, в какой четверти расположен угол поворота точки P(1;0)»)

В) Учитель: «Приступите к выполнению задания №3». (Учащиеся решают задания, проверка на доске)

Подведение итогов урока

Учитель: «Молодцы! Итог урока мы подведем с помощью кроссворда» (Задание 4) (Учащиеся работают в парах за компьютером)

7) Рефлексия в форме анкетирования (приложение 2)

Учитель: «Сделайте вывод о своей работе на уроке, заполнив тест».

8) Домашнее задание

§25, №456, 457(1;3),460(1;3).

Доклад

В этой статье мы всесторонне рассмотрим . Основные тригонометрические тождества представляют собой равенства, устанавливающие связь между синусом, косинусом, тангенсом и котангенсом одного угла, и позволяют находить любую из этих тригонометрических функций через известную другую.

Сразу перечислим основные тригонометрические тождества, которые разберем в этой статье. Запишем их в таблицу, а ниже дадим вывод этих формул и приведем необходимые пояснения.

Навигация по странице.

Связь между синусом и косинусом одного угла

Иногда говорят не об основных тригонометрических тождествах, перечисленных в таблице выше, а об одном единственном основном тригонометрическом тождестве вида . Объяснение этому факту достаточно простое: равенства получаются из основного тригонометрического тождества после деления обеих его частей на и соответственно, а равенства и следуют из определений синуса, косинуса, тангенса и котангенса . Подробнее об этом поговорим в следующих пунктах.

То есть, особый интерес представляет именно равенство , которому и дали название основного тригонометрического тождества.

Прежде чем доказать основное тригонометрическое тождество, дадим его формулировку: сумма квадратов синуса и косинуса одного угла тождественно равна единице. Теперь докажем его.

Основное тригонометрическое тождество очень часто используется при преобразовании тригонометрических выражений . Оно позволяет сумму квадратов синуса и косинуса одного угла заменять единицей. Не менее часто основное тригонометрическое тождество используется и в обратном порядке: единица заменяется суммой квадратов синуса и косинуса какого-либо угла.

Тангенс и котангенс через синус и косинус

Тождества, связывающие тангенс и котангенс с синусом и косинусом одного угла вида и сразу следуют из определений синуса, косинуса, тангенса и котангенса. Действительно, по определению синус есть ордината y, косинус есть абсцисса x, тангенс есть отношение ординаты к абсциссе, то есть, , а котангенс есть отношение абсциссы к ординате, то есть, .

Благодаря такой очевидности тождеств и часто определения тангенса и котангенса дают не через отношение абсциссы и ординаты, а через отношение синуса и косинуса. Так тангенсом угла называют отношение синуса к косинусу этого угла, а котангенсом – отношение косинуса к синусу.

В заключение этого пункта следует отметить, что тождества и имеют место для всех таких углов , при которых входящие в них тригонометрические функции имеют смысл. Так формула справедлива для любых , отличных от (иначе в знаменателе будет нуль, а деление на нуль мы не определяли), а формула - для всех , отличных от , где z - любое .

Связь между тангенсом и котангенсом

Еще более очевидным тригонометрическим тождеством, чем два предыдущих, является тождество, связывающее тангенс и котангенс одного угла вида . Понятно, что оно имеет место для любых углов , отличных от , в противном случае либо тангенс, либо котангенс не определены.

Доказательство формулы очень просто. По определению и , откуда . Можно было доказательство провести и немного иначе. Так как и , то .

Итак, тангенс и котангенс одного угла, при котором они имеют смысл, есть .

Тема: Тригонометрические формулы (25 часов)
Урок 6 – 7: Зависимость между синусом, косинусом и тангенсом одного и того же угла.
Цель: изучить зависимость между синусом, косинусом и тангенсом одного и того же угла. Для достижения поставленной цели необходимо:

Знать:

формулировки определений основных тригонометрических функций (синуса, косинуса и тангенса); знаки тригонометрических функций по четвертям; множество значений тригонометрических функций; основные формулы тригонометрии.

Понимать:

что пользоваться основным тригонометрическим тождеством можно только для одного и того же аргумента; алгоритм вычисления одной тригонометрической функции через другую.

Применить:

умение правильно выбрать нужную формулу для решения конкретного задания; умение работать с простыми дробями; умение выполнять преобразование тригонометрических выражений.

Анализ:

анализировать ошибки в логике рассуждения.

Синтез:

предложить свой способ решения примеров; составить кроссворд, используя полученные знания.

Оценка:

знаний и умений по данной теме для использования в других разделах алгебры.

Оборудование: макет тригонометрической окружности, раздаточный справочный материал с формулами и таблицами значений тригонометрических функций, компьютер, мультимедийный проектор, презентация, листы с заданиями для самостоятельной работы.Ход урока:

Организационный момент.

Приветствие. Сообщение цели урока и плана работы на уроке.

Актуализация знаний и умений.

Учащимся раздаются карты урока и даются пояснения как с ними работать. На экран выводятся вопросы; учащиеся записывают ответы в тетрадь; преподаватель выводит на экран правильный ответ. После окончания опроса учащиеся выставляют баллы в карту урока для Задания № 1.

В какой четверти находится угол в 1 радиан и чему он примерно равен?

(В I четверти, 1 рад. 57,3 0).

Какое слово пропущено в определение функции синус?

Синусом угла  называется............ точки единичной окружности. (Ордината)

Какое слово пропущено в определении функции косинус?

Косинусом угла  называется............ точки единичной окружности (Абсцисса).

Какие значения может принимать синус?

()

Объяснение нового материала.

Изобразим единичную окружность с центром в точке О. Пусть при повороте радиуса ОА, равного R, на угол  получен радиус ОВ (рис. 5). Тогда по определению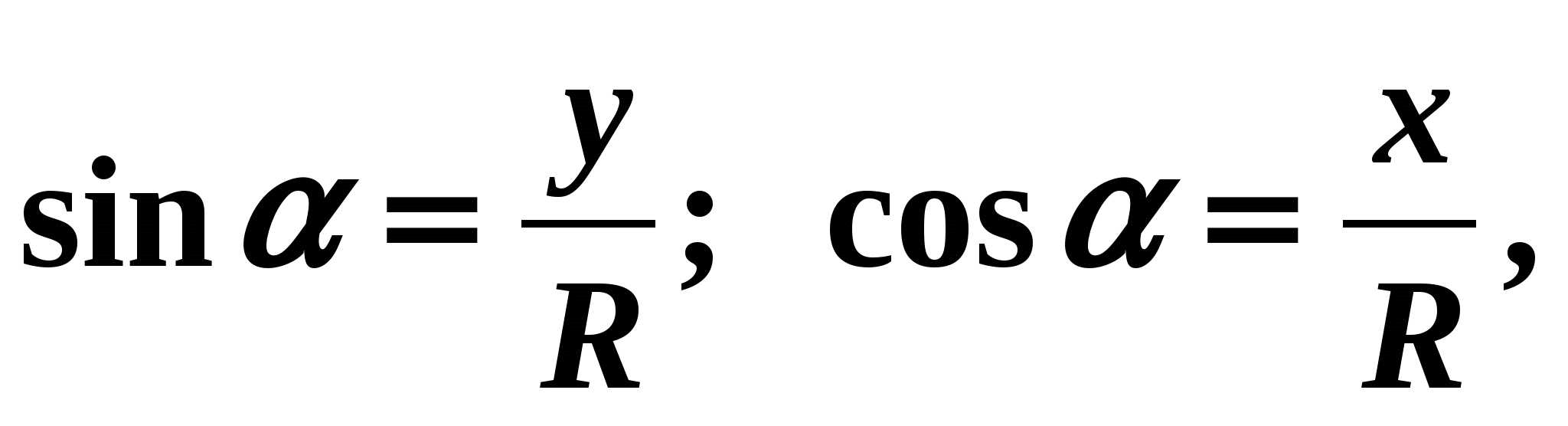
где – абсцисса точки В, – ее ордината. Отсюда следует, что Точка В принадлежит окружности. Поэтому ее координаты удовлетворяют уравнению
Воспользовавшись тем, что получим
(1). Мы получили равенство справедливое при любых значениях входящих в него букв. Как называются такие равенства? Правильно – тождества. Равенство (1) называется основным тригонометрическим тождеством. В равенстве (1)  может принимать любые значения. Самостоятельно завершите запись:
1.
Проверьте правильность вашей записи. Выставите себе баллы в карту урока для Задания № 2. Продолжаем. Мы вывели основное тригонометрическое тождество, а для чего оно нам нужно? Правильно – для нахождения по одному известному нам значению синуса значение косинуса и наоборот. Вот теперь мы с вами всегда сможем пользоваться основным тригонометрическим тождеством, но главное – для одного и того же аргумента. Учащимся в тетради предлагается самостоятельно выразить из основного тригонометрического тождества синус через косинус и косинус через синус. Для проверки к доске вызываются два ученика. Одному предлагается выразить синус через косинус, второму – косинус через синус. На экран выводится верный ответ:
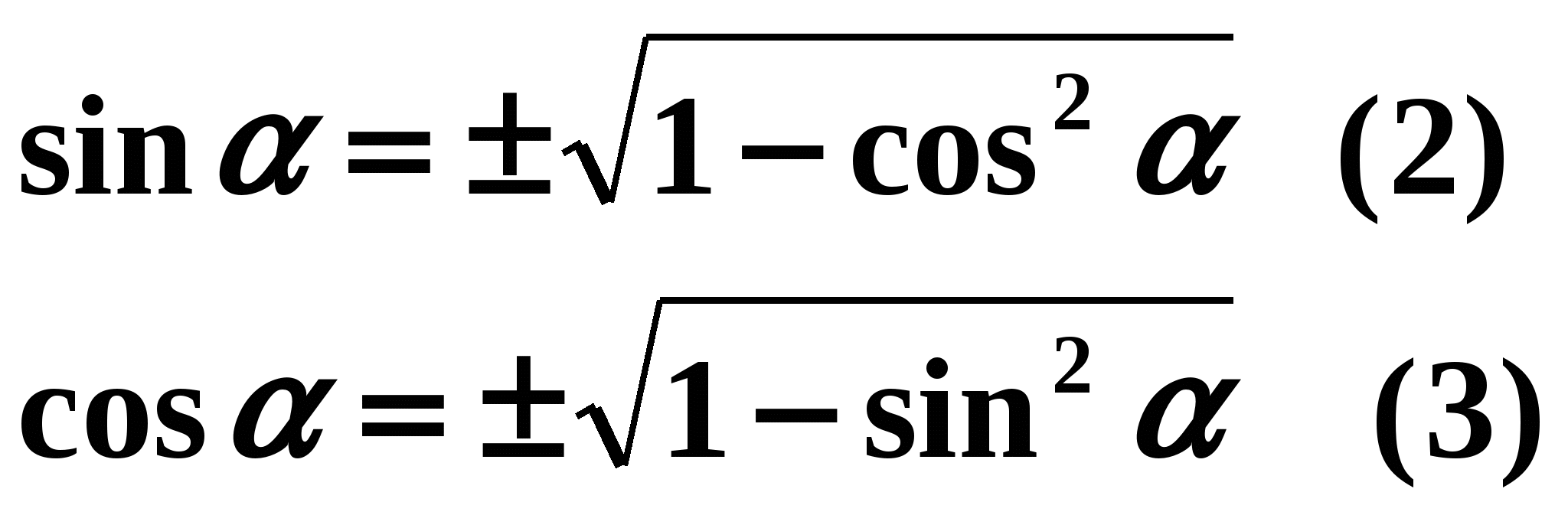Учащиеся проверяют свои ответы и выставляют баллы в карту урока для Задания № 3. В этих формулах от чего зависит знак перед корнем? (От того, в какой четверти расположен угол тригонометрической функции, которую мы определяем).
Пример 1 . Вычислить
если
Определим четверть, в которой находится угол . Четверть – III. Вспомним, что синус в третьей четверти отрицательный, т. е. в формуле (2) перед корнем нужно поставить знак « – »: Пример 2. Вычислить
если
Определяем четверть, в которой находится угол  . Четверть – IV, косинус в четвертой четверти положителен. Поэтому в формуле (3) перед корнем нужен знак « + »:
Выясним теперь зависимость между тангенсом и котангенсом . По определению тангенса и котангенса

Перемножая эти равенства, получаем:


Из равенства (4) можно выразить
через
и наоборот:


Равенства (4) – (6) верны при всех значениях, при которых
имеют смысл, т. е. при
Выведем теперь формулы, выражающие соотношения между тангенсом и косинусом, а также котангенсом и синусом одного и того же аргумента. Разделив обе части равенства (1) на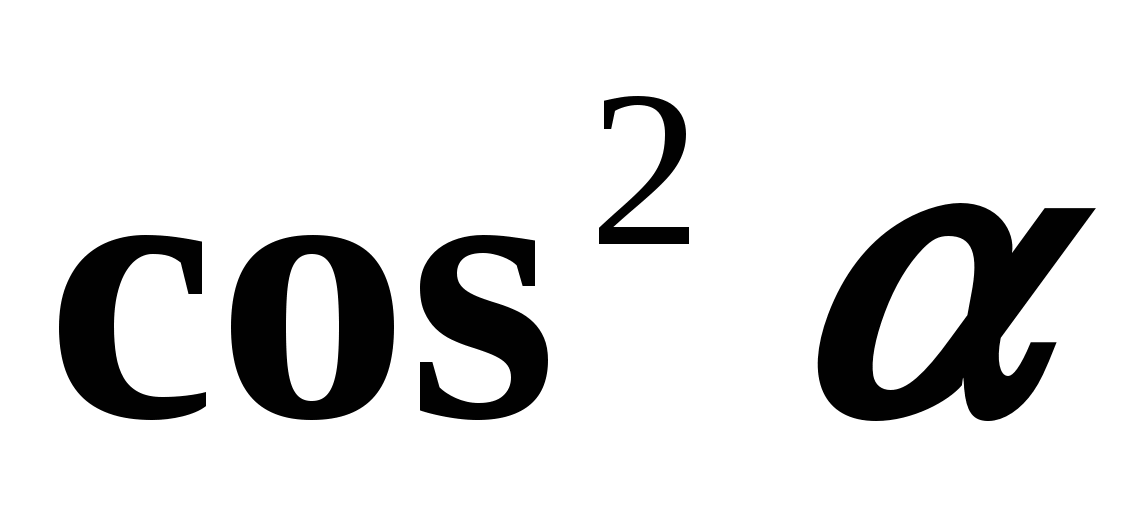
, получим:
т.е.

Если обе части равенства (1) разделить на
, то будем иметь:
т.е.

Рассмотрим примеры использования выведенных формул для нахождения значений тригонометрических функций по известному значению одной из них.
Пример 1. Найдем если известно, что
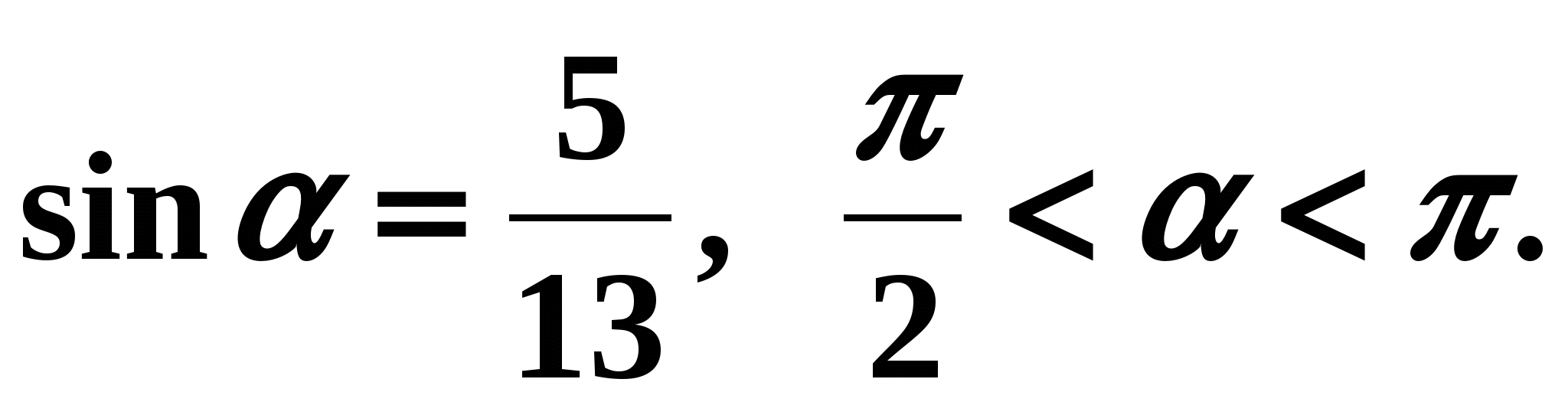Решение:

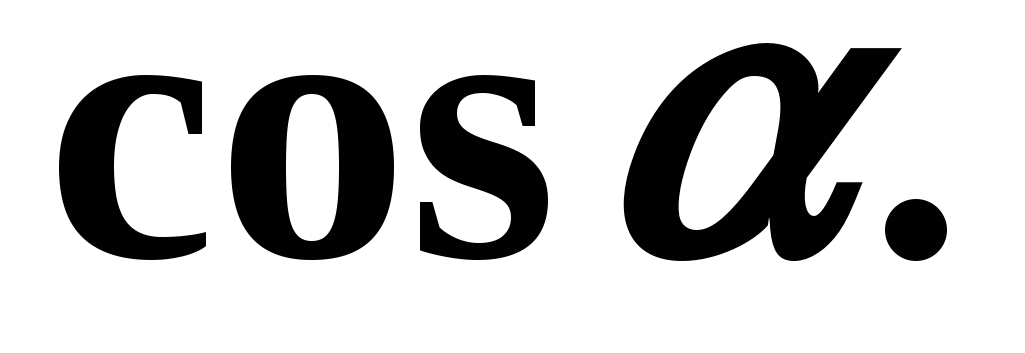
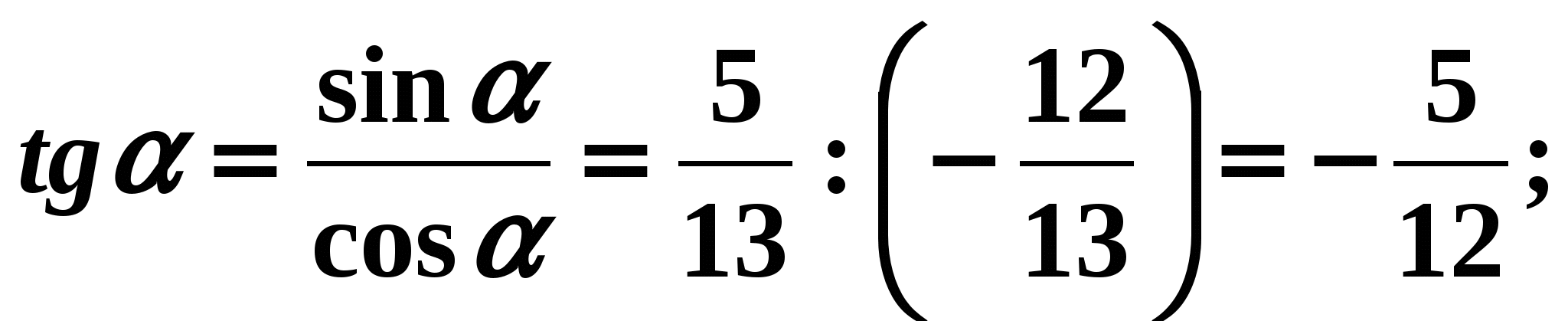
Для отыскания котангенса угла  удобно воспользоваться формулой (6):

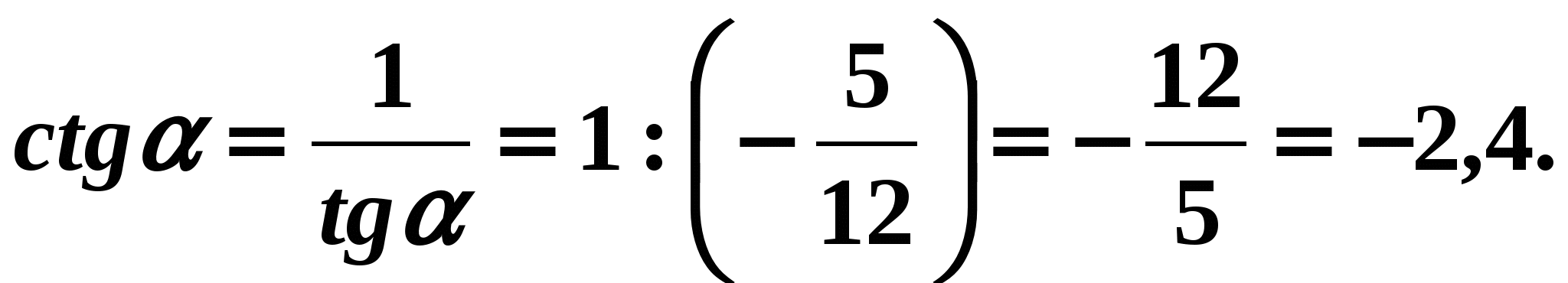Ответ:
Пример2. Известно, что
. Найдем все остальные тригонометрические функции. Решение:

Воспользуемся формулой (7). Имеем:

,
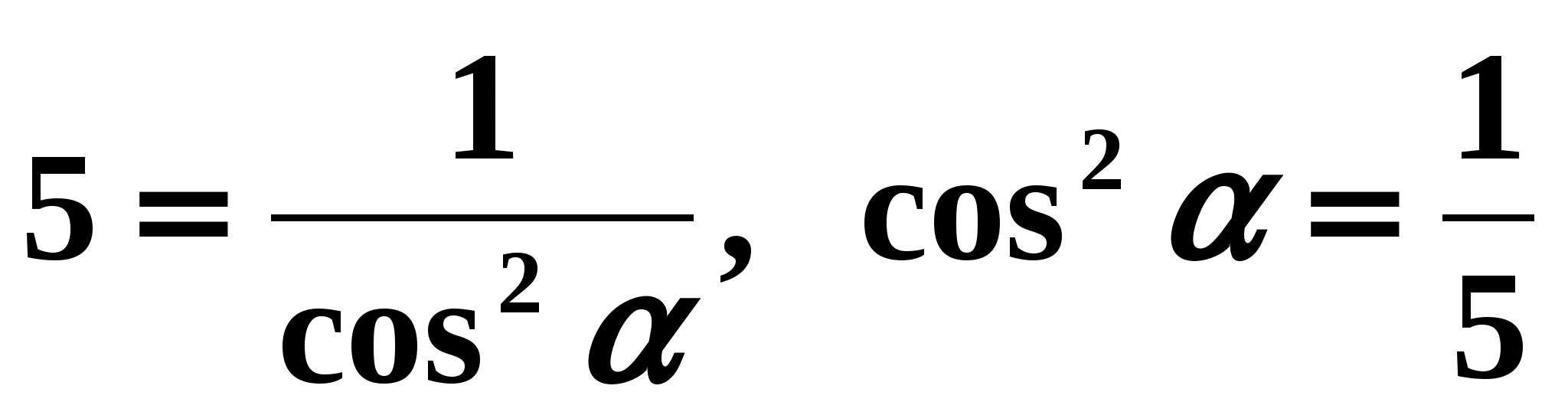. По условию задачи угол  является углом 1 четверти, поэтому его косинус положителен. Значит



Ответ:
Установленные соотношения между тригонометрическими функциями одного и того же аргумента позволяют упрощать тригонометрические выражения.
Пример 3. Упростим выражение:
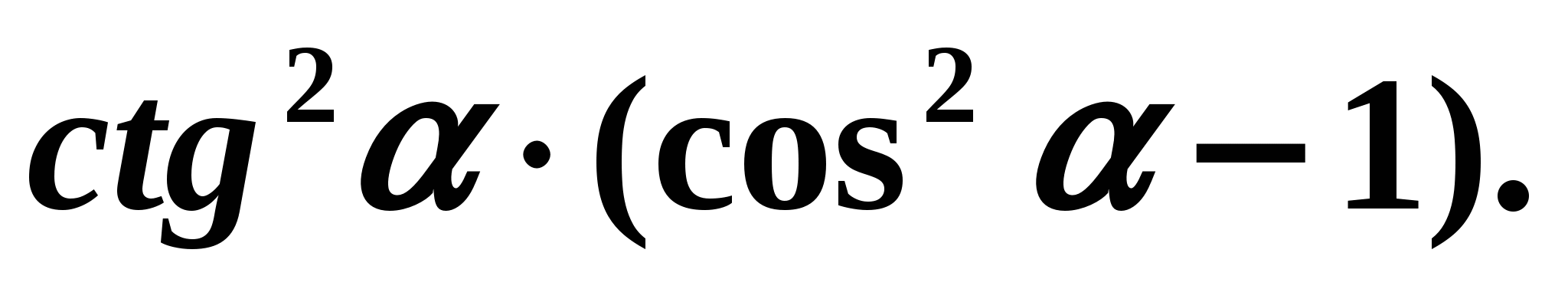Решение: Воспользуемся формулами:
. Получим:

Закрепление.

А сейчас на экране представлены рубрики самооценки по данной теме. Отметьте, на какой уровень вы бы хотели сегодня выйти.

Я понял тему и могу решать примеры по алгоритму, глядя в тетрадь, но с помощью наводящих вопросов (карточка – инструкция).

Я понял тему и могу решать примеры по алгоритму, глядя в тетрадь, используя указания преподавателя.

Я понял тему и могу решать примеры по алгоритму, глядя в тетрадь, без наводящих вопросов и указаний.

Я понял тему и могу решать примеры по алгоритму, не заглядывая в тетрадь.

Какой бы уровень вы не выбрали, сначала внимательно просмотрите все задания, которые я вам раздала, а затем выполните задание, соответствующее выбранному вами уровню (перед вами лежат задания четырех вариантов, номер варианта соответствует уровням самооценки.)

1 вариант

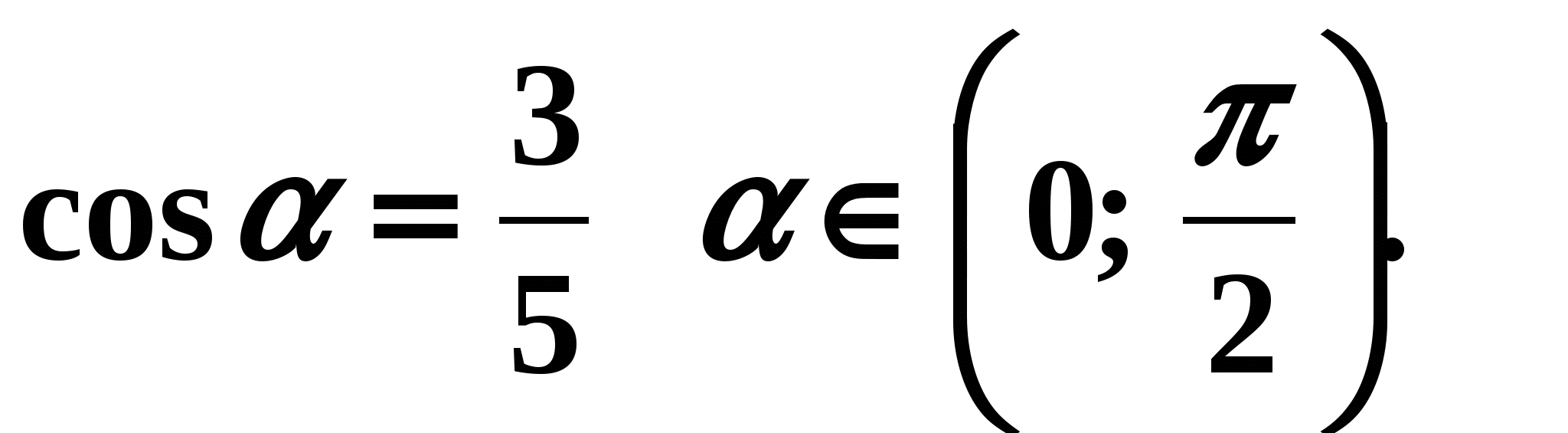Инструкция:

4 вариант

А теперь, ребята, давайте проверим ответы. На экран выводятся правильные ответы, и учащиеся проверяют свои работы и выставляют баллы в карту урока для Задания № 4. По карте урока оцените себя. Подсчитайте свои баллы и выставите их в карту.

Домашнее задание.
Записать все выведенные формулы в справочник. По учебнику №459 (3, 5), №460 (1)

6

«Теорема синусов и косинусов» - 1) Запишите теорему синусов для данного треугольника: Найдите угол В. Запишите формулу для вычисления: Теорема синусов: Найдите длину стороны ВС. Теоремы синусов и косинусов. Стороны треугольника пропорциональны синусам противолежащих углов. 2) Запишите теорему косинусов для вычисления стороны МК: Самостоятельная работа:

«Решение тригонометрических неравенств» - Все значения y на промежутке MN. 1. Строим графики функций: Остальные промежутки. Прямая y=-1/2 пересекает синусоиду в бесконечном числе точек, а тригонометрический круг - в точке А. бесконечного множества промежутков. А на синусоиде, ближайший к началу координат промежуток значений x, при которых sinx>-1/2,

«Тригонометрические формулы» - Формулы преобразования суммы тригонометрических функций в произведение. Формулы преобразования произведения тригонометрических функций в сумму. Формулы сложения. По тригонометрическим функциям угла?. Формулы двойных углов. Сложив почленно равенства (3) и (4), получим: Выведем вспомогательные формулы, позволяющие находить.

«Решение простейших тригонометрических неравенств» - cos x. Методы решения тригонометрических неравенств. sin x. Тригонометрическими неравенствами называются неравенства, содержащие переменную в аргументе тригонометрической функции. Решение простейших тригонометрических неравенств.

«Sin и cos» - Верно ли,что косинус 6,5 больше нуля? Синус 60° равен?? Верно ли что соs? х - siп? х = 1? Раздел математики, изучающий свойства синуса, косинуса… Урок по алгебре и началам анализа в 10 классе. Решение тригонометрических уравнений и неравенств. Абсцисса точки на единичной окружности. Отношение косинуса к синусу…

«Теорема косинусов для треугольника» - Устная работа. Неизвестные элементы. Треугольник. Квадрат стороны треугольника. Сформулируйте теорему косинусов. Теорема. Теорема косинусов. Решение задач на клеточной бумаге. Углы и стороны. Сформулировать теорему косинусов. Задачи по готовым чертежам. Данные, указанные на рисунке.

Всего в теме 21 презентация

Попробуем отыскать зависимость между основными тригонометрическими функциями одного и того же угла.

Соотношение между косинусом и синусом одного и того же угла

На следующем рисунке представлена система координат Оху с изображенной в ней частью единичной полуокружности ACB с центром в точке О. Эта часть является дугой единичной окружности. Единичная окружность описывается уравнением

• x 2 +y 2 =1.

Как уже известно ординату у и абсциссу х можно представить в виде синуса и косинуса угла по следующим формулам:

• sin(a) = у,
• cos(a) = х.

Подставив эти значения в уравнения единичной окружности имеем следующее равенство

• (sin(a)) 2 + (cos(a)) 2 =1,

Данное равенство, выполняется при любых значениях угла а. Оно называется основное тригонометрическое тождество.

Из основного тригонометрического тождества, можно выразить одну функцию через другую.

• sin(a) = ±√(1-(cos(a)) 2),
• cos(a) = ±√(1-(sin(a)) 2).

Знак в правой части этой формулы определяется знаком выражения, которое стоит в левой части этой формулы.

Например.

Вычислить sin(a), если cos(a)=-3/5 и pi

Воспользуемся формулой приведенной выше:

• sin(a) = ±√(1-(cos(a)) 2).

Так как pi

• sin(a) = ±√(1-(cos(a)) 2) = - √(1 – 9/25) = - 4/5.

Соотношение между тангенсом и котангенсом одного и того же угла

Теперь, попробуем найти зависимость, между тангенсом и котангенсов.

По определению tg(a) = sin(a)/cos(a), ctg(a) = cos(a)/sin(a).

Перемножим эти равенства, получим tg(a)*ctg(a) =1.

Из этого равенства можно выразить одну функцию через другую. Получим:

• tg(a) = 1/ctg(a),
• ctg(a) = 1/tg(a).

Следует понимать, что эти равенства справедливы лишь тогда, когда tg и ctg существуют, то есть для любых а, кроме а=k*pi/2, при любом целом k.

Теперь попробуем используя основное тригонометрическое тождество найти зависимости между тангенсом и косинусом.

Поделим основное тригонометрическое тождество, на (cos(a)) 2 . (cos(a) не равен нулю, иначе бы тангенс не существовал бы.

Получим следующее равенство ((sin(a)) 2 + (cos(a)) 2)/ (cos(a)) 2 =1/(cos(a)) 2 .

Разделив почленно получаем:

• 1+(tg(a)) 2 = 1/(cos(a)) 2 .

Как уже отмечалось выше, эта формула верна если cos(a) не равен нулю, то есть для всех углов а, кроме а=pi/2 +pi*k, при любом целом k.