Der mathematische Erwartungswert der Binomialverteilung wird anhand der Formel berechnet. Binomialverteilung: Definition, Formel, Beispiele. Binomialverteilung und Berechnungen in MS Excel

Die Binomialverteilung ist eine der wichtigsten Wahrscheinlichkeitsverteilungen einer diskret variierenden Zufallsvariablen. Die Binomialverteilung ist die Wahrscheinlichkeitsverteilung der Zahl M Eintreten eines Ereignisses A V N voneinander unabhängige Beobachtungen. Oft ein Ereignis A wird als „Erfolg“ einer Beobachtung bezeichnet, und das gegenteilige Ereignis wird als „Misserfolg“ bezeichnet, aber diese Bezeichnung ist sehr bedingt.

Binomialverteilungsbedingungen:

• insgesamt durchgeführt N Prüfungen, in denen die Veranstaltung A kann auftreten oder auch nicht;
• Ereignis A in jedem Versuch kann mit der gleichen Wahrscheinlichkeit auftreten P;
• Tests sind voneinander unabhängig.

Die Wahrscheinlichkeit, dass in N Testveranstaltung A es wird genau kommen M Zeiten, kann mit der Bernoulli-Formel berechnet werden:

,

Wo P- Wahrscheinlichkeit des Eintretens eines Ereignisses A;

Q = 1 - P- die Wahrscheinlichkeit, dass das gegenteilige Ereignis eintritt.

Lass es uns herausfinden Warum hängt die Binomialverteilung in der oben beschriebenen Weise mit der Bernoulli-Formel zusammen? . Ereignis - Anzahl der Erfolge bei N Tests sind in eine Reihe von Optionen unterteilt, bei denen jeweils ein Erfolg erzielt wird M Tests und Misserfolge - in N - M Tests. Betrachten wir eine dieser Optionen: B1 . Mit der Regel zum Addieren von Wahrscheinlichkeiten multiplizieren wir die Wahrscheinlichkeiten entgegengesetzter Ereignisse:

,

und wenn wir bezeichnen Q = 1 - P, Das

.

Jede andere Option, bei der M Erfolg und N - M Misserfolge. Die Anzahl solcher Optionen entspricht der Anzahl der Möglichkeiten, die man haben kann N Testen Sie es M Erfolg.

Summe aller Wahrscheinlichkeiten M Ereignisvorkommensnummern A(Zahlen von 0 bis N) ist gleich eins:

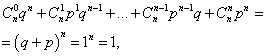
wobei jeder Begriff einen Begriff im Newtonschen Binomial darstellt. Daher wird die betrachtete Verteilung Binomialverteilung genannt.

In der Praxis ist es oft notwendig, Wahrscheinlichkeiten „nicht mehr als“ zu berechnen M Erfolg in N Tests“ oder „zumindest M Erfolg in N Dabei werden die folgenden Formeln verwendet.

Die Integralfunktion also Wahrscheinlichkeit F(M) was drin ist N Beobachtungsereignis A es wird nichts mehr kommen M einmal, kann nach folgender Formel berechnet werden:

Wiederum Wahrscheinlichkeit F(≥M) was drin ist N Beobachtungsereignis A wird nicht weniger kommen M einmal, wird nach der Formel berechnet:

Manchmal ist es bequemer, die Wahrscheinlichkeit dafür zu berechnen N Beobachtungsereignis A es wird nichts mehr kommen M mal durch die Wahrscheinlichkeit des entgegengesetzten Ereignisses:

.

Welche Formel verwendet werden soll, hängt davon ab, bei welcher Formel die Summe weniger Terme enthält.

Die Eigenschaften der Binomialverteilung werden mit den folgenden Formeln berechnet .

Erwarteter Wert: .

Streuung: .

Standardabweichung: .

Binomialverteilung und Berechnungen in MS Excel

Binomiale Wahrscheinlichkeit P N ( M) und die Werte der Integralfunktion F(M) kann mit der MS Excel-Funktion BINOM.VERT berechnet werden. Das Fenster für die entsprechende Berechnung wird unten angezeigt (Linksklick zum Vergrößern).

MS Excel erfordert die Eingabe folgender Daten:

• Anzahl der Erfolge;
• Anzahl der Tests;
• Erfolgswahrscheinlichkeit;
• Integral – logischer Wert: 0 – wenn Sie die Wahrscheinlichkeit berechnen müssen P N ( M) und 1 – wenn die Wahrscheinlichkeit F(M).

Beispiel 1. Der Unternehmensleiter fasste Informationen zur Anzahl der in den letzten 100 Tagen verkauften Kameras zusammen. Die Tabelle fasst die Informationen zusammen und berechnet die Wahrscheinlichkeiten, dass eine bestimmte Anzahl Kameras pro Tag verkauft wird.

Der Tag endet mit einem Gewinn, wenn 13 oder mehr Kameras verkauft werden. Wahrscheinlichkeit, dass der Tag gewinnbringend verläuft:

Wahrscheinlichkeit, dass ein Tag ohne Gewinn gearbeitet wird:

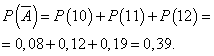
Die Wahrscheinlichkeit, dass an einem Tag mit Gewinn gearbeitet wird, sei konstant und gleich 0,61, und die Anzahl der pro Tag verkauften Kameras sei nicht vom Tag abhängig. Dann können wir die Binomialverteilung verwenden, bei der das Ereignis auftritt A- Der Tag wird mit Gewinn gearbeitet, - ohne Gewinn.

Die Wahrscheinlichkeit, dass alle 6 Tage mit Gewinn abgearbeitet werden:

.

Das gleiche Ergebnis erhalten wir mit der MS Excel-Funktion BINOM.VERT (der Wert des Integralwerts ist 0):

P 6 (6 ) = BINOM.VERT(6; 6; 0,61; 0) = 0,052.

Die Wahrscheinlichkeit, dass von 6 Tagen 4 oder mehr Tage mit Gewinn gearbeitet werden:

Wo ,

,

Mithilfe der MS-Excel-Funktion BINOM.VERT berechnen wir die Wahrscheinlichkeit, dass von 6 Tagen nicht mehr als 3 Tage mit Gewinn abgeschlossen werden (der Wert des Integralwerts beträgt 1):

P 6 (≤3 ) = BINOM.VERT(3; 6; 0,61; 1) = 0,435.

Wahrscheinlichkeit, dass alle 6 Tage mit Verlusten durchgearbeitet werden:

,

Den gleichen Indikator können wir mit der MS Excel-Funktion BINOM.VERT berechnen:

P 6 (0 ) = BINOM.VERT(0; 6; 0,61; 0) = 0,0035.

Lösen Sie das Problem selbst und sehen Sie dann die Lösung

Beispiel 2. In der Urne befinden sich 2 weiße Kugeln und 3 schwarze Kugeln. Eine Kugel wird aus der Urne genommen, die Farbe eingestellt und zurückgelegt. Der Versuch wird 5 Mal wiederholt. Die Häufigkeit des Vorkommens weißer Kugeln ist eine diskrete Zufallsvariable X, verteilt nach dem Binomialgesetz. Erstellen Sie ein Verteilungsgesetz einer Zufallsvariablen. Definieren Sie Modus, mathematische Erwartung und Streuung.

Lassen Sie uns weiterhin gemeinsam Probleme lösen

Beispiel 3. Vom Kurierdienst aus gingen wir zu den Standorten N= 5 Kuriere. Jeder Kurier ist wahrscheinlich P= 0,3, unabhängig von anderen, ist zu spät für das Objekt. Diskrete Zufallsvariable X- Anzahl verspäteter Kuriere. Konstruieren Sie eine Verteilungsreihe für diese Zufallsvariable. Finden Sie den mathematischen Erwartungswert, die Varianz und die Standardabweichung. Ermitteln Sie die Wahrscheinlichkeit, dass mindestens zwei Kuriere zu spät für die Objekte kommen.

In diesem und den nächsten Beiträgen werden wir uns mit mathematischen Modellen zufälliger Ereignisse befassen. Mathematisches Modell ist ein mathematischer Ausdruck, der eine Zufallsvariable darstellt. Für diskrete Zufallsvariablen wird dieser mathematische Ausdruck als Verteilungsfunktion bezeichnet.

Wenn das Problem es Ihnen ermöglicht, explizit einen mathematischen Ausdruck zu schreiben, der eine Zufallsvariable darstellt, können Sie die genaue Wahrscheinlichkeit jedes ihrer Werte berechnen. In diesem Fall können Sie alle Werte der Verteilungsfunktion berechnen und auflisten. In betriebswirtschaftlichen, soziologischen und medizinischen Anwendungen sind unterschiedliche Verteilungen von Zufallsvariablen anzutreffen. Eine der nützlichsten Verteilungen ist die Binomialverteilung.

Binomialverteilung Wird zur Simulation von Situationen verwendet, die durch die folgenden Merkmale gekennzeichnet sind.

• Die Stichprobe besteht aus einer festen Anzahl von Elementen N, das die Ergebnisse eines bestimmten Tests darstellt.
• Jedes Stichprobenelement gehört zu einer von zwei sich gegenseitig ausschließenden Kategorien, die den gesamten Stichprobenraum ausschöpfen. Typischerweise werden diese beiden Kategorien als Erfolg und Misserfolg bezeichnet.
• Erfolgswahrscheinlichkeit R ist konstant. Daher beträgt die Ausfallwahrscheinlichkeit 1 – S.
• Das Ergebnis (d. h. Erfolg oder Misserfolg) eines Versuchs hängt nicht vom Ergebnis eines anderen Versuchs ab. Um die Unabhängigkeit der Ergebnisse sicherzustellen, werden Stichprobenelemente typischerweise mit zwei verschiedenen Methoden ermittelt. Jedes Element in der Stichprobe wird zufällig aus einer unendlichen Grundgesamtheit ohne Umkehrung oder aus einer endlichen Grundgesamtheit mit Umkehrung gezogen.

Laden Sie die Notiz im oder Format herunter, Beispiele im Format

Die Binomialverteilung wird verwendet, um die Anzahl der Erfolge in einer Stichprobe bestehend aus abzuschätzen N Beobachtungen. Nehmen wir als Beispiel die Bestellung. Um eine Bestellung aufzugeben, können Kunden der Saxon Company das interaktive elektronische Formular nutzen und dieses an die Firma senden. Anschließend prüft das Informationssystem die Aufträge auf Fehler, Unvollständigkeiten oder falsche Angaben. Jede betreffende Bestellung wird markiert und in den täglichen Ausnahmebericht aufgenommen. Die vom Unternehmen gesammelten Daten zeigen, dass die Fehlerwahrscheinlichkeit bei Bestellungen 0,1 beträgt. Ein Unternehmen möchte wissen, wie hoch die Wahrscheinlichkeit ist, in einer bestimmten Stichprobe eine bestimmte Anzahl fehlerhafter Bestellungen zu finden. Angenommen, Kunden füllen vier elektronische Formulare aus. Wie hoch ist die Wahrscheinlichkeit, dass alle Bestellungen fehlerfrei sind? Wie berechnet man diese Wahrscheinlichkeit? Unter Erfolg verstehen wir einen Fehler beim Ausfüllen des Formulars, alle anderen Ergebnisse gelten als Fehlschlag. Denken Sie daran, dass wir an der Anzahl fehlerhafter Bestellungen in einer bestimmten Stichprobe interessiert sind.

Welche Ergebnisse können wir beobachten? Wenn die Stichprobe aus vier Bestellungen besteht, können eine, zwei, drei oder alle vier falsch sein, und alle davon können richtig sein. Kann eine Zufallsvariable, die die Anzahl falsch ausgefüllter Formulare beschreibt, einen anderen Wert annehmen? Dies ist nicht möglich, da die Anzahl der fehlerhaften Formulare die Stichprobengröße nicht überschreiten darf N oder negativ sein. Somit nimmt eine Zufallsvariable, die dem Binomialverteilungsgesetz gehorcht, Werte von 0 bis an N.

Nehmen wir an, dass in einer Stichprobe von vier Aufträgen die folgenden Ergebnisse beobachtet werden:

Wie groß ist die Wahrscheinlichkeit, in einer Stichprobe von vier Bestellungen drei fehlerhafte Bestellungen in der angegebenen Reihenfolge zu finden? Da vorläufige Untersuchungen gezeigt haben, dass die Wahrscheinlichkeit eines Fehlers beim Ausfüllen des Formulars 0,10 beträgt, werden die Wahrscheinlichkeiten der oben genannten Ergebnisse wie folgt berechnet:

Da die Ergebnisse nicht voneinander abhängen, ist die Wahrscheinlichkeit der angegebenen Ergebnisfolge gleich: p*p*(1–p)*p = 0,1*0,1*0,9*0,1 = 0,0009. Wenn Sie die Anzahl der Auswahlmöglichkeiten berechnen müssen X N Elemente sollten Sie die Kombinationsformel (1) verwenden:

wo n! = n * (n –1) * (n – 2) * … * 2 * 1 - Fakultät einer Zahl N, und 0! = 1 und 1! = 1 per Definition.

Dieser Ausdruck wird oft als bezeichnet. Wenn also n = 4 und X = 3, wird die Anzahl der Sequenzen, die aus drei Elementen bestehen, die aus einer Stichprobengröße von 4 extrahiert wurden, durch die folgende Formel bestimmt:

Daher wird die Wahrscheinlichkeit, drei fehlerhafte Bestellungen zu erkennen, wie folgt berechnet:

(Anzahl der möglichen Sequenzen) *
(Wahrscheinlichkeit einer bestimmten Sequenz) = 4 * 0,0009 = 0,0036

Ebenso können Sie die Wahrscheinlichkeit berechnen, dass unter vier Bestellungen eine oder zwei fehlerhaft sind, sowie die Wahrscheinlichkeit, dass alle Bestellungen fehlerhaft oder alle korrekt sind. Allerdings mit zunehmender Stichprobengröße N Es wird schwieriger, die Wahrscheinlichkeit einer bestimmten Folge von Ergebnissen zu bestimmen. In diesem Fall sollten Sie das entsprechende mathematische Modell anwenden, das die Binomialverteilung der Anzahl der Auswahlmöglichkeiten beschreibt X Objekte aus einer Auswahl enthalten N Elemente.

Binomialverteilung

Wo P(X)- Wahrscheinlichkeit X Erfolg für eine gegebene Stichprobengröße N und Erfolgswahrscheinlichkeit R, X = 0, 1, … N.

Bitte beachten Sie, dass Formel (2) eine Formalisierung intuitiver Schlussfolgerungen ist. Zufälliger Wert X, das der Binomialverteilung gehorcht, kann jeden ganzzahligen Wert im Bereich von 0 bis annehmen N. Arbeiten RX(1 – p)N – X stellt die Wahrscheinlichkeit dar, dass eine bestimmte Sequenz besteht aus X Erfolg bei einer Stichprobengröße gleich N. Der Wert bestimmt die Anzahl der möglichen Kombinationen bestehend aus X Erfolg in N Tests. Daher für eine bestimmte Anzahl von Tests N und Erfolgswahrscheinlichkeit R Wahrscheinlichkeit einer Folge bestehend aus X Erfolg, gleich

P(X) = (Anzahl möglicher Sequenzen) * (Wahrscheinlichkeit einer bestimmten Sequenz) =

Betrachten wir Beispiele, die die Anwendung der Formel (2) veranschaulichen.

1. Nehmen wir an, dass die Wahrscheinlichkeit, das Formular falsch auszufüllen, 0,1 beträgt. Wie hoch ist die Wahrscheinlichkeit, dass von vier ausgefüllten Formularen drei falsch sind? Mithilfe der Formel (2) finden wir heraus, dass die Wahrscheinlichkeit, drei fehlerhafte Bestellungen in einer Stichprobe bestehend aus vier Bestellungen zu erkennen, gleich ist

2. Nehmen wir an, dass die Wahrscheinlichkeit, das Formular falsch auszufüllen, 0,1 beträgt. Wie groß ist die Wahrscheinlichkeit, dass von vier ausgefüllten Formularen mindestens drei falsch sind? Wie im vorherigen Beispiel gezeigt, beträgt die Wahrscheinlichkeit, dass von vier ausgefüllten Formularen drei falsch sind, 0,0036. Um die Wahrscheinlichkeit zu berechnen, dass von vier ausgefüllten Formularen mindestens drei falsch sind, müssen Sie die Wahrscheinlichkeit, dass von vier ausgefüllten Formularen drei falsch sind, und die Wahrscheinlichkeit, dass von vier ausgefüllten Formularen alle falsch sind, addieren. Die Wahrscheinlichkeit des zweiten Ereignisses beträgt

Somit ist die Wahrscheinlichkeit, dass von vier ausgefüllten Formularen mindestens drei falsch sind, gleich

P(X > 3) = P(X = 3) + P(X = 4) = 0,0036 + 0,0001 = 0,0037

3. Nehmen wir an, dass die Wahrscheinlichkeit, das Formular falsch auszufüllen, 0,1 beträgt. Wie groß ist die Wahrscheinlichkeit, dass von vier ausgefüllten Formularen weniger als drei falsch sind? Wahrscheinlichkeit dieses Ereignisses

P(X< 3) = P(X = 0) + P(X = 1) + P(X = 2)

Mit Formel (2) berechnen wir jede dieser Wahrscheinlichkeiten:

Daher ist P(X< 3) = 0,6561 + 0,2916 + 0,0486 = 0,9963.

Wahrscheinlichkeit P(X< 3) можно вычислить иначе. Для этого воспользуемся тем, что событие X < 3 является дополнительным по отношению к событию Х>3. Dann P(X< 3) = 1 – Р(Х> 3) = 1 – 0,0037 = 0,9963.

Mit zunehmender Stichprobengröße N Berechnungen ähnlich denen in Beispiel 3 werden schwierig. Um diese Komplikationen zu vermeiden, werden viele Binomialwahrscheinlichkeiten im Voraus tabellarisch aufgeführt. Einige dieser Wahrscheinlichkeiten sind in Abb. dargestellt. 1. Zum Beispiel, um die Wahrscheinlichkeit dafür zu ermitteln X= 2 bei N= 4 und P= 0,1, sollten Sie aus der Tabelle die Zahl am Schnittpunkt der Linie extrahieren X= 2 und Spalten R = 0,1.

Reis. 1. Binomialwahrscheinlichkeit bei N = 4, X= 2 und R = 0,1

Die Binomialverteilung kann mit der Excel-Funktion =BINOM.DIST() (Abb. 2) berechnet werden, die über 4 Parameter verfügt: Anzahl der Erfolge - X, Anzahl der Tests (oder Stichprobengröße) – N, Erfolgswahrscheinlichkeit – R, Parameter Integral, der den Wert TRUE annimmt (in diesem Fall wird die Wahrscheinlichkeit berechnet). nicht weniger X Ereignisse) oder FALSCH (in diesem Fall wird die Wahrscheinlichkeit berechnet). genau X Veranstaltungen).

Reis. 2. Funktionsparameter =BINOM.DIST()

Für die oben genannten drei Beispiele sind die Berechnungen in Abb. dargestellt. 3 (siehe auch Excel-Datei). Jede Spalte enthält eine Formel. Die Zahlen zeigen die Antworten auf die Beispiele der entsprechenden Zahl).

Reis. 3. Berechnung der Binomialverteilung in Excel für N= 4 und P = 0,1

Eigenschaften der Binomialverteilung

Die Binomialverteilung hängt von Parametern ab N Und R. Die Binomialverteilung kann entweder symmetrisch oder asymmetrisch sein. Wenn p = 0,05, ist die Binomialverteilung unabhängig vom Wert des Parameters symmetrisch N. Wenn jedoch p ≠ 0,05, wird die Verteilung schief. Je näher der Parameterwert liegt R auf 0,05 und je größer die Stichprobengröße N, desto weniger ausgeprägt ist die Asymmetrie der Verteilung. Somit ist die Verteilung der Anzahl falsch ausgefüllter Formulare rechtsschief, weil P= 0,1 (Abb. 4).

Reis. 4. Histogramm der Binomialverteilung bei N= 4 und P = 0,1

Erwartung einer Binomialverteilung gleich dem Produkt der Stichprobengröße Nüber die Erfolgswahrscheinlichkeit R:

(3) M = E(X) =n.p.

Im Durchschnitt kann es bei einer ausreichend langen Testreihe in einer Stichprobe bestehend aus vier Aufträgen zu p = E(X) = 4 x 0,1 = 0,4 fehlerhaft ausgefüllten Formularen kommen.

Standardabweichung der Binomialverteilung

Die Standardabweichung der Anzahl falsch ausgefüllter Formulare in einem Buchhaltungsinformationssystem beträgt beispielsweise:

Es werden Materialien aus dem Buch „Statistics for Managers“ von Levin et al. verwendet. – M.: Williams, 2004. – S. 307–313

Grüße an alle Leser!

Wie wir wissen, befasst sich die statistische Analyse mit der Erhebung und Verarbeitung realer Daten. Das Geschäft ist nützlich und oft profitabel, weil... Richtige Schlussfolgerungen ermöglichen es Ihnen, Fehler und Verluste in der Zukunft zu vermeiden und manchmal genau diese Zukunft richtig einzuschätzen. Die gesammelten Daten spiegeln den Zustand einiger beobachteter Phänomene wider. Daten sind oft (aber nicht immer) numerisch und können mathematisch manipuliert werden, um zusätzliche Informationen zu extrahieren.

Allerdings werden nicht alle Phänomene auf einer quantitativen Skala wie 1, 2, 3 ... 100500 ... gemessen. Ein Phänomen kann nicht immer unendlich viele verschiedene Zustände annehmen. Beispielsweise kann das Geschlecht einer Person entweder M oder F sein. Der Schütze trifft entweder das Ziel oder verfehlt es. Sie können entweder „Dafür“ oder „Dagegen“ usw. stimmen. usw. Mit anderen Worten, solche Daten spiegeln den Status eines alternativen Attributs wider – entweder „Ja“ (das Ereignis ist eingetreten) oder „Nein“ (das Ereignis ist nicht eingetreten). Das eintretende Ereignis (positiver Ausgang) wird auch „Erfolg“ genannt. Solche Phänomene können auch weit verbreitet und zufällig sein. Daher können sie gemessen und statistisch valide Schlussfolgerungen gezogen werden.

Experimente mit solchen Daten werden aufgerufen Bernoulli-Schema, zu Ehren des berühmten Schweizer Mathematikers, der herausfand, dass bei einer großen Anzahl von Versuchen das Verhältnis der positiven Ergebnisse zur Gesamtzahl der Versuche tendenziell zur Wahrscheinlichkeit des Eintretens dieses Ereignisses tendiert.

Alternative charakteristische Variable

Um bei der Analyse mathematische Hilfsmittel nutzen zu können, sollten die Ergebnisse solcher Beobachtungen in numerischer Form aufgezeichnet werden. Dazu wird einem positiven Ergebnis die Zahl 1 zugewiesen, einem negativen Ergebnis die Zahl 0. Mit anderen Worten: Wir haben es mit einer Variablen zu tun, die nur zwei Werte annehmen kann: 0 oder 1.

Welchen Nutzen lässt sich daraus ziehen? Eigentlich nicht weniger als aus gewöhnlichen Daten. Daher ist es einfach, die Anzahl der positiven Ergebnisse zu berechnen – summieren Sie einfach alle Werte, d. h. alle 1 (Erfolg). Sie können noch weiter gehen, aber dazu müssen Sie einige Notationen einführen.

Zunächst ist zu beachten, dass positive Ergebnisse (die gleich 1 sind) mit einer gewissen Wahrscheinlichkeit eintreten. Wenn man zum Beispiel beim Werfen einer Münze „Kopf“ erhält, beträgt die Quote ½ oder 0,5. Diese Wahrscheinlichkeit wird traditionell mit dem lateinischen Buchstaben bezeichnet P. Daher ist die Wahrscheinlichkeit für das Eintreten eines alternativen Ereignisses gleich 1 - S, was auch mit bezeichnet wird Q, also q = 1 – p. Diese Notationen können in Form einer Variablenverteilungstabelle übersichtlich systematisiert werden X.

Jetzt haben wir eine Liste möglicher Werte und deren Wahrscheinlichkeiten. Wir können damit beginnen, so bemerkenswerte Eigenschaften einer Zufallsvariablen zu berechnen wie erwarteter Wert Und Streuung. Ich möchte Sie daran erinnern, dass der mathematische Erwartungswert als Summe der Produkte aller möglichen Werte und ihrer entsprechenden Wahrscheinlichkeiten berechnet wird:

Berechnen wir die Erwartung anhand der Notation in den obigen Tabellen.

Es stellt sich heraus, dass die mathematische Erwartung eines alternativen Vorzeichens gleich der Wahrscheinlichkeit dieses Ereignisses ist - P.

Definieren wir nun die Varianz eines alternativen Attributs. Ich möchte Sie auch daran erinnern, dass die Streuung das durchschnittliche Quadrat der Abweichungen von der mathematischen Erwartung ist. Die allgemeine Formel (für diskrete Daten) lautet:

Daher die Varianz des Alternativattributs:

Es ist leicht zu erkennen, dass diese Streuung maximal 0,25 (mit) beträgt p=0,5).

Die Standardabweichung ist die Wurzel der Varianz:

Der Maximalwert überschreitet nicht 0,5.

Wie Sie sehen, haben sowohl der mathematische Erwartungswert als auch die Varianz des alternativen Attributs eine sehr kompakte Form.

Binomialverteilung einer Zufallsvariablen

Betrachten wir die Situation nun aus einem anderen Blickwinkel. Wen interessiert es tatsächlich, dass der durchschnittliche Kopfverlust pro Wurf 0,5 beträgt? Es ist unmöglich, es sich überhaupt vorzustellen. Interessanter ist es, die Frage nach der Anzahl der Köpfe zu stellen, die bei einer bestimmten Anzahl von Würfen erscheinen.

Mit anderen Worten: Der Forscher interessiert sich oft für die Wahrscheinlichkeit des Eintretens einer bestimmten Anzahl erfolgreicher Ereignisse. Dies kann die Anzahl fehlerhafter Produkte in der getesteten Charge (1 – fehlerhaft, 0 – gut) oder die Anzahl der Wiederherstellungen (1 – gesund, 0 – krank) usw. sein. Die Anzahl solcher „Erfolge“ entspricht der Summe aller Werte der Variablen X, d.h. Anzahl der Einzelergebnisse.

Zufälliger Wert B heißt Binomial und nimmt Werte von 0 bis an N(bei B= 0 - alle Teile sind geeignet, mit B = N– alle Teile sind defekt). Es wird davon ausgegangen, dass alle Werte X unabhängig voneinander. Betrachten wir die Hauptmerkmale einer Binomialvariablen, das heißt, wir ermitteln ihren mathematischen Erwartungswert, ihre Streuung und ihre Verteilung.

Der Erwartungswert einer Binomialvariablen ist sehr einfach zu ermitteln. Denken wir daran, dass es für jeden Mehrwert eine Summe mathematischer Erwartungen gibt, die für alle gleich ist. Deshalb:

Beispielsweise beträgt die mathematische Erwartung für die Anzahl der fallengelassenen Köpfe bei 100 Würfen 100 × 0,5 = 50.

Nun leiten wir die Formel für die Dispersion einer Binomialvariablen ab. ist die Summe der Varianzen. Von hier

Standardabweichung bzw

Für 100 Münzwürfe beträgt die Standardabweichung

Betrachten Sie abschließend die Verteilung des Binomialwerts, d. h. die Wahrscheinlichkeit, dass die Zufallsvariable B wird unterschiedliche Werte annehmen k, Wo 0≤k≤n. Bei einer Münze könnte dieses Problem so aussehen: Wie groß ist die Wahrscheinlichkeit, bei 100 Würfen 40 Mal „Kopf“ zu bekommen?

Um die Berechnungsmethode zu verstehen, stellen Sie sich vor, dass die Münze nur viermal geworfen wird. Es kann jedes Mal passieren, dass beide Seiten ausfallen. Wir fragen uns: Wie groß ist die Wahrscheinlichkeit, bei 4 Würfen 2 Köpfe zu bekommen? Jeder Wurf ist unabhängig voneinander. Das bedeutet, dass die Wahrscheinlichkeit, eine beliebige Kombination zu erhalten, dem Produkt der Wahrscheinlichkeiten eines bestimmten Ergebnisses für jeden einzelnen Wurf entspricht. Seien O Kopf und P Zahl. Dann könnte zum Beispiel eine der für uns passenden Kombinationen wie OOPP aussehen, also:

Die Wahrscheinlichkeit einer solchen Kombination ist gleich dem Produkt aus zwei Wahrscheinlichkeiten, „Kopf“ zu bekommen, und zwei weiteren Wahrscheinlichkeiten, „Kopf“ zu bekommen (das umgekehrte Ereignis, berechnet als). 1 - S), d.h. 0,5×0,5×(1-0,5)×(1-0,5)=0,0625. Dies ist die Wahrscheinlichkeit einer der Kombinationen, die zu uns passt. Bei der Frage ging es jedoch um die Gesamtzahl der Adler und nicht um eine bestimmte Reihenfolge. Dann müssen Sie die Wahrscheinlichkeiten aller Kombinationen addieren, in denen es genau 2 Köpfe gibt. Offensichtlich sind sie alle gleich (das Produkt ändert sich nicht, wenn die Faktoren geändert werden). Daher müssen Sie ihre Anzahl berechnen und sie dann mit der Wahrscheinlichkeit einer solchen Kombination multiplizieren. Zählen wir alle Kombinationen von 4 Würfen mit 2 Köpfen: RROO, RORO, ROOR, ORRO, OROR, OORR. Insgesamt gibt es 6 Optionen.

Daher beträgt die gewünschte Wahrscheinlichkeit, nach 4 Würfen 2 Köpfe zu bekommen, 6×0,0625=0,375.

Allerdings ist das Zählen auf diese Weise mühsam. Bereits für 10 Münzen wird es sehr schwierig sein, mit roher Gewalt die Gesamtzahl der Optionen zu erhalten. Deshalb haben kluge Köpfe vor langer Zeit eine Formel erfunden, mit der sie die Anzahl der verschiedenen Kombinationen berechnen können N Elemente von k, Wo N– Gesamtzahl der Elemente, k– die Anzahl der Elemente, deren Anordnungsmöglichkeiten berechnet werden. Formelkombination von N Elemente von k ist das:

Ähnliche Dinge passieren im Abschnitt Kombinatorik. Ich schicke jeden dorthin, der sein Wissen verbessern möchte. Daher übrigens auch der Name der Binomialverteilung (die obige Formel ist ein Koeffizient in der Entwicklung der Newtonschen Binomialverteilung).

Die Formel zur Bestimmung der Wahrscheinlichkeit lässt sich leicht auf jede beliebige Größe verallgemeinern N Und k. Infolgedessen hat die Formel für die Binomialverteilung die folgende Form.

In Worten: die Anzahl der Kombinationen, die die Bedingung erfüllen, multipliziert mit der Wahrscheinlichkeit einer davon.

Für die praktische Anwendung reicht es aus, die Formel der Binomialverteilung zu kennen. Oder Sie wissen es vielleicht noch nicht einmal – im Folgenden zeigen wir, wie Sie die Wahrscheinlichkeit mit Excel ermitteln. Aber es ist besser zu wissen.

Mit dieser Formel berechnen wir die Wahrscheinlichkeit, bei 100 Würfen 40 Köpfe zu erzielen:

Oder nur 1,08 %. Zum Vergleich: Die Wahrscheinlichkeit der mathematischen Erwartung dieses Experiments, also 50 Köpfe, beträgt 7,96 %. Die maximale Wahrscheinlichkeit eines Binomialwerts gehört zu dem Wert, der der mathematischen Erwartung entspricht.

Berechnung der Wahrscheinlichkeit einer Binomialverteilung in Excel

Wenn Sie nur Papier und einen Taschenrechner verwenden, sind Berechnungen mit der Binomialverteilungsformel trotz des Fehlens von Integralen recht schwierig. Der Wert ist beispielsweise 100! – hat mehr als 150 Zeichen. Eine manuelle Berechnung ist nicht möglich. Früher und heute werden zur Berechnung solcher Größen Näherungsformeln verwendet. Derzeit empfiehlt sich der Einsatz spezieller Software, beispielsweise MS Excel. Somit kann jeder Benutzer (auch ein ausgebildeter Humanist) leicht die Wahrscheinlichkeit des Wertes einer binomialverteilten Zufallsvariablen berechnen.

Zur Konsolidierung des Materials verwenden wir vorerst Excel als regulären Taschenrechner, d.h. Führen wir eine schrittweise Berechnung mit der Binomialverteilungsformel durch. Berechnen wir zum Beispiel die Wahrscheinlichkeit, 50 Köpfe zu bekommen. Unten sehen Sie ein Bild mit den Berechnungsschritten und dem Endergebnis.

Wie Sie sehen, sind die Zwischenergebnisse so groß, dass sie nicht in eine Zelle passen, obwohl einfache Funktionen wie FACTOR (eine Fakultät berechnen), POWER (eine Zahl potenzieren) sowie Multiplikations- und Divisionsoperatoren funktionieren werden überall verwendet. Außerdem ist diese Berechnung ziemlich umständlich; auf jeden Fall ist sie nicht kompakt, weil Viele Zellen sind beteiligt. Ja, und es ist ein wenig schwierig, es auf Anhieb herauszufinden.

Im Allgemeinen stellt Excel eine vorgefertigte Funktion zur Berechnung der Wahrscheinlichkeiten einer Binomialverteilung bereit. Die Funktion heißt BINOM.VERT.

Anzahl der Erfolge– Anzahl erfolgreicher Tests. Wir haben 50 davon.

Anzahl der Tests– Anzahl der Würfe: 100 Mal.

Erfolgswahrscheinlichkeit– Die Wahrscheinlichkeit, bei einem Wurf „Kopf“ zu bekommen, beträgt 0,5.

Integral– Es wird entweder 1 oder 0 angezeigt. Wenn 0, dann wird die Wahrscheinlichkeit berechnet P(B=k); wenn 1, dann wird die Binomialverteilungsfunktion berechnet, d.h. die Summe aller Wahrscheinlichkeiten aus B=0 Vor B=k inklusive.

Klicken Sie auf OK und erhalten Sie das gleiche Ergebnis wie oben, nur dass alles mit einer Funktion berechnet wurde.

Sehr bequem. Aus Versuchsgründen setzen wir anstelle des letzten Parameters 0 1 ein. Wir erhalten 0,5398. Das bedeutet, dass bei 100 Münzwürfen die Wahrscheinlichkeit, Kopf zwischen 0 und 50 zu bekommen, bei fast 54 % liegt. Aber zunächst schien es, als müssten es 50 % sein. Im Allgemeinen erfolgen Berechnungen schnell und einfach.

Ein echter Analyst muss verstehen, wie sich die Funktion verhält (wie ist ihre Verteilung), also berechnen wir die Wahrscheinlichkeiten für alle Werte von 0 bis 100. Das heißt, wir stellen die Frage: Wie hoch ist die Wahrscheinlichkeit, dass kein einziger Kopf vorhanden ist? erscheint, dass 1 Adler erscheint, 2, 3, 50, 90 oder 100. Die Berechnung ist im folgenden selbstbewegten Bild dargestellt. Die blaue Linie ist die Binomialverteilung selbst, der rote Punkt ist die Wahrscheinlichkeit für eine bestimmte Anzahl an Erfolgen k.

Man könnte sich fragen, ob die Binomialverteilung ähnlich ist wie ... Ja, sehr ähnlich. Sogar Moivre (im Jahr 1733) sagte, dass die Binomialverteilung mit großen Stichproben näherkommt (ich weiß nicht, wie sie damals hieß), aber niemand hörte ihm zu. Erst Gauß und 60–70 Jahre später Laplace entdeckten das Normalverteilungsgesetz wieder und untersuchten es sorgfältig. Die obige Grafik zeigt deutlich, dass die maximale Wahrscheinlichkeit auf der mathematischen Erwartung liegt und bei Abweichung davon stark abnimmt. Genau wie das normale Gesetz.

Die Binomialverteilung ist von großer praktischer Bedeutung und kommt recht häufig vor. Mit Excel lassen sich Berechnungen schnell und einfach durchführen. So können Sie es sicher verwenden.

Damit schlage ich vor, mich bis zum nächsten Treffen zu verabschieden. Alles Gute, bleiben Sie gesund!

Wahrscheinlichkeitsverteilungen diskreter Zufallsvariablen. Binomialverteilung. Poisson-Verteilung. Geometrische Verteilung. Generierende Funktion.

6. Wahrscheinlichkeitsverteilungen diskreter Zufallsvariablen

6.1. Binomialverteilung

Lass es entstehen N unabhängige Prüfungen, in denen jeweils die Veranstaltung A Es kann erscheinen oder auch nicht. Wahrscheinlichkeit P Eintreten eines Ereignisses A ist in allen Tests konstant und ändert sich nicht von Test zu Test. Betrachten Sie als Zufallsvariable X die Häufigkeit des Auftretens des Ereignisses A in diesen Tests. Formel zur Ermittlung der Wahrscheinlichkeit des Eintretens eines Ereignisses A glatt k einmal alle N Tests werden bekanntlich beschrieben Bernoullis Formel

Die durch die Bernoulli-Formel definierte Wahrscheinlichkeitsverteilung heißt Binomial- .

Dieses Gesetz wird „Binomial“ genannt, weil die rechte Seite als allgemeiner Term bei der Entwicklung des Newtonschen Binomials betrachtet werden kann

Schreiben wir das Binomialgesetz in Form einer Tabelle

	P N	n.p. N –1 Q				Q N

Lassen Sie uns die numerischen Eigenschaften dieser Verteilung ermitteln.

Per Definition der mathematischen Erwartung für den DSV gilt:

.

Schreiben wir die Gleichheit auf, die eine Binärzahl von Newton ist

.

und differenzieren Sie es nach p. Als Ergebnis erhalten wir

.

Multiplizieren Sie die linke und rechte Seite mit P:

.

Bedenkt, dass P+ Q=1, wir haben

(6.2)

Also, mathematische Erwartung der Häufigkeit des Auftretens von Ereignissen inNUnabhängige Versuche sind gleich dem Produkt aus der Anzahl der VersucheNauf WahrscheinlichkeitPAuftreten eines Ereignisses in jedem Versuch.

Berechnen wir die Varianz mithilfe der Formel

.

Dafür werden wir finden

.

Lassen Sie uns zunächst die Newtonsche Binomialformel zweimal nach differenzieren P:

und multipliziere beide Seiten der Gleichheit mit P 2:

Somit,

Die Varianz der Binomialverteilung beträgt also

. (6.3)

Diese Ergebnisse können auch aus rein qualitativen Überlegungen gewonnen werden. Die Gesamtzahl X des Auftretens von Ereignis A über alle Versuche hinweg ist die Summe der Häufigkeit des Auftretens des Ereignisses in einzelnen Versuchen. Wenn also X 1 die Anzahl der Vorkommnisse des Ereignisses im ersten Versuch ist, X 2 – im zweiten usw., dann ist die Gesamtzahl der Vorkommnisse von Ereignis A in allen Versuchen gleich X = X 1 +X 2 +…+X N. Gemäß der Eigenschaft der mathematischen Erwartung:

Jeder der Terme auf der rechten Seite der Gleichung ist die mathematische Erwartung der Anzahl von Ereignissen in einem Versuch, die gleich der Wahrscheinlichkeit des Ereignisses ist. Auf diese Weise,

Gemäß der Dispersionseigenschaft:

Da und der mathematische Erwartungswert einer Zufallsvariablen , die nur zwei Werte annehmen kann, nämlich 1 2 mit Wahrscheinlichkeit P und 0 2 mit Wahrscheinlichkeit Q, Das
. Auf diese Weise,
Als Ergebnis erhalten wir

Mit dem Konzept der Anfangs- und Zentralmomente können wir Formeln für Asymmetrie und Kurtosis erhalten:

. (6.4)

Reis. 6.1

Das Polygon der Binomialverteilung hat die folgende Form (siehe Abb. 6.1). WahrscheinlichkeitP N (k) nimmt zunächst mit zunehmender Größe zu k, erreicht seinen höchsten Wert und beginnt dann zu sinken. Die Binomialverteilung ist bis auf diesen Fall schief P=0,5. Beachten Sie das bei einer großen Anzahl von Tests N Die Binomialverteilung kommt der Normalverteilung sehr nahe. (Die Begründung für diesen Vorschlag hängt mit dem lokalen Theorem von Moivre-Laplace zusammen.)

NummerM 0 das Eintreten eines Ereignisses wird genannthöchstwahrscheinlich , wenn die Wahrscheinlichkeit, dass ein Ereignis in dieser Testreihe eine bestimmte Anzahl von Malen auftritt, am größten ist (Maximum im Verteilungspolygon). Für Binomialverteilung

Kommentar. Diese Ungleichheit lässt sich mit der wiederkehrenden Formel für Binomialwahrscheinlichkeiten beweisen:

(6.6)

Beispiel 6.1. Der Anteil an Premiumprodukten beträgt bei diesem Unternehmen 31 %. Wie hoch sind der mathematische Erwartungswert und die Varianz sowie die wahrscheinlichste Anzahl an Premiumprodukten in einer zufällig ausgewählten Charge von 75 Produkten?

Lösung. Weil das P=0,31, Q=0,69, N=75 also

M[ X] = n.p.= 750,31 = 23,25; D[ X] = npq = 750,310,69 = 16,04.

Um die wahrscheinlichste Zahl zu finden M 0, erstellen wir eine doppelte Ungleichung

Es folgt dem M 0 = 23.

Guten Tag! Wir wissen bereits, was eine Wahrscheinlichkeitsverteilung ist. Sie kann diskret oder kontinuierlich sein, und wir haben gelernt, dass sie Wgenannt wird. Schauen wir uns nun ein paar gängigere Distributionen an. Nehmen wir an, ich habe eine Münze, noch dazu eine faire Münze, und ich werde sie fünfmal werfen. Ich werde auch eine Zufallsvariable X definieren, die mit einem Großbuchstaben X gekennzeichnet ist. Sie entspricht der Anzahl der Köpfe bei 5 Würfen. Vielleicht habe ich 5 Münzen, ich werfe sie alle auf einmal und zähle, wie viele Köpfe ich bekomme. Oder ich könnte eine Münze haben, sie fünfmal werfen und zählen, wie oft ich „Kopf“ bekomme. Es spielt keine Rolle. Aber nehmen wir an, dass ich eine Münze habe und sie fünfmal werfen werde. Dann werden wir keine Unsicherheit haben. Hier ist also die Definition meiner Zufallsvariablen. Wie wir wissen, unterscheidet sich eine Zufallsvariable ein wenig von einer gewöhnlichen Variablen, sie ähnelt eher einer Funktion. Es gibt dem Experiment eine gewisse Bedeutung. Und diese Zufallsvariable ist ganz einfach. Wir zählen einfach, wie oft nach 5 Würfen „Kopf“ auftauchte – das ist unsere Zufallsvariable X. Lassen Sie uns darüber nachdenken, wie hoch die Wahrscheinlichkeiten verschiedener Werte in unserem Fall sein könnten. Wie groß ist also die Wahrscheinlichkeit, dass X (Großbuchstabe X) 0 ist? Diese. Wie groß ist die Wahrscheinlichkeit, dass es nach 5 Würfen keinen Kopf gibt? Nun, das ist im Wesentlichen dasselbe wie die Wahrscheinlichkeit, nur „Kopf“ zu bekommen (das ist richtig, ein kurzer Überblick über die Wahrscheinlichkeitstheorie). Sie sollten nur Schwänze bekommen. Wie groß ist die Wahrscheinlichkeit jedes dieser Köpfe? Das ist 1/2. Diese. Dies sollte 1/2 mal 1/2, 1/2, 1/2 und wieder 1/2 sein. Diese. (1/2)⁵. 1⁵=1, dividiere durch 2⁵, d.h. mit 32. Ganz logisch. Also... ich wiederhole ein wenig, was wir in der Wahrscheinlichkeitstheorie behandelt haben. Dies ist wichtig, um zu verstehen, wohin wir uns jetzt bewegen und wie tatsächlich die diskrete Wahrscheinlichkeitsverteilung entsteht. Wie hoch ist also die Wahrscheinlichkeit, dass wir genau einmal „Kopf“ bekommen? Nun, beim ersten Wurf könnte es Kopf geben. Diese. es könnte sein: „heads“, „tails“, „tails“, „tails“, „tails“. Oder es könnte beim zweiten Wurf „Kopf“ herauskommen. Diese. Es könnte eine Kombination wie diese geben: „tails“, „heads“, „tails“, „tails“, „tails“ und so weiter. Nach jedem der fünf Würfe könnte ein „Kopf“ erscheinen. Wie hoch ist die Wahrscheinlichkeit jeder dieser Situationen? Die Wahrscheinlichkeit, Kopf zu bekommen, beträgt 1/2. Dann wird die Wahrscheinlichkeit, Kopf zu bekommen, gleich 1/2, mit 1/2, mit 1/2, mit 1/2 multipliziert. Diese. Die Wahrscheinlichkeit jeder dieser Situationen beträgt 1/32. Dasselbe wie die Wahrscheinlichkeit einer Situation, in der X=0 ist. Im Wesentlichen beträgt die Wahrscheinlichkeit einer bestimmten Reihenfolge von Kopf und Zahl 1/32. Die Wahrscheinlichkeit dafür beträgt also 1/32. Und die Wahrscheinlichkeit dafür beträgt 1/32. Und solche Situationen treten auf, weil bei jedem der fünf Würfe „Kopf“ hätte fallen können. Daher beträgt die Wahrscheinlichkeit, dass genau ein „Kopf“ erscheint, 5*1/32, d.h. 5/32. Ganz logisch. Jetzt wird es interessant. Wie groß ist die Wahrscheinlichkeit ... (Ich schreibe jedes Beispiel in einer anderen Farbe) ... wie hoch ist die Wahrscheinlichkeit, dass meine Zufallsvariable gleich 2 ist? Diese. Ich werfe eine Münze fünfmal, und wie hoch ist die Wahrscheinlichkeit, dass sie genau zweimal „Kopf“ landet? Das ist interessanter, oder? Welche Kombinationen sind möglich? Es könnte Kopf, Kopf, Zahl, Zahl, Zahl sein. Es könnten auch „Kopf“, „Zahl“, „Kopf“, „Zahl“, „Zahl“ lauten. Und wenn Sie glauben, dass sich diese beiden „Adler“ in der Kombination an verschiedenen Stellen befinden können, können Sie etwas verwirrt sein. Es ist nicht mehr möglich, über Platzierungen so nachzudenken, wie wir es oben getan haben. Obwohl ... Sie können, aber Sie riskieren, verwirrt zu werden. Sie müssen eines verstehen. Für jede dieser Kombinationen beträgt die Wahrscheinlichkeit 1/32. ½*½*½*½*½. Diese. Die Wahrscheinlichkeit jeder dieser Kombinationen beträgt 1/32. Und wir sollten darüber nachdenken, wie viele solcher Kombinationen es gibt, die unsere Bedingung erfüllen (2 „Köpfe“)? Diese. Grundsätzlich müssen Sie sich vorstellen, dass eine Münze fünfmal geworfen wird und Sie zwei davon auswählen müssen, bei denen „Kopf“ erscheint. Stellen wir uns vor, dass unsere 5 Würfe in einem Kreis versammelt sind, und stellen wir uns auch vor, dass wir nur zwei Stühle haben. Und wir sagen: „Okay, wer von euch wird auf diesen Eagle-Stühlen sitzen? Diese. Wer von euch wird der „Adler“ sein? Und es interessiert uns nicht, in welcher Reihenfolge sie sich setzen. Ich gebe dieses Beispiel und hoffe, dass es Ihnen klarer wird. Und vielleicht möchten Sie sich einige Lektionen zur Wahrscheinlichkeitsrechnung zu diesem Thema ansehen, wenn ich über Newtons Binomial spreche. Denn dort werde ich noch ausführlicher auf all das eingehen. Aber wenn Sie so denken, werden Sie verstehen, was ein Binomialkoeffizient ist. Denn wenn Sie so denken: Okay, ich habe 5 Würfe, welcher Wurf wird zuerst „Kopf“ bringen? Nun, hier sind 5 Möglichkeiten, bei denen ein Wurf zum ersten Mal „Kopf“ ergibt. Wie viele Möglichkeiten gibt es für einen zweiten Adler? Nun ja, der erste Wurf, den wir bereits genutzt haben, hat eine Möglichkeit, Kopf zu bekommen, zunichte gemacht. Diese. Eine Kopfposition in der Kombination ist bereits durch einen der Würfe besetzt. Jetzt sind noch 4 Würfe übrig, was bedeutet, dass der zweite „Kopf“ auf einen der 4 Würfe fallen kann. Und Sie haben es gesehen, genau hier. Ich entschied mich dafür, dass es beim ersten Wurf „Kopf“ geben würde, und ging davon aus, dass einer der vier verbleibenden Würfe ebenfalls „Kopf“ ergeben würde. Hier gibt es also nur 4 Möglichkeiten. Ich sage nur, dass es für den ersten Kopf fünf verschiedene Positionen gibt, auf denen er landen kann. Und für den zweiten sind nur noch 4 Plätze frei. Denk darüber nach. Bei dieser Berechnung wird die Reihenfolge berücksichtigt. Aber für uns ist es jetzt egal, in welcher Reihenfolge „Kopf“ und „Zahl“ herausfallen. Wir sagen nicht, dass es Kopf 1 oder Kopf 2 ist. In beiden Fällen sind es nur Köpfe. Wir könnten vermuten, dass dies Heads 1 und dies Heads 2 ist. Oder es könnte umgekehrt sein: Dies könnte der zweite „Adler“ sein und dies könnte der „Erste“ sein. Und ich sage das, weil es wichtig ist zu verstehen, wo Platzierungen und Kombinationen verwendet werden. Uns geht es nicht um Konsistenz. Tatsächlich gibt es also nur zwei Möglichkeiten, wie unser Ereignis stattfinden kann. Also teilen wir dies durch 2. Und wie Sie später sehen werden, sind es 2! Entstehungswege unserer Veranstaltung. Wenn es drei Köpfe gäbe, dann wären es auch hier drei! Und ich zeige Ihnen, warum. Das ist also gleich ... 5*4=20 und dividiert durch 2 – Sie erhalten 10. Es gibt also 10 verschiedene Kombinationen von 32, in denen Sie definitiv 2 Köpfe haben werden. Also, 10*(1/32) entspricht 10/32, was bedeutet das? 5/16. Ich schreibe es in Form eines Binomialkoeffizienten. Das ist der Wert hier ganz oben. Wenn Sie darüber nachdenken, ist dies dasselbe wie 5!, geteilt durch ... Was bedeutet diese 5 * 4? 5! – das ist 5*4*3*2*1. Diese. Wenn ich hier nur 5*4 brauche, dann kann ich dafür 5 teilen! um 3! Dies entspricht 5*4*3*2*1 geteilt durch 3*2*1. Und es bleiben nur 5*4 übrig. Das ist also dasselbe wie dieser Zähler. Und dann, weil Die Reihenfolge interessiert uns nicht, wir brauchen hier 2. Eigentlich 2!. Mit 1/32 multiplizieren. Das wäre die Wahrscheinlichkeit, dass wir genau 2 Köpfe bekommen würden. Wie groß ist die Wahrscheinlichkeit, dass wir genau dreimal Kopf bekommen? Diese. die Wahrscheinlichkeit, dass X=3. Nach der gleichen Logik kann der erste Fall von „Kopf“ also bei einem von fünf Würfen auftreten. Der zweite Fall von „Kopf“ kann bei einem der vier verbleibenden Würfe auftreten. Und der dritte Fall von „Kopf“ kann bei einem von drei verbleibenden Würfen auftreten. Wie viele verschiedene Möglichkeiten gibt es, 3 Würfe anzuordnen? Wie viele Möglichkeiten gibt es im Allgemeinen, drei Objekte an ihren Platz zu bringen? Das sind 3! Und Sie können es herausfinden, oder Sie möchten vielleicht die Lektionen noch einmal durchgehen, in denen ich das ausführlicher erklärt habe. Wenn Sie aber zum Beispiel die Buchstaben A, B und C nehmen, dann gibt es insgesamt 6 Möglichkeiten, wie Sie diese anordnen können. Sie können sich diese als Fälle von Köpfen vorstellen. Hier könnte es ACB, CAB geben. Könnte BAC, BCA und ... sein. Was ist die letzte Option, die ich nicht erwähnt habe? CBA. Es gibt 6 Möglichkeiten, 3 verschiedene Objekte anzuordnen. Wir dividieren durch 6, weil wir diese 6 verschiedenen Arten nicht noch einmal zählen wollen, weil wir sie als gleich behandeln. Hier interessiert uns nicht, welcher Wurf Kopf ergibt. 5*4*3... Dies kann als 5!/2! umgeschrieben werden. Und dividiere es durch weitere 3!. Das ist er. 3! entspricht 3*2*1. Dreier werden geschnitten. Dies wird gleich 2. Dies wird gleich 1. Nochmals 5*2, d.h. entspricht 10. Jede Situation hat eine Wahrscheinlichkeit von 1/32, also entspricht dies wiederum 5/16. Und das ist interessant. Die Wahrscheinlichkeit, dass Sie 3 Köpfe bekommen, ist gleich der Wahrscheinlichkeit, dass Sie 2 Köpfe bekommen. Und der Grund dafür... Nun, es gibt viele Gründe, warum das passiert ist. Aber wenn Sie darüber nachdenken, ist die Wahrscheinlichkeit, drei Köpfe zu bekommen, genauso groß wie die Wahrscheinlichkeit, zwei Zahlen zu bekommen. Und die Wahrscheinlichkeit, drei Köpfe zu bekommen, sollte genauso groß sein wie die Wahrscheinlichkeit, zwei Köpfe zu bekommen. Und es ist gut, dass die Werte so funktionieren. Bußgeld. Wie groß ist die Wahrscheinlichkeit, dass X=4 ist? Wir können die gleiche Formel verwenden, die wir zuvor verwendet haben. Es könnte 5*4*3*2 sein. Hier schreiben wir also 5*4*3*2... Wie viele verschiedene Möglichkeiten gibt es, 4 Objekte anzuordnen? Das ist 4!. 4! – das ist tatsächlich dieser Teil, genau hier. Das ist 4*3*2*1. Dies wird also reduziert, so dass 5 übrig bleibt. Dann hat jede Kombination eine Wahrscheinlichkeit von 1/32. Diese. das entspricht 5/32. Und beachten Sie noch einmal, dass die Wahrscheinlichkeit, viermal „Kopf“ zu bekommen, gleich der Wahrscheinlichkeit ist, einmal „Kopf“ zu bekommen. Und das macht Sinn, denn... 4 Köpfe sind dasselbe wie 1 Schwanz zu bekommen. Sie sagen: Nun, bei welchem ​​Wurf wird dieses „Zahl“ auftauchen? Ja, dafür gibt es 5 verschiedene Kombinationen. Und jeder von ihnen hat eine Wahrscheinlichkeit von 1/32. Und schließlich: Wie groß ist die Wahrscheinlichkeit, dass X=5 ist? Diese. Köpfe erscheinen 5 Mal hintereinander. Es sollte so lauten: „Adler“, „Adler“, „Adler“, „Adler“, „Adler“. Jeder Kopf hat eine Wahrscheinlichkeit von 1/2. Sie multiplizieren sie und erhalten 1/32. Du kannst einen anderen Weg gehen. Wenn es 32 Möglichkeiten gibt, bei diesen Experimenten Kopf und Zahl zu erreichen, dann ist dies nur eine davon. Hier gab es 5 solcher Methoden von 32. Hier - 10 von 32. Dennoch haben wir die Berechnungen durchgeführt und sind nun bereit, die Wahrscheinlichkeitsverteilung zu zeichnen. Aber meine Zeit ist abgelaufen. Lassen Sie mich in der nächsten Lektion fortfahren. Und wenn Sie Lust haben, können Sie vielleicht zeichnen, bevor Sie sich die nächste Lektion ansehen? Bis bald!