Berechnung eines rekursiven digitalen Filters. Methoden der numerischen Integration. Methode der Impulsantwort-Invarianz. Forschungsarbeit „Methode der Invarianten“

Städtische Haushaltsbildungseinrichtung, Turnhalle Nr. 9

EXPERIMENTELL-ABSTRAKTES PROJEKT

Zu diesem Thema:

Anwendung der Methode der Invarianten bei der Lösung von Problemen des Einheitlichen Staatsexamens und der Olympiade

Durchgeführt:

Schüler XI Klasse „B“.

Tischchenko Elina

Wissenschaftlicher Leiter:

Mathematiklehrer

Khatuntseva

Irina Wladimirowna

Woronesch – 2017

Inhalt

Einführung

In der modernen Mathematik spielt der Begriff der Invarianz eine wichtige Rolle, d.h. Unveränderlichkeit eines mathematischen Objekts. Viele Definitionen der Mathematik beziehen sich tatsächlich auf dieses Konzept, obwohl der Begriff Invarianz selbst in Lehrbüchern fehlt.

Beispiel: Eine gerade Funktion f(x) mit Definitionsbereich R ist invariant, weil f(x)= f(-x).

Das Vorhandensein der einen oder anderen Invarianzeigenschaft in einem mathematischen Objekt ermöglicht es, einige allgemeine qualitative Eigenschaften dieses Objekts festzulegen.

Der Zweck dieser Arbeit besteht darin, die Verwendung der invarianten Methode zur Lösung von Problemen im Rahmen des Einheitlichen Staatsexamens und der Olympiade aufzuzeigen.

Eine Menge Literatur von führenden Universitäten des Landes, wie der Moskauer Staatsuniversität und dem Moskauer Institut für Physik und Technologie, widmet sich diesem Thema. Das klassische Buch zur Invariantentheorie ist das Buch des herausragenden deutschen Mathematikers Herlean Weyl. Und Studenten der Universität Oxford geben das jährliche Magazin „The Invariant“ heraus.

Dieses Thema scheint sehr relevant zu sein, denn... Die Methode der Invarianten ermöglicht es, Probleme mit erhöhtem Komplexitätsgrad ganz einfach zu lösen.

Kapitel 1. Anwendung der Invarianto-Methode bei der Lösung von Olympia-Problemen

Parität (ungerade Parität), Divisionsrest, Permutation, Färbung usw. werden am häufigsten als Invarianten betrachtet.

Die Verwendung von Parität ist eine der am häufigsten vorkommenden Ideen bei der Lösung von Olympiadenproblemen. Formulieren wir die wichtigsten Aussagen, die der Anwendung dieser Idee zugrunde liegen:

die Parität der Summe mehrerer ganzer Zahlen stimmt mit der Parität der Anzahl ungerader Terme überein;

Das Vorzeichen des Produkts mehrerer (ungleich Null) Zahlen wird durch die Gleichmäßigkeit der Anzahl negativer Faktoren bestimmt.

Aufgabe 1.

An der Tafel stehen zehn Vor- und fünfzehn Nachteile. Es ist erlaubt, zwei beliebige Zeichen zu löschen und stattdessen ein Pluszeichen zu schreiben, wenn sie gleich sind, andernfalls ein Minuszeichen. Welches Zeichen bleibt auf der Tafel, nachdem vierundzwanzig solcher Operationen durchgeführt wurden?

Lösung.

Ersetzen Sie jedes Pluszeichen durch eine Zahl1 , und jedes Minus ist eine Zahl-1 .

Dann löschen wir zwei beliebige Zahlen und notieren ihr Produkt. Daher bleibt das Produkt aller an der Tafel geschriebenen Zahlen unverändert.

Da das Produkt zunächst negativ war (15 negative Zahlen), bleibt es am Ende bestehenNegativ.

Antwort: Minus.

Aufgabe 2.

Der Junge bekam in seinem Mathetest eine schlechte Note und riss in einem Anfall von Verzweiflung den Zettel mit seiner Arbeit in zehn Stücke. Dann riss er eines der entstandenen Stücke in 10 weitere Stücke. Kann es am Ende der Entspannung 2015 Zettel geben?

Lösung.

Jedes Mal, wenn er ein Stück Papier um 10 zerreißt, erhöht der Junge die Gesamtzahl der Papierstücke um 9. Nach dem ersten Zerreißen hat er 1+9=10 Stücke, nach dem zweiten - 10+9=19 Stücke usw . Das heißt, die Anzahl der Papierstücke beim n-ten Riss wird durch die Formel 1+9 bestimmtN.

Prüfen wir, ob die Zahl 2015 als 1+9 darstellbar istN:

1+9 N=2015;

9 N=2014.

Das Jahr 2014 ist nicht ohne Rest durch 9 teilbar, daher kann es am Ende der Lockerung keine 2015-Teile geben.

Antwort: Nein

Aufgabe 3.

Die Tafel enthält Zahlen von 1 bis 1998. Sie dürfen zwei beliebige Zahlen in einem Zug löschen und stattdessen deren Differenz aufschreiben, bis nur noch eine Zahl übrig ist. Könnte diese Zahl Null sein?

Lösung.

Betrachten Sie die Summe aller Zahlen, die vor und nach einem Schritt an die Tafel geschrieben wurden. Mögen wir die Zahlen löschenA, B. Dann war zuerst die Summe aller Zahlen gleich und dann woS– die Summe aller anderen Zahlen. Wie wir sehen können, ist der Ersatz (A+ B) An (A- B) ändert nichts an der Parität der Summe aller Zahlen. Die Summe der Zahlen ganz am Anfang ist eine ungerade Zahl (
), was bedeutet, dass bei jedem Schritt die Summe der an die Tafel geschriebenen Zahlen ungerade ist. Null ist eine gerade Zahl, daher können wir sie nicht auf die Tafel bringen.

Antwort: Nein.

Aufgabe 4.

Jede Zelle einer quadratischen 2*2-Tabelle ist schwarz oder weiß gefärbt, wie in der Abbildung unten dargestellt. Mit einem Zug können Sie Zellen in jeder Zeile, in jeder Spalte oder in jeder Diagonale neu einfärben: schwarze zu weiß und weiße zu schwarz. Ist es möglich, in wenigen Zügen eine Tabelle zu erhalten, bei der alle Zellen weiß sind?

Lösung.

Weisen wir jeder Zelle 1 zu, wenn sie weiß gestrichen ist, und -1, wenn sie schwarz gestrichen ist. Dann bedeutet der Wechsel der Farben einen Wechsel der Zeichen. Betrachten Sie das Produkt aller Zahlen, die den Zellen entsprechen. Da wir beim Umfärben die Vorzeichen von genau zwei Faktoren ändern, ändert sich das Produkt aller vier Zahlen nicht. Ganz am Anfang ist dieses Produkt gleich -1. Die erforderliche Einfärbung entspricht einem Produkt gleich 1. Daher ist es nicht möglich, die Tabelle mit den angegebenen Operationen neu einzufärben.

Antwort: Nein.

Aufgabe 5.

Drei Stapel enthalten 1, 9 und 98 Steine. In einem Zug dürfen Sie einen Stein von zwei beliebigen Stapeln nehmen und auf den dritten legen. Ist es möglich, in wenigen Zügen alle Steine ​​in einem der Stapel einzusammeln?

Lösung.

Betrachten wir die Reste, wenn wir die ursprünglichen Zahlen durch drei dividieren – die Anzahl der Steine ​​in Stapeln. Im ersten Stapel ist der Rest 1, im zweiten - 0, im dritten - 2. Betrachten wir, was aus der Sicht der Reste als nächstes passieren wird, wenn wir die Steine ​​verschieben:

Wir haben eine Invariante gefunden – nach jeder Operation sind die Reste gleich: 0, 1, 2, nur werden sie unterschiedlich verteilt. Wenn wir alle Steine ​​auf einem Stapel sammeln können, sind die Reste bei Division durch 3 in allen Stapeln gleich (gleich 0). Folglich ist es mit den angegebenen Vorgängen unmöglich, alle Steine ​​auf einem Stapel zu sammeln.

Antwort: Nein.

Aufgabe 6.

Auf der Ebene wird eine sich nicht selbst schneidende geschlossene gestrichelte Linie angegeben, deren drei Eckpunkte nicht auf derselben Geraden liegen. Nennen wir ein Paar nicht benachbarter Links eine Polyliniebesonders, wenn die Fortsetzung eines von ihnen die andere schneidet. Beweisen Sie, dass die Anzahl der speziellen Paare gerade ist.

Lösung.

Nehmen wir die benachbarten Verbindungen AB und BC und nennen sie sieEcke ein Winkel symmetrisch zum Winkel ABC relativ zum Punkt B (in der Abbildung unten ist die Ecke schattiert). Für alle Eckpunkte der gestrichelten Linie können die gleichen Ecken berücksichtigt werden. Es ist klar, dass die Anzahl der Sonderpaare gleich der Anzahl der Schnittpunkte der Verbindungen mit den Ecken ist. Es bleibt zu beachten, dass die Anzahl der Segmente der gestrichelten Linie, die eine Ecke schneiden, gerade ist, da Auf dem Weg von A nach C tritt die gestrichelte Linie so oft in die Ecke ein, wie sie sie verlässt (dies ergibt sich aus der Bedingung, dass keine drei Eckpunkte der gestrichelten Linie auf derselben Geraden liegen). Daher ist die Anzahl der speziellen Paare gerade, was wir beweisen mussten.

Aufgabe 7 (Regionalphase der Allrussischen Olympiade für Schüler, 2016-2017, 11. Klasse, zweiter Tag, Nr. 8).

Zunächst werden 100 Karten auf den Tisch gelegt, auf denen jeweils eine natürliche Zahl steht; Darüber hinaus befinden sich darunter genau 28 Karten mit ungeraden Zahlen. Dann wird jede Minute der nächste Vorgang durchgeführt. Für jeweils 12 auf dem Tisch liegende Karten wird das Produkt der darauf geschriebenen Zahlen berechnet, alle diese Produkte addiert und die resultierende Zahl auf eine neue Karte geschrieben, die zu den auf dem Tisch liegenden Karten hinzugefügt wird. Ist es möglich, die ersten 100 Zahlen so zu wählen, dass für jedes natürliche d früher oder später eine Karte mit einer durch teilbaren Zahl entsteht?
?

Lösung.

Wenn unter den Zahlen auf den Karten irgendwann genau k ungerade Zahlen sind, dann sind es unter den Produkten der Zahlen genau 12
seltsam; Daher wird die Zahl auf der nächsten hinzugefügten Karte genau dann ungerade sein, wenn sie ungerade ist (und dann erhöht sich k in dieser Minute um 1).

Es ist leicht zu erkennen, dass die Zahl
ungerade (dies folgt aus der Tatsache, dass die Zweierpotenzen enthalten sind
Und
, sind gleich). Bei der sequentiellen Überprüfung stellen wir außerdem fest, dass das erste
,
,
- ungerade Zahlen und
- sogar. Wenn also die Anzahl der ungeraden Karten 32 erreicht, erhöht sie sich nicht mehr und es liegen immer nur noch 32 ungerade Karten auf dem Tisch und alle addierten Zahlen sind gerade.

Lass es jetzt N-nächster Schritt – die Summe aller Produkte von 12 aus den auf den Karten geschriebenen Zahlen und – die Summe aller Produkte von 11 Zahlen. Nummer
, das auf der nächsten Karte geschrieben wird, unterscheidet sich von für die Summe der Produkte von 12 Zahlen, unter denen gerade eine gerade Zahl hinzugefügt wurde , d.h. An
. Bedeutet, . Nummer - gerade, da die Anzahl der ungeraden Summen 11 beträgt
sogar. Bedeutet,
ungerade und die maximale Potenz von zwei, die durch teilbar ist
gleich der maximalen Potenz von zwei, die durch teilbar ist . Das bedeutet, dass anfangs keine Zahlen auf dem Tisch lagen, was für jeden natürlich wäreDdurch dividiert wurden, werden solche Zahlen nicht weiter angezeigt.

Antwort: Nein, das geht nicht.

Kapitel 2. Anwendung der Invariantenmethode bei Unified State Examination-Problemen, die einen Parameter enthalten

Nach der Analyse einer Vielzahl von Problemen wurde ein Algorithmus zur Lösung von Problemen mit einem Parameter mithilfe der Invariantenmethode erstellt.

Algorithmus zur Lösung von Problemen mit Parametern unter Verwendung einer Invariante:

1) eine gegebene Gleichung, Ungleichung, ein gegebenes Gleichungssystem (Ungleichungen) auf Invarianz prüfen;

2) Finden Sie akzeptable Werte des Parameters, indem Sie prüfen, ob die Bedingungen erfüllt sind: Wenn „Symmetrie in Bezug auf das Vorzeichen der Variablen“ vorliegt, ersetzen Sie ihren Nullwert; mit „Symmetrie in Bezug auf die Permutation von Variablen“ werden alle Variablen mit einem Buchstaben bezeichnet;

3) Überprüfen Sie, ob die gefundenen Parameterwerte die Bedingungen des Problems erfüllen.

4) Schreiben Sie die Antwort auf.

Aussage 1 . Wenn der Ausdruck
invariant unter Transformation
und Gleichung
hat eine Wurzel ,Das

Aussage 2. Wenn der Ausdruck

und Gleichung
hat eine Lösung
, dann ein Zahlenpaar

Aussage 3 . Wenn der Ausdruck
Transformationsinvariante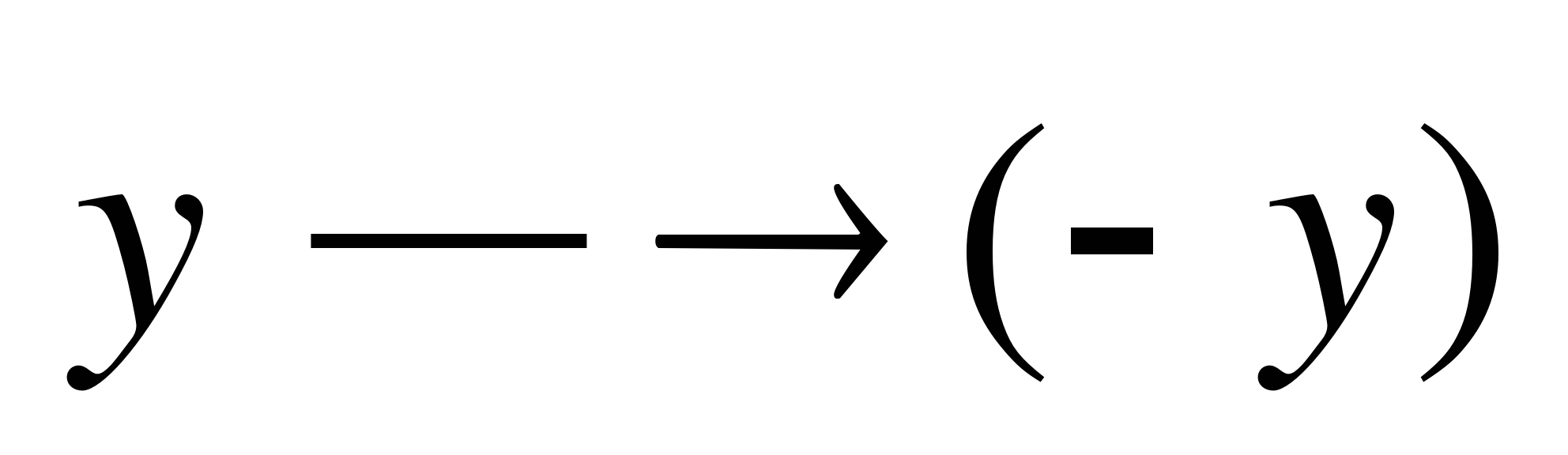
und Gleichung
hat eine Lösung
, dann ein Zahlenpaar
auch die Lösung dieser Gleichung.

Aussage 4. Wenn der Ausdruck
Transformationsinvariante
Und
, und die Gleichung
hat eine Lösung
, dann ein paar Zahlen
auch die Lösung dieser Gleichung.

Aussage 5. Wenn der Ausdruck
Transformationsinvariante
, Die gleichung
hat eine Wurzel , Das
auch die Wurzel dieser Gleichung.

Aufgabe 1.

Finden Sie alle Werte des Parameters a, für die die Gleichung eine Lösung hat

Lösung.

Beachten Sie, dass wenn ist die Wurzel der Gleichung, dann - - auch eine Wurzel => es kann nur eine Wurzel geben, wenn =-=0.
Lasst uns ersetzen
:

Bei
:

1 Wurzel, geeignet

Bei
:

Die linke Seite dieser Gleichung ist größer oder gleich
, und diese untere Grenze ist genau – sie wird bei erreicht
. Die Schätzung der rechten Seite ist etwas schwieriger. Beachten Sie dies zunächst beim Ändern einer Variablen aus
Vor
Ausdruck
ändert sich von -1 auf 1. Auf dem Segment
Funktion
steigt monoton ab
Vor
. Daher der Ausdruck
variiert zwischen
Vor
. Dementsprechend variiert die rechte Seite von Gleichung (1).
Vor
, und die Werte der rechten Seite der Gleichung füllen dieses Segment vollständig aus. Aus den gewonnenen Informationen über die möglichen Werte der linken und rechten Seite der Gleichung (1) folgt, dass sie nur dann gleich sein können, wenn sie gleichzeitig gleich sind
. Mit anderen Worten, Gleichung (1) entspricht dem System:

Die erste Gleichung hat eine einzige Wurzel
, was auch die zweite Gleichung des Systems erfüllt. Das bedeutet, dass das System und damit auch die ursprüngliche Gleichung eine eindeutige Lösung hat
. Daher wird der Parameterwert überprüft (
) muss in der Aufgabenantwort enthalten sein.

Antwort: 0;
.

Aufgabe 2. System der Ungleichheiten
hat eine einzige Lösung?

Lösung. 1. In diesem System beobachten wir „Symmetrie unter Änderung von Variablen“. Dann, wenn es eine Lösung für das System gibt, dann
auch die Lösung des Systems. Die Einzigartigkeit der Lösung wird unter der Bedingung erreicht
(Aussage 4).

2. Alle Variablen bezeichnen durch
Aus einer Ungleichung, die eine eindeutige Lösung hat, wenn die Diskriminante eines quadratischen Trinoms Null ist, diese.

3. Überprüfen wir, ob das System eine eindeutige Lösung für die gefundenen Parameterwerte hat.

a) Setzen wir in dieses Ungleichungssystem ein
:

Addieren wir die Ungleichungen des letzten Systems:
+

Wenn wir die Klammern öffnen und ähnliche Begriffe hinzufügen, erhalten wir: . Von hier



- einzige Entscheidung.

b) Bei Auswechslung
Wir bekommen die einzige Lösung

Antwort:

Aufgabe 3. Finden Sie alle Werte des Parameters, für den das Gleichungssystem gilt

hat vier verschiedene Lösungen.

Lösung.

Aus der Form des Systems folgt, dass > 0.

1. Das System ist invariant, wenn es durch - und ersetzt wird An - . Deshalb, wenn der gewünschte Wert des Parameters und ein Zahlenpaar ;
- Lösung des Systems, dann Paare
;
, ;
Und
; -
auch Systemlösungen. (Aussagen 2 und 3). Deshalb finden wir Lösungen für ≥ 0, ≥0. Lassen Sie uns die Graphen der Gleichungen in einem Koordinatensystem darstellen. Diagramm der ersten Gleichung – Punkte der Seiten des QuadratsA B C D, der Graph des zweiten ist ein Kreis mit einem Mittelpunkt im Ursprung und einem Radius gleich .

Die Abbildung zeigt, dass das System in zwei Fällen genau vier Lösungen hat: 1)


;
; als > 0 also
; 2) = 0 E- der Radius eines Kreises, der in ein Quadrat eingeschrieben ist, dessen Seite gleich ist
nach Pythagoras aus dem Dreieck BOS.

Bedeutet, 0E =
, dann =
Wo 2
= 2; 2 =
und =
.

Antwort: = 1; =
.

Aufgabe 4. Bei welchen Parameterwerten Gleichungssystem
hat genau drei Lösungen?

Lösung. 1. Wenn ein Zahlenpaar ;
– Lösung des Systems, - der gewünschte Parameter, dann das Paar

; -
– auch eine Lösung des Systems. Bedeutet, = -
= 0.(Aussage 3).

2. Lassen Sie uns ersetzen = 0 in dieses Gleichungssystem ein.

Wir bekommen:

Überprüfen wir, ob diese Gleichung mit den gefundenen Werten zutrifft einzige Entscheidung. Bei =-3 wir haben:

Lösen wir die zweite Gleichung des Systems:

oder
hat keine Lösungen.

Wenn y=0, dann ist x=5 und (-5; 0) ist die einzige Lösung für das System. Bedeutet,
ungeeignet.. Abschluss

Im Rahmen der geleisteten Arbeit wurde die Methode der Invarianten untersucht. Die Methode der Invarianten wurde verwendet, um Probleme des Einheitlichen Staatsexamens, die einen Parameter enthielten, und Olympiade-Probleme zu Färbung, Parität und Divisionsresten zu lösen. Die praktische Anwendung der Methode wurde begründet und klar gezeigt.

Liste der verwendeten Literatur

Bei der Synthese eines diskreten Filters mithilfe eines analogen Prototyps ist es erforderlich, die Übertragungsfunktion des analogen Filters zu transformieren H(s) zur diskreten Filterübertragungsfunktion H(z). Der resultierende diskrete Filter kann in seinen Eigenschaften nicht vollständig mit dem analogen identisch sein – schon allein deshalb, weil die Frequenzeigenschaften des diskreten Filters periodisch sind. Man kann nur über bestimmte Dinge reden Einhaltung Eigenschaften von analogen und diskreten Filtern. Da die Theorie der Approximation idealer Frequenzantworten mit analogen Mitteln gut entwickelt ist, haben sich Methoden zur Synthese diskreter Filter mithilfe analoger Prototypen weit verbreitet.

In diesem Abschnitt betrachten wir zwei Methoden zur Synthese rekursiver diskreter Filter mithilfe analoger Prototypen:

Methode der invarianten Impulsantworten.

Diese einfachste Methode der digitalen Filtersynthese basiert auf der Annahme, dass der synthetisierte digitale Filter eine Impulsantwort haben muss, die das Ergebnis der Abtastung der Impulsantwort des entsprechenden Prototyp-Analogfilters ist.

Die Methode der invarianten IR-Transformation beinhaltet die Berechnung eines diskreten Filters, dessen IR ein diskretisierter IR des Prototypfilters ist. Die Diskretisierung einer Zeitfunktion führt bekanntlich dazu, dass das Spektrum der Funktion periodisch wird mit einer Periode gleich der Abtastfrequenz. Beim Übergang vom kontinuierlichen IR zum diskreten IR beginnt sich daher der Frequenzgang des Filters periodisch mit einer Verschiebung gleich der Abtastfrequenz zu wiederholen f 2. Wenn die Frequenz f 2 Wird im Vergleich zu den charakteristischen Frequenzgangfrequenzen des Prototypfilters recht hoch eingestellt, dann entspricht der diskrete Filter in seinen Eigenschaften dem kontinuierlichen Prototypfilter.

Unter Berücksichtigung der Synthese physikalisch realisierbarer Systeme, bei denen die Impulsantwort bei t verschwindet< 0, получим следующее выражение импульсной характеристики ЦФ:

(h k )=(h(0), h(Δ), h(2Δ)) (*)

Es ist zu beachten, dass die Anzahl der einzelnen Terme im Ausdruck der Impulsantwort des digitalen Filters entweder endlich oder unendlich sein kann. Dies bestimmt die Struktur des synthetisierten Filters: Ein Transversalfilter entspricht einer Impulsantwort mit einer endlichen Anzahl von Abtastwerten, während ein rekursiver digitaler Filter erforderlich ist, um eine unendlich ausgedehnte Impulsantwort zu implementieren.

Der Frequenzgang des resultierenden Filters steht in gleicher Beziehung zum Frequenzgang des analogen Prototyps wie das Spektrum des abgetasteten Signals zum Spektrum des analogen Signals – periodische Wiederholung. Um mit dieser Synthesemethode gute Ergebnisse zu erzielen, muss daher der Gewinn des analogen Prototyps bei Frequenzen oberhalb der Nyquist-Frequenz vernachlässigbar sein. Daraus folgt auch, dass diese Methode zum Erstellen von Tiefpassfiltern und Bandpassfiltern geeignet ist, jedoch nicht zum Synthetisieren von Hochpassfiltern und Notchfiltern.

Als Beispiel synthetisieren wir einen Tschebyscheff-Tiefpassfilter 2. Ordnung mit einer Grenzfrequenz von 10 kHz unter Verwendung der Methode der invarianten Impulsantwort und wählen gezielt eine Abtastfrequenz, die nicht hoch genug ist (48 kHz), um das klar zu erkennen Effekte im Zusammenhang mit der Überlagerung verschobener Kopien des Spektrums (Abb. 6.2):

Reis. 6.2. Frequenzgang eines analogen Prototyps (gestrichelte Linie) und eines diskreten Filters (durchgezogene Linie), synthetisiert mit der Methode der invarianten Impulsantwort

Die Abbildung zeigt deutlich, dass aufgrund der nicht ausreichend hohen Abtastfrequenz der Transmissionskoeffizient des analogen Filters bei der Nyquist-Frequenz nicht ausreichend klein ist, was zu merklichen Verzerrungen in der Form des Frequenzgangs des synthetisierten diskreten Filters führt. Durch Erhöhen der Abtastrate werden diese Verzerrungen vernachlässigbar.

Der Grad der Annäherung der Amplituden-Frequenz-Charakteristik des synthetisierten digitalen Filters an die Charakteristik des analogen Prototyps hängt vom gewählten Abtastschritt ab Δ . Bei Bedarf sollten Sie den Frequenzübertragungskoeffizienten des digitalen Filters berechnen, indem Sie die Variable in der Systemfunktion H(z) mithilfe der Formel ersetzen z=exp(jωΔ), und vergleichen Sie dann das Ergebnis mit der Frequenzverstärkung der analogen Schaltung.

Beispiel

Betrachten Sie die Synthese eines transversalen digitalen Filters ähnlich einem dynamischen System 1. Ordnung (z. B. einer integrierenden RC-Schaltung) mit einer Impulsantwort der Form

(Der für das Syntheseproblem unwichtige Amplitudenmultiplikator in der Impulsantwort wird gleich Eins gesetzt).

Die Impulsantwort soll durch eine Folge von drei gleichabständigen Abtastwerten angenähert werden:

Ein transversales digitales Filter mit einer solchen Impulsantwort wird durch die Differenzengleichung beschrieben

Anwenden einer Z-Transformation auf die Sequenz , finden wir die Systemfunktion CF

Woher kommt der Frequenzübertragungskoeffizient?

Beispiel

Betrachten Sie den Fall, dass die Impulsantwort einer analogen Schaltung durch eine unendliche diskrete Folge angenähert wird

()

Nachdem wir die Z-Transformation der Impulsantwort () durchgeführt haben, erhalten wir die Systemfunktion

()

Diese Systemfunktion entspricht einem rekursiven digitalen Filter 1. Ordnung, der neben dem Addierer einen Skalenblock und ein Verzögerungselement enthält.

Frequenzverstärkung des Filters

Methode der invarianten Frequenzcharakteristik (bilineare Transformation).

Es ist grundsätzlich unmöglich, einen digitalen Filter zu erstellen, dessen Frequenzgang genau den Frequenzgang einer analogen Schaltung nachbildet. Der Grund dafür ist, dass der Frequenzübertragungskoeffizient eines digitalen Filters bekanntlich eine periodische Funktion der Frequenz ist, wobei die Periode durch den Abtastschritt bestimmt wird (Abb.).

Reis. . Amplituden-Frequenz-Eigenschaften von Filtern:

a - analog; 6 - digital

Wenn wir über die Ähnlichkeit (Invarianz) der Frequenzeigenschaften analoger und digitaler Filter sprechen, können wir nur verlangen, dass der gesamte unendliche Frequenzbereich gilt ω ein, bezogen auf das analoge System, wurde in ein Frequenzsegment umgewandelt ω c Digitalfilter, der die Ungleichung erfüllt

-π/Δ<ω ц < π/Δ

unter Beibehaltung des allgemeinen Erscheinungsbildes des Frequenzgangs.

Sei K a (p) die Übertragungsfunktion des analogen Filters, gegeben durch einen gebrochenrationalen Ausdruck in Potenzen der komplexen Frequenz R . Wenn wir die Beziehung zwischen den Variablen z und p verwenden:

z = exp(pΔ),

dann können wir schreiben

p = (1/ Δ) ln z (hh)

Allerdings ist es mit diesem Verbindungsgesetz unmöglich, eine physikalisch realisierbare Systemfunktion CF zu erhalten, da die Substitution (hch) in den Ausdruck Ks(p) zu einer Systemfunktion führt, die nicht als Quotient zweier Polynome ausgedrückt wird. Es ist erforderlich, eine gebrochenrationale Funktion von z zu finden, die die grundlegende Transformationseigenschaft (tch) hätte, nämlich Punkte des Einheitskreises, die in der z-Ebene liegen, auf Punkte der imaginären Achse auf der p-Ebene übertragen würde.

Unter anderen Methoden zur Synthese von Tiefpassfiltern hat sich eine Beziehung der Form weit verbreitet

Herstellen einer Eins-zu-eins-Entsprechung zwischen den Punkten des Einheitskreises in der z-Ebene und der gesamten imaginären Achse in der p-Ebene. Ein charakteristisches Merkmal dieses Transformationsgesetzes ist wie folgt. Die Änderung der Variablen soll in (15.97) erfolgen.

z = exp(j ω Δ),.

Daraus folgt die Beziehung zwischen den Frequenzvariablen des COA und sozialen analogen und digitalen Systemen:

(15.98)

Wenn die Abtastrate hoch genug ist ( ω c Δ <<1), то, как легко видеть из формулы (15.98), . Таким образом, на низких частотах характеристики аналогового и цифрового фильтров практически совпадают. В общем случае нужно принимать во внимание трансформацию масштаба по оси частот цифрового фильтра, описываемого формулой (15.98).

In der Praxis besteht das Verfahren zur Synthese digitaler Filter darin, die Variable in der Funktion Kl(p) der Analogschaltung gemäß Formel (15.97) zu ersetzen. Die resultierende Systemfunktion DF erweist sich als gebrochenrational und ermöglicht daher das direkte Schreiben des digitalen Filteralgorithmus.

Beispiel

Synthetisieren Sie einen digitalen Filter mit einem Frequenzgang, der dem eines analogen Tiefpassfilters ähnelt. Grenzfrequenz für Digitalfilter ω sc = 1500 s -1. Abtastfrequenz ω d = 10000 s -1.

Zunächst legen wir den Sampling-Schritt fest

Um einen diskreten Filter mit bestimmten Grenzfrequenzen zu erhalten, müssen die Grenzfrequenzen des analogen Prototyps angepasst werden, um Verzerrungen der Frequenzachse zu kompensieren. Um also einen diskreten Tiefpassfilter mit einer Grenzfrequenz ceod zu synthetisieren, muss der Prototyp des analogen Filters eine Grenzfrequenz 00 a haben, die wie folgt mit 0 d verknüpft ist:

Mit der Formel (15.98) ermitteln wir die Grenzfrequenz eines analogen Filters ähnlich dem synthetisierten digitalen Filter:

Übertragungsfunktion des analogen Tiefpassfilters

K a (r)

Durch Ersetzen einer Variablen der Form (15.97) finden wir die Systemfunktion der digitalen Funktion:

Reis. 60. Amplituden-Frequenz-Eigenschaften des Prototypfilters (1) und der synthetisierten IIR-Filter (2-5)

Beim Vergleich der Kurven 1 und 2 sehen wir, dass Aliasing, das für einen diskreten Filter (Invar Met) charakteristisch ist, zu einer Verschlechterung des Frequenzgangs des Filters im Vergleich zum Prototypfilter führt. Diese Verschlechterung fällt jedoch umso geringer aus, je höher das Abtastratenverhältnis ist f 2 =1/T 2 zur Filter-Grenzfrequenz f c. IN in diesem Fall f 2 /fс=10. Wenn Sie zum Beispiel wählen f 2 /f c =20, dann erhalten wir für ein diskretes Filter den durch Kurve 3 in Abb. dargestellten Frequenzgang. 60. Diese Kurve liegt merklich näher an Kurve 1 (Frequenzgang des Prototypfilters) als an Kurve 2.

Aus einem Vergleich des Frequenzgangs eines diskreten IIR-Filters, der mit der Methode der invarianten IM-Transformation berechnet wurde (Kurven 2 und 3 in Abb. 60) und des IIR-Filters, der mit der Methode der bilinearen Transformation ermittelt wurde (Kurve 4), wird deutlich, dass der zweite Die Methode liefert niedrigere Werte des Frequenzgangs im Sperrbereich. Dies wird durch das Fehlen des für die invariante IR-Transformationsmethode charakteristischen Aliasing-Effekts erklärt.

Gleichzeitig ist ein Vergleich der Kurven 1 und 4 in Abb. 60 gibt Anlass zu der Schlussfolgerung, dass die bilineare Transformationsmethode zu einer gewissen Änderung der Skala entlang der Frequenzachse führt: Bei einem diskreten Filter tritt der Frequenzgangsabfall früher auf als bei einem kontinuierlichen Prototypfilter. Zusammenhang zwischen Häufigkeit F kontinuierlicher Filter und Frequenz fn Diskreter Filter kann aus Gleichheit gefunden werden (330)

Die Methode der Transformation der invarianten Impulsantwort behält also den Maßstab des Frequenzgangdiagramms entlang der horizontalen Achse (Frequenzachse) bei, erzeugt jedoch aufgrund des Aliasing-Effekts Verzerrungen entlang der vertikalen Achse. Bei der bilinearen Transformationsmethode ist das Bild umgekehrt: Der Graph wird nicht entlang der vertikalen Achse verzerrt, aber der Graph wird auf der horizontalen Achse verformt. Wenn man die Art dieser Verformung kennt, ist es möglich, im Voraus entsprechende Änderungen am Frequenzgang des Prototypfilters vorzunehmen, um das gewünschte Ergebnis zu erzielen.

Die schleifeninvariante Methode ist ein Sonderfall der Iterationsmethode.

Eine bestimmte Menge von Werten M wird angegeben, P M ist eine Teilmenge der Ergebnisse. Wir müssen den Punkt x  P finden. Dazu wählen wir die Mengen I M und Q M aus, so dass   I  Q  P. Unsere Aufgabe besteht also darin, den Punkt zu finden, der zu gehört Schnittpunkt dieser Mengen. Darüber hinaus werden wir nur solche Transformationen verwenden, die I nicht verlassen, d. h. in unserem Fall ist die Zugehörigkeit eines Punktes zur Menge I eine Invariante (ein konstanter Wert).

Sei x0  I der Ausgangspunkt.

Т:I\QI – die Transformation ist invariant in Bezug auf die Zugehörigkeit des Punktes zur Menge I.

Illustration für das Obige:

Unter der Wirkung der Transformation T geht Punkt x0 zu einem Punkt x1, der zur Menge I gehört. Punkt x1 geht wiederum zu Punkt x2, der ebenfalls zu I gehört. Dieser Prozess wird fortgesetzt, bis ein Punkt xN zu einem Punkt geht, der zu I gehört zu einer Menge Q, die so gewählt ist, dass ihr Schnittpunkt mit I in P enthalten ist. Der resultierende Punkt gehört auf der einen Seite zu Q und auf der anderen Seite zu I, aufgrund der Invarianz der Transformation T in Bezug auf I.

Programmschema:

während nicht q(x) tun

(x  IQ  P)

Schreiben wir ein Programm, das die oben beschriebene Methode veranschaulicht und sicherstellt, dass eine Zahl auf eine positive ganze Zahl potenziert wird.

Type_Real = single;

Funktion power(x: _Real; n: _Unsign ): Real;

(x ist die Basis, n ist der Exponent. Die Unterroutine sorgt für Potenzierung)

while n > 0 do (z*x n - invariant)

if odd(n) then (ungerade Paritätsprüfung)

dec(n); (n:=n-1)

n:= n chr 1; (n:= n div 2)

Lassen Sie uns beweisen, dass dieses Programm in einer endlichen Anzahl von Schritten abgeschlossen werden kann. Das Unterprogramm beendet seine Arbeit, wenn z = x n, d.h. dient dazu, x in die n-te Potenz zu erhöhen. Die Anzahl der Wiederholungen ist gleich der Anzahl „0“ + 2*der Anzahl „1“ –1 in der binären Schreibweise der Zahl n<= 2*количество значащих цифр – 1 в двоичной записи = 2*]log 2 n[ - 1. При этом данная программа будет очень эффективна.

Invariante Funktionsmethode.

Die Methode der invarianten Funktion ist ein Sonderfall der Methode der Schleifeninvariante.

In diesem Fall ist x = x0 und es ist notwendig, f(x0) zu berechnen. Dabei

I = (set x | f(x) = f(x0))

P = (die Menge x | f(x) ist leicht zu berechnen).

Konstruieren wir eine Transformation T – invariant bezüglich I, und nehmen wir den Wert P selbst (Q = P) als Abbruchbedingung.

Programmschema:

x:= x0; (x  I)

während p(x) dies nicht tut

begin (x  I\P)

x:= T(x); (x  I)

Ende; (x  P  I)

Um die Korrektheit zu beweisen, reicht es zu beweisen, dass die Schleife in einer endlichen Anzahl von Schritten ausgeführt wird.

Schreiben wir ein Programm, das diese Methode veranschaulicht.

Sei x = (a, b) und f(x) = N.O.D.(a, b). Es ist notwendig, N.O.D.(a, b) zu berechnen.

Dieses Programm nutzt die Tatsache, dass der Teiler zweier Zahlen ist

wird ein Teiler ihrer Differenz sein.

a:= a0; b:= b0; (>=0)

während (a>0) und (b>0) dies tun

Wenn a>b, dann a:= a - b

sonst b:= b – a;

Ergebnis:= a+b; (Die Bedingung für das Verlassen der Schleife ist die Gleichheit von entweder a oder b mit 0. Die Summe dieser Zahlen ergibt also die Zahl, die ungleich 0 ist.)

Das Verfahren zum Übergang von analogen Filtern zu digitalen Filtern wird als Impulsantwort-Invarianzmethode bezeichnet.

Reis. 12.9. Berechnungsverfahren unter Verwendung der Impulsantwort-Invarianzmethode. (siehe Scan)

Dieses Verfahren stellt fest, dass die Impulsantwort des resultierenden digitalen Filters ein Beispiel der Impulsantwort des entsprechenden analogen Filters ist und wird wie folgt bestimmt:

wobei T das Abtastintervall ist. Das Entwurfsverfahren mit dieser Methode ist in Abb. dargestellt. 12.9.

Zur Veranschaulichung der Impulsantwort-Invarianzmethode

Zerlegen wir die Übertragungsfunktion des ursprünglichen analogen Filters in einfache Brüche

wobei wir davon ausgehen, dass alle Pole unterschiedlich sind. Darüber hinaus stellt jedes den Pol des Analogfilters dar und stellt die Subtraktion der Funktion am Pol dar. Die Impulsantwort des Analogfilters kann durch Ausführen der inversen Laplace-Transformation von Gleichung (12.29) erhalten werden, die ergibt

Wo ist eine Einheitsschrittfolge? Durch Einsetzen des Ausdrucks (12.30) in die Formel (12.28) erhalten wir die Impulsantwort des entsprechenden digitalen Filters

Wo ist die Einheitsschrittfolge? Die Übertragungsfunktion des resultierenden digitalen Filters wird bestimmt, indem die -Transformation der durch Ausdruck (12.31) gegebenen Impulsantwort wie folgt ermittelt wird:

Durch den Vergleich der Ausdrücke (12.29) und (12.32) erhalten wir die Beziehung für den Übergang von analogen Filtern zu digitalen Filtern für die Impulsantwort-Invarianzmethode, die die Form hat

Digitaler Filterpol entsprechend analogem Filterpol

Beispiel 12.2. Der ursprüngliche analoge Filter hat die folgende Übertragungsfunktion:

Lösung. Schreiben wir die Funktion in Form einfacher Brüche

Aus den Gleichungen (12.33) folgt, dass es die Form hat

wobei T das Abtastintervall ist. Wenn wir den Ausdruck (12.36 a) vereinfachen, erhalten wir

Beispiel 12.3. Ein normalisierter Tschebyscheff-Tiefpassfilter zweiter Ordnung mit einer Welligkeit im Durchlassbereich von 3 dB hat eine Übertragungsfunktion der Form

Finden Sie die Übertragungsfunktion des entsprechenden digitalen Filters mithilfe der Impulsantwort-Invarianzmethode.

Lösung. Wenn wir die Funktion in Form von Faktoren schreiben, erhalten wir

Die Anwendung der Gleichungen (12.33) auf die resultierende Beziehung ergibt

Für c folgt aus Gleichung (12.39):

Reis. 12.10. Amplituden-Frequenz-Charakteristik eines Tschebyscheff-Filters zweiter Ordnung mit einer Ungleichmäßigkeit von 3 dB. analoger Filter, - digitaler Filter, digitaler Filter

Die Amplituden-Frequenz-Charakteristiken der durch die Ausdrücke (12 40) und (12.41) angegebenen Funktionen sind in Abb. dargestellt. 12 10

Erinnern wir uns daran, dass eine periodische Funktion der Variablen 0 mit einer Periode nicht periodisch ist. Der Hauptunterschied in den Eigenschaften analoger und digitaler Filter besteht darin, dass die Amplituden-Frequenz-Eigenschaften des resultierenden digitalen Filters von den Eigenschaften des ursprünglichen Analogfilters abweichen Filtern Sie in den Abschnitten, in denen die Kennlinie die Punkte erreicht, oder - Intervallabtastung. Wenn das Abtastintervall klein genug ist, beginnt die Abweichung bei einem Punkt nahe . Andernfalls beginnt die Abweichung viel früher. Ein geeigneter Fall ist in Abb. dargestellt. 12.10. Es ist zu beachten, dass die Grenzfrequenzen digitaler Filter punktuell liegen

wobei analoge Filter-Grenzfrequenzinformationen verwendet werden. Diese Grenzfrequenzen werden gemäß der folgenden Beziehung wiederholt:

Da die auf der Grundlage der Impulsantwort-Invarianzmethode erhaltene Impulsantwort eines digitalen Filters tatsächlich ein abgetastetes Analogon der Impulsantwort eines analogen Filters ist, ist die Frequenzantwort des digitalen Filters eine überlagerte Version der Frequenzantwort des analogen Filters. wie in Beziehung (11.115) festgestellt und der Einfachheit halber hier noch einmal angegeben:

Wenn die Abtastrate hoch genug ist, ist der Aliasing-Effekt minimal. In Abb. 12.10 für c zeigt, dass der Aliasing-Effekt, der sich in Form einer Abweichung der Frequenzcharakteristik von analogen und digitalen Filtern äußert, schwer zu unterscheiden ist. Wenn jedoch die Abtastrate nicht hoch genug ist, beispielsweise für den Fall (Abb. 12.10), beginnt der Überlagerungseffekt zu beeinflussen, da klar ist, dass er sich deutlich von der Substitution in Gleichungen (12.43) unterscheidet, die wir erhalten

Es ist zu beachten, dass die Gleichungen (12.44) den Zusammenhang zwischen den Übertragungsfunktionen der digitalen und entsprechenden analogen Filter für den Fall der Invarianz ihrer Impulseigenschaften herstellen.

Um die Eigenschaften mithilfe der Impulsantwort-Invarianzmethode zu untersuchen, ist es erforderlich, die beiden Anforderungen zu erfüllen

Bedingungen des Übergangsverfahrens (12.10) berücksichtigen, berücksichtigen Sie die Beziehung

und deshalb

Aus Abb. 12.11 folgt daraus, dass ein horizontaler Streifen mit einer Breite in der S-Ebene in der gesamten -Ebene angezeigt wird, d. h. die linke und rechte Hälfte dieses Streifens werden jeweils in einem Teil der -Ebene innerhalb und außerhalb des Einheitskreises angezeigt und die imaginäre Achse - im Einheitskreis. Aus Abb. 12.11 kann festgestellt werden, dass die Ursache des Überlagerungseffekts darin liegt, dass der Übergang (12.45) nicht eindeutig ist. Beispielsweise werden Punkte auf einen einzelnen Punkt abgebildet. Tatsächlich besagen die Beziehungen (12.45), dass die analoge Übertragungsfunktion in jeder Bandbreite der gesamten -Ebene überlagert wird, um eine digitale Übertragungsfunktion zu bilden. Daher handelt es sich bei der Impulsantwort-Invarianzmethode nicht um eine einfache lineare oder ähnliche Abbildung von der S-Ebene auf die -Ebene. Aufgrund des Aliasing-Effekts ist die Impulsantwort-Invarianzmethode nur auf Filter anwendbar, deren analoger Frequenzgang deutlich eingeschränkt ist und die Bedingung erfüllt

also im Fall von Tiefpass- und Bandpassfiltern.

Wie gezeigt, ist das auf der Impulsantwort-Invarianzmethode basierende Übergangsverfahren durch die Gleichungen (12.33) gegeben, die besagen, dass die Polanordnung des analogen Filters der folgenden Anordnung entspricht:

Somit stellen die Beziehungen (12.45) einen Zusammenhang zwischen der Platzierung der Pole der analogen und digitalen Filter her. Es ist jedoch absolut falsch zu sagen, dass die Verhältnisse

(Klicken Sie hier, um den Scan anzuzeigen)

Reis. 12.12. Diagramme der Pole und Nullstellen eines Lerner-Filters zweiter Ordnung: a – eine Variante eines analogen Filters, b – eine Variante eines digitalen Filters, der auf der Grundlage der Impulsantwort-Invarianzmethode erhalten wurde.

(12.45) Bestimmen Sie den Zusammenhang zwischen den Orten der Nullstellen digitaler und analoger Filter mit invarianten Impulsantworten. Ein geeignetes Beispiel ist der Follower.

Beispiel 12.4. Die Übertragungsfunktion des Analogfilters wird angegeben

wo Finden Sie die Position der Nullstellen und Pole des digitalen Filters, der auf der Grundlage der Invarianz der Impulsantwort erhalten wurde. Lösung. Die Erweiterung der Funktion in einfache Brüche ergibt

Die Übertragungsfunktion des entsprechenden digitalen Filters wird gemäß (12.33) in der Form angegeben

Aus Gleichung (12.50) ergibt sich die Position des endgültigen Nullpunkts des digitalen Filters durch

Wo ist die Position des Nullpunkts des analogen Filters? Die digitalen Filterpole sind jedoch wie folgt angeordnet:

Wo ist die Position der analogen Filterpole? Ein Diagramm der Anordnung der Pole und Nullstellen der analogen und entsprechenden digitalen Filter ist in Abb. dargestellt. 12.12.

Wie festgestellt wurde, gelten die Gleichungen (12.33) sowohl für reelle als auch für komplexe Pole. Für einen komplexen Pol ist es jedoch praktischer, ein Polpaar zusammen zu betrachten, bei dem der Balken über der Variablen verwendet wird, um die komplex konjugierte Größe anzuzeigen. Wenn wir die Gleichungen (12.33) entsprechend anwenden, erhalten wir Transformationspaare für die folgenden zwei Fälle zweiter Ordnung:

1. Wenn die Übertragungsfunktion eines analogen Filters in der Form angegeben ist

wo sich die Pole punktuell befinden

dann hat die Übertragungsfunktion des entsprechenden digitalen Filters die Form

2. Wenn die Funktion im Formular angegeben ist

dann folgt aus dem Übergangsverfahren (12.33) Folgendes

Beispiel 12.5. Ein analoger Butterworth-Tiefpassfilter dritter Ordnung ist durch die folgende Übertragungsfunktion gekennzeichnet:

Finden Sie die Übertragungsfunktion des entsprechenden digitalen Butterworth-Filters dritter Ordnung mithilfe der Impulsantwort-Invarianzmethode.

Lösung. Die Funktion kann geschrieben werden als

Aus den Gleichungen (12.33), (12.53)-(12.56) ergibt sich für den benötigten digitalen Filter die folgende Übertragungsfunktion:

Beispiel 12.6. Nehmen wir an, dass Ihr digitaler Tiefpassfilter die folgenden Bedingungen erfüllen muss:

a) Die Grenzfrequenz bei 3 dB ist rad.

b) Die Ungleichmäßigkeit des Amplituden-Frequenzgangs im Durchlassbereich beträgt nicht mehr als 0,1 dB für rad.

c) Die Dämpfung im Sperrbereich beträgt mehr als 30 dB für rad.

d) Die Amplituden-Frequenz-Kennlinie hat eine monoton fallende Form für

e) Abtastintervall

Finden Sie die Übertragungsfunktion des erforderlichen digitalen Filters.

Lösung. Der erste Schritt besteht darin, diese digitalen Kriterien in analoge zu übertragen. Dies kann dadurch erreicht werden, dass berücksichtigt wird, dass die Gleichungen (12–43) näherungsweise auf die Form reduziert werden, wenn T das Nyquist-Kriterium erfüllt

und deshalb

Nach der Beziehung (12.606) muss das gewünschte analoge Filter folgende Anforderungen erfüllen:

a) Die Grenzfrequenz liegt bei 3 dB