Beziehung zwischen trigonometrischen Funktionen desselben Winkels. Grundlegende trigonometrische Identitäten, ihre Formulierungen und Ableitung
„Satz der Sinus- und Kosinuswerte“ – 1) Schreiben Sie den Sinussatz für ein gegebenes Dreieck auf: Finden Sie den Winkel B. Schreiben Sie die Formel zur Berechnung auf: Sinussatz: Finden Sie die Länge der Seite BC. Sätze von Sinus und Cosinus. Die Seiten eines Dreiecks sind proportional zu den Sinuswerten der entgegengesetzten Winkel. 2) Schreiben Sie den Kosinussatz auf, um die Seite des MC zu berechnen: Unabhängige Arbeit:
„Trigonometrische Ungleichungen lösen“ – Alle y-Werte im Intervall MN. 1. Funktionsgraphen konstruieren: Die verbleibenden Intervalle. Die Gerade y=-1/2 schneidet die Sinuskurve in unendlich vielen Punkten und der trigonometrische Kreis schneidet im Punkt A in unendlich vielen Intervallen. Und auf einer Sinuskurve der Bereich der x-Werte, der dem Ursprung am nächsten liegt, für den sinx>-1/2 gilt,
„Trigonometrische Formeln“ – Formeln zur Umrechnung der Summe trigonometrischer Funktionen in ein Produkt. Formeln zur Umrechnung des Produkts trigonometrischer Funktionen in eine Summe. Additionsformeln. Durch trigonometrische Funktionen eines Winkels?. Doppelwinkelformeln. Indem wir die Gleichungen (3) und (4) Term für Term addieren, erhalten wir: Lassen Sie uns Hilfsformeln ableiten, die es uns ermöglichen, zu finden.
„Lösen der einfachsten trigonometrischen Ungleichungen“ – cos x. Methoden zur Lösung trigonometrischer Ungleichungen. Sünde x. Trigonometrische Ungleichungen sind Ungleichungen, die eine Variable im Argument einer trigonometrischen Funktion enthalten. Einfache trigonometrische Ungleichungen lösen.
„Sin und Cos“ – Stimmt es, dass der Kosinus von 6,5 größer als Null ist? Sinus von 60° ist gleich?? Stimmt das, weil? x - Schluck? x = 1? Ein Zweig der Mathematik, der die Eigenschaften von Sinus, Cosinus untersucht... Lektion über Algebra und grundlegende Analysis in der 10. Klasse. Trigonometrische Gleichungen und Ungleichungen lösen. Abszisse eines Punktes auf dem Einheitskreis. Das Verhältnis von Kosinus zu Sinus...
„Der Kosinussatz für ein Dreieck“ – Mündliche Arbeit. Unbekannte Elemente. Dreieck. Quadratische Seite eines Dreiecks. Geben Sie den Kosinussatz an. Satz. Der Kosinussatz. Probleme auf quadratischem Papier lösen. Ecken und Seiten. Geben Sie den Kosinussatz an. Aufgaben basierend auf fertigen Zeichnungen. Die in der Abbildung dargestellten Daten.
Insgesamt gibt es 21 Vorträge
In diesem Artikel werfen wir einen umfassenden Blick darauf. Grundlegende trigonometrische Identitäten sind Gleichheiten, die eine Verbindung zwischen Sinus, Cosinus, Tangens und Kotangens eines Winkels herstellen und es einem ermöglichen, jede dieser trigonometrischen Funktionen über eine bekannte andere zu finden.
Lassen Sie uns gleich die wichtigsten trigonometrischen Identitäten auflisten, die wir in diesem Artikel analysieren werden. Schreiben wir sie in eine Tabelle, und unten geben wir die Ergebnisse dieser Formeln an und geben die notwendigen Erklärungen.
Seitennavigation.
Beziehung zwischen Sinus und Cosinus eines Winkels
Manchmal geht es nicht um die in der obigen Tabelle aufgeführten wichtigsten trigonometrischen Identitäten, sondern um eine einzige grundlegende trigonometrische Identität Typ 
. Die Erklärung für diese Tatsache ist recht einfach: Die Gleichheiten werden aus der trigonometrischen Hauptidentität erhalten, nachdem beide Teile durch bzw. und die Gleichheiten dividiert wurden 
Und 
ergeben sich aus den Definitionen von Sinus, Cosinus, Tangens und Kotangens. Wir werden in den folgenden Abschnitten ausführlicher darauf eingehen.
Das heißt, von besonderem Interesse ist die Gleichheit, die den Namen der wichtigsten trigonometrischen Identität erhielt.
Bevor wir die trigonometrische Hauptidentität beweisen, geben wir ihre Formulierung an: Die Summe der Quadrate von Sinus und Cosinus eines Winkels ist identisch gleich eins. Jetzt lasst es uns beweisen.
Die grundlegende trigonometrische Identität wird sehr oft verwendet, wenn Konvertieren trigonometrischer Ausdrücke. Es ermöglicht, die Summe der Quadrate von Sinus und Cosinus eines Winkels durch eins zu ersetzen. Nicht seltener wird die grundlegende trigonometrische Identität in umgekehrter Reihenfolge verwendet: Die Einheit wird durch die Summe der Quadrate von Sinus und Cosinus eines beliebigen Winkels ersetzt.
Tangens und Kotangens durch Sinus und Cosinus
Identitäten, die Tangens und Kotangens mit Sinus und Cosinus eines Blickwinkels verbinden und 
ergeben sich unmittelbar aus den Definitionen von Sinus, Cosinus, Tangens und Kotangens. Tatsächlich ist der Sinus per Definition die Ordinate von y, der Kosinus die Abszisse von x und der Tangens das Verhältnis der Ordinate zur Abszisse, d. h. 
, und der Kotangens ist das Verhältnis der Abszisse zur Ordinate, d. h. 
.
Dank dieser Offensichtlichkeit der Identitäten und Tangens und Kotangens werden oft nicht durch das Verhältnis von Abszisse und Ordinate, sondern durch das Verhältnis von Sinus und Cosinus definiert. Der Tangens eines Winkels ist also das Verhältnis des Sinus zum Cosinus dieses Winkels, und der Kotangens ist das Verhältnis des Cosinus zum Sinus.
Zum Abschluss dieses Absatzes ist anzumerken, dass die Identitäten und finden für alle Winkel statt, bei denen die darin enthaltenen trigonometrischen Funktionen sinnvoll sind. Die Formel gilt also für alle außer (ansonsten hat der Nenner eine Null, und wir haben die Division durch Null nicht definiert) und die Formel - für alle, anders als wenn z irgendein Wert ist.
Beziehung zwischen Tangens und Kotangens
Eine noch offensichtlichere trigonometrische Identität als die beiden vorherigen ist die Identität, die Tangens und Kotangens eines Winkels der Form verbindet . Es ist klar, dass dies für alle anderen Winkel als gilt, da sonst entweder der Tangens oder der Kotangens nicht definiert sind.
Beweis der Formel sehr einfach. Per Definition und von wo 
. Der Beweis hätte etwas anders erfolgen können. Seit , Das 
.
Tangens und Kotangens des gleichen Winkels, bei dem sie sinnvoll sind, sind also .
LEKTIONSKARTE „ABHÄNGIGKEIT ZWISCHEN SINUS, KOSINUS UND TANGENT DES GLEICHEN WINKELS“
Student ________________________________________________________________________________
| 1. Ich kenne den Stoff aus früheren Lektionen | Punkte |
| Ich habe alle Fragen ohne Notizen richtig beantwortet. | |
| Ich habe ohne Notiz mit einem Fehler geantwortet. | |
| Ich antwortete, ohne mir Notizen zu machen, und machte mehr als einen Fehler. | |
| Ich habe alle Fragen anhand der Notizen richtig beantwortet. | |
| Ich antwortete anhand meiner Notizen, mit einem Fehler. | |
| Ich antwortete anhand meiner Notizen und machte mehr als einen Fehler |
| 2. Ich habe die Aufzeichnung der Beispiele abgeschlossen. | Punkte |
| Ich habe alle Aufgaben fehlerfrei erledigt | |
| Ich habe mit einem Fehler abgeschlossen | |
| Ich habe die Aufgaben erledigt und mehr als zwei Fehler gemacht |
| 3. Ich habe die Formel zur Ermittlung von Sinus und Cosinus abgeleitet | Punkte |
| Ich habe die Formeln richtig verstanden | |
| Ich habe die Formeln abgeleitet und einen Fehler gemacht | |
| Die Formeln habe ich mit Hilfe meines Lehrers abgeleitet |
| 4. Ich habe mein Wissen zum Thema: „Die Beziehung zwischen Sinus, Cosinus und Tangens desselben Winkels“ bei der Lösung unabhängiger Arbeiten angewendet | Punkte |
| Ich habe die Beispiele von Option 1 ohne Fehler gelöst. | |
| Ich habe die Beispiele von Option 1 gelöst und einen Fehler gemacht. | |
| Ich habe die Beispiele von Option 2 ohne Fehler gelöst. | |
| Ich habe die Beispiele von Option 2 gelöst und einen Fehler gemacht. | |
| Ich habe Beispiele 3 Optionen ohne Fehler gelöst | |
| Ich habe die Beispiele von Option 3 gelöst und einen Fehler gemacht. | |
| Ich habe Beispiele 4 Optionen ohne Fehler gelöst. | |
| Ich habe die Beispiele von Option 4 gelöst und einen Fehler gemacht. |
| 5. Bewerten Sie sich selbst: | |
| Ich habe die Herleitung der Formeln verstanden und kann mit einem Notizbuch und der Hilfe eines Lehrers Beispiele zu diesem Thema lösen. | |
| Ich habe die Herleitung der Formeln verstanden und kann Beispiele alleine ohne Notizbuch lösen, indem ich mir die Formeln einfach ansehe. | |
| Ich habe die Ableitung von Formeln verstanden und kann selbständig Beispiele lösen, ohne ein Notizbuch zu benötigen. Wenn ich eine Formel vergesse, kann ich sie selbst herleiten. |
Meine Punkte: __________
Maximale Punktzahl – 22
18 – 22 Punkte – Punktzahl „5“
15 – 17 Punkte – Punktzahl „4“
11–14 Punkte – Punktzahl „3“
Weniger als 11 Punkte - Sie müssen in den nächsten Tagen zu einem Beratungsgespräch kommen, der Stoff ist noch nicht beherrscht.
„Kurzplan“
Vera Anatolyevna Golovatova, Mathematiklehrerin
GB POE „Okhta College“
Zusammenfassung von zwei Lektionen für SchülerICH Kurs (10. Klasse) zum Thema:
„Die Beziehung zwischen Sinus, Cosinus und Tangens desselben Winkels“
Ziel: Untersuchen Sie die Beziehung zwischen Sinus, Cosinus und Tangens desselben Winkels.
Um dieses Ziel zu erreichen ist es notwendig:
Wissen:
Formulierungen von Definitionen grundlegender trigonometrischer Funktionen (Sinus, Cosinus und Tangens);
Vorzeichen trigonometrischer Funktionen nach Vierteln;
Wertemenge trigonometrischer Funktionen;
Grundformeln der Trigonometrie.
Verstehen:
dass die grundlegende trigonometrische Identität nur für dasselbe Argument verwendet werden kann;
Algorithmus zur Berechnung einer trigonometrischen Funktion durch eine andere.
Anwenden:
die Fähigkeit, die richtige Formel zur Lösung einer bestimmten Aufgabe richtig auszuwählen;
Fähigkeit, mit einfachen Brüchen zu arbeiten;
Fähigkeit, Transformationen trigonometrischer Ausdrücke durchzuführen.
Analyse:
Fehler in der Logik des Denkens analysieren.
Synthese:
Schlagen Sie Ihre eigene Lösungsmethode für Beispiele vor.
Erstellen Sie ein Kreuzworträtsel mit den gewonnenen Erkenntnissen.
Grad:
Kenntnisse und Fähigkeiten zu diesem Thema zur Verwendung in anderen Abschnitten der Algebra.
Ausrüstung: Layout eines trigonometrischen Kreises, Handouts mit Formeln und Wertetabellen trigonometrischer Funktionen, Computer, Multimedia-Projektor, Präsentation, Blätter mit Aufgaben zum selbstständigen Arbeiten.
Verwendete Quellen:
Algebra und Anfänge der Analysis: Lehrbuch für die Klassen 10-11. Allgemeinbildung Institutionen / Sh.A.Alimov, Yu.V. Sidorov et al. Bildung, 2006.
Open-Bank-Aufgaben zur Vorbereitung auf das Einheitliche Staatsexamen in Mathematik, 2011.
INTERNET-Netzwerkressourcen.
Kurzer Unterrichtsplan:
Zeit organisieren.
Grüße. Vermittlung des Unterrichtszwecks und des Unterrichtsplans – 3-5 Min.
Wissen und Fähigkeiten aktualisieren.
Den Schülern werden Unterrichtskarten ausgehändigt und Erklärungen zum Umgang damit gegeben.
Fragen werden auf dem Bildschirm angezeigt; Die Schüler schreiben die Antworten in ein Notizbuch. Der Lehrer zeigt die richtige Antwort auf dem Bildschirm an. Nach Abschluss der Umfrage tragen die Schüler Punkte zur Unterrichtskarte für bei Aufgaben Nr. 1 – 10 Minuten.
Erläuterung des neuen Materials.
Der Lehrer leitet die Formel für die grundlegende trigonometrische Identität ab – 5 Minuten.
Die Schüler werden gebeten, die Aufzeichnung der am Bildschirm angezeigten Beispiele selbstständig zu vervollständigen, die Richtigkeit der Antworten zu überprüfen und Punkte auf der Unterrichtskarte für hinzuzufügen Aufgaben Nr. 2 – 5 Minuten.
Im Notizbuch werden die Schüler aufgefordert, unabhängig voneinander Sinus durch Cosinus und Cosinus durch Sinus aus der trigonometrischen Grundidentität auszudrücken. Die richtige Antwort wird auf dem Bildschirm angezeigt, die Schüler überprüfen sie und fügen der Unterrichtskarte Punkte hinzu Aufgaben Nr. 3 – 5-7 Min.
Der Lehrer löst Beispiele an der Tafel unter Verwendung der grundlegenden trigonometrischen Identität. Die Schüler beantworten während der Erklärung die Fragen des Lehrers und notieren Beispiele in ihren Heften – 15 Minuten.
Der Lehrer leitet Formeln ab, die den Zusammenhang zwischen Tangens und Kotangens zeigen, die Schüler beteiligen sich aktiv an der Ableitung von Formeln, beantworten Fragen und machen sich Notizen in einem Notizbuch - 5 Minuten.
Der Lehrer leitet Formeln ab, die den Zusammenhang zwischen Tangens und Cosinus, zwischen Sinus und Kotangens zeigen – 5 Minuten.
Die Schüler werden nach Belieben an die Tafel gerufen und lösen mit Hilfe des Lehrers Beispiele mithilfe eines Algorithmus. Alle anderen schreiben die Fragen auf und beantworten sie bei Bedarf - 10 Minuten.
Vertiefung des Gelernten
Am Ende der Unterrichtsstunde werden die richtigen Antworten auf dem Bildschirm angezeigt, die Schüler überprüfen ihre Antworten und tragen Punkte zur Unterrichtskarte für ein Aufgaben Nr. 4 – 20 Minuten.
Hausaufgaben: Die Schüler schreiben Hausaufgaben in ihre Hefte - 3 Minuten.
Dokumentinhalte anzeigen
"Betrachtung"
Nachdem ich Seminare zu RNS besucht und eine Lektion anhand einer Technologiekarte gehalten hatte, wurde mir klar, dass das Bewertungssystem das größtmögliche Interesse der Schüler an einem bestimmten Thema weckt. In meinem Fall sind das die Grundformeln der Trigonometrie.
Trigonometrie wird von Studierenden sehr oft nicht wahrgenommen, nicht so sehr wegen ihrer Komplexität, sondern wegen der großen Anzahl an Formeln, mit denen man arbeiten muss.
Es ist schwer, nach einer Unterrichtsstunde mit einer Technologiekarte unglaubliche Erfolge und Ergebnisse zu erwarten, aber mir scheint, dass die Vorteile des Bewertungssystems beim Studium der Trigonometrie und der Mathematik im Allgemeinen wie folgt sind:
es wurde möglich, sowohl die Arbeit im Klassenzimmer als auch die selbstständige, systematische Arbeit der Studierenden zu Hause zu organisieren und zu unterstützen;
Anwesenheit und Disziplin im Unterricht sollten erhöht werden;
die Motivation für Bildungsaktivitäten steigt;
Stresssituationen bei ungenügenden Noten werden reduziert;
Die kreative Einstellung zur Arbeit wird gefördert.
Der einzige Nachteil von RNS (wie es mir scheint) ist der große Arbeitsaufwand für den Lehrer, aber das ist Arbeit für Ergebnisse. Nach einer einzigen Unterrichtsstunde, die mit diesem System unterrichtet wurde, fragen sich die Schüler ständig, ob wir so weiterarbeiten werden. Es bedeutet, dass sie von etwas süchtig waren. Und wir müssen weiterarbeiten.
Dokumentinhalte anzeigen
"Selbstständige Arbeit"
SELBSTSTÄNDIGE ARBEIT
Welches Level Sie auch wählen, überprüfen Sie zunächst sorgfältig alle Aufgaben, die ich Ihnen gegeben habe, und erledigen Sie dann die Aufgabe, die dem von Ihnen gewählten Level entspricht (Bevor Sie Aufgaben mit vier Optionen erhalten, entspricht die Anzahl der Optionen dem Grad des Selbstwertgefühls.)
1 Option
Anweisungen:
Anweisungen:
Lösen Sie dieses Beispiel selbst: 
Option 2
Hinweis: Um die Kosinusfunktion zu bestimmen, verwenden Sie Formel (3) aus der heutigen Lektion. Vergessen Sie nicht, das Zeichen zu bestimmen, das vor der Wurzel erscheinen soll. Um die Werte von Tangens und Kotangens zu berechnen, können Sie die Definition dieser Funktionen verwenden oder die Formeln verwenden, die wir heute im Unterricht entwickelt haben.
Notiz. Gruppieren Sie den ersten und dritten Term des Ausdrucks und entfernen Sie den gemeinsamen Faktor aus Klammern....
Option 3
Option 4
Präsentationsinhalte anzeigen
"Präsentation"
Wiederholung:
1. In welchem Viertel liegt der Winkel?
1 Bogenmaß und was ist ungefähr gleich?
Im ersten Quartal 1 rad. 57,3°
2. Welches Wort fehlt in der Definition der Sinusfunktion?
Sinus des Winkels genannt ………… Punkte des Einheitskreises.
ORDINATE
3. Welches Wort fehlt in der Definition der Kosinusfunktion?
Kosinus des Winkels angerufen
………… Punkte des Einheitskreises.
ABSZISSE
4. Vervollständigen Sie die Formel:
tg
5. Bestimmen Sie das Vorzeichen des Produkts:
tg
6. Welchen Wert kann der Sinus annehmen?
oder
7. Berechnen Sie:
j
B(x;y)
R
Y=Sünde
Ö
X
x=cos
Vervollständigen Sie die Aufnahme:
X
j
X
j
X
X
X
j
X
j
X
X
- Ich habe das Thema verstanden und kann Beispiele mit dem Algorithmus lösen, indem ich auf das Notizbuch schaue, aber mit Hilfe von Leitfragen (Karte - Anleitung).
- Ich habe das Thema verstanden und kann Beispiele mithilfe des Algorithmus lösen, indem ich auf das Notizbuch schaue und die Anweisungen des Lehrers befolge.
- + Ich habe das Thema verstanden und kann mit Blick auf das Notizbuch Beispiele mithilfe des Algorithmus lösen, ohne Leitfragen oder Anweisungen.
- + Ich habe das Thema verstanden und kann Beispiele mit dem Algorithmus lösen, ohne auf das Notizbuch zu schauen.
Option 1:
Option 3:
Option 2:
Option 4:
Trigonometrische Identitäten- Dies sind Gleichheiten, die eine Beziehung zwischen Sinus, Cosinus, Tangens und Kotangens eines Winkels herstellen, die es Ihnen ermöglicht, jede dieser Funktionen zu finden, sofern eine andere bekannt ist.
tg \alpha = \frac(\sin \alpha)(\cos \alpha), \enspace ctg \alpha = \frac(\cos \alpha)(\sin \alpha)
tg \alpha \cdot ctg \alpha = 1
Diese Identität besagt, dass die Summe des Quadrats des Sinus eines Winkels und des Quadrats des Kosinus eines Winkels gleich eins ist, was es in der Praxis ermöglicht, den Sinus eines Winkels zu berechnen, wenn sein Kosinus bekannt ist, und umgekehrt .
Bei der Konvertierung trigonometrischer Ausdrücke wird diese Identität sehr häufig verwendet, wodurch Sie die Summe der Quadrate von Kosinus und Sinus eines Winkels durch eins ersetzen und den Ersetzungsvorgang auch in umgekehrter Reihenfolge durchführen können.
Tangens und Kotangens mithilfe von Sinus und Cosinus ermitteln
tg \alpha = \frac(\sin \alpha)(\cos \alpha),\enspace
Diese Identitäten werden aus den Definitionen von Sinus, Cosinus, Tangens und Kotangens gebildet. Wenn man es sich genau ansieht, dann ist die Ordinate y per Definition ein Sinus und die Abszisse x ein Kosinus. Dann ist der Tangens gleich dem Verhältnis \frac(y)(x)=\frac(\sin \alpha)(\cos \alpha) und das Verhältnis \frac(x)(y)=\frac(\cos \alpha)(\sin \alpha)- wird ein Kotangens sein.
Fügen wir hinzu, dass die Identitäten nur für solche Winkel \alpha gelten, bei denen die darin enthaltenen trigonometrischen Funktionen einen Sinn ergeben, ctg \alpha=\frac(\cos \alpha)(\sin \alpha).
Zum Beispiel: tg \alpha = \frac(\sin \alpha)(\cos \alpha) gilt für andere Winkel \alpha als \frac(\pi)(2)+\pi z, A ctg \alpha=\frac(\cos \alpha)(\sin \alpha)- Für einen anderen Winkel \alpha als \pi z ist z eine ganze Zahl.
Beziehung zwischen Tangens und Kotangens
tg \alpha \cdot ctg \alpha=1
Diese Identität gilt nur für andere Winkel \alpha als \frac(\pi)(2) z. Andernfalls wird weder Kotangens noch Tangens bestimmt.
Basierend auf den oben genannten Punkten erhalten wir das tg \alpha = \frac(y)(x), A ctg \alpha=\frac(x)(y). Es folgt dem tg \alpha \cdot ctg \alpha = \frac(y)(x) \cdot \frac(x)(y)=1. Daher sind Tangens und Kotangens desselben Winkels, bei dem sie sinnvoll sind, zueinander inverse Zahlen.
Beziehungen zwischen Tangens und Cosinus, Kotangens und Sinus
tg^(2) \alpha + 1=\frac(1)(\cos^(2) \alpha)- Die Summe des Quadrats des Tangens des Winkels \alpha und 1 ist gleich dem Umkehrquadrat des Kosinus dieses Winkels. Diese Identität gilt für alle \alpha außer \frac(\pi)(2)+ \pi z.
1+ctg^(2) \alpha=\frac(1)(\sin^(2)\alpha)- Die Summe aus 1 und dem Quadrat des Kotangens des Winkels \alpha ist gleich dem Umkehrquadrat des Sinus des gegebenen Winkels. Diese Identität gilt für jedes \alpha, das sich von \pi z unterscheidet.
Beispiele mit Lösungen für Probleme unter Verwendung trigonometrischer Identitäten
Beispiel 1
Finden Sie \sin \alpha und tg \alpha if \cos \alpha=-\frac12 Und \frac(\pi)(2)< \alpha < \pi ;
Lösung anzeigen
Lösung
Die Funktionen \sin\alpha und \cos\alpha hängen durch die Formel zusammen \sin^(2)\alpha + \cos^(2) \alpha = 1. Einsetzen in diese Formel \cos \alpha = -\frac12, wir bekommen:
\sin^(2)\alpha + \left (-\frac12 \right)^2 = 1
Diese Gleichung hat zwei Lösungen:
\sin \alpha = \pm \sqrt(1-\frac14) = \pm \frac(\sqrt 3)(2)
Nach Bedingung \frac(\pi)(2)< \alpha < \pi . Im zweiten Viertel ist der Sinus also positiv \sin \alpha = \frac(\sqrt 3)(2).
Um tan \alpha zu finden, verwenden wir die Formel tg \alpha = \frac(\sin \alpha)(\cos \alpha)
tg \alpha = \frac(\sqrt 3)(2) : \frac12 = \sqrt 3
Beispiel 2
Finden Sie \cos \alpha und ctg \alpha, wenn und \frac(\pi)(2)< \alpha < \pi .
Lösung anzeigen
Lösung
Einsetzen in die Formel \sin^(2)\alpha + \cos^(2) \alpha = 1 angegebene Nummer \sin \alpha=\frac(\sqrt3)(2), wir bekommen \left (\frac(\sqrt3)(2)\right)^(2) + \cos^(2) \alpha = 1. Diese Gleichung hat zwei Lösungen \cos \alpha = \pm \sqrt(1-\frac34)=\pm\sqrt\frac14.
Nach Bedingung \frac(\pi)(2)< \alpha < \pi . Im zweiten Viertel ist der Kosinus also negativ \cos \alpha = -\sqrt\frac14=-\frac12.
Um ctg \alpha zu finden, verwenden wir die Formel ctg \alpha = \frac(\cos \alpha)(\sin \alpha). Wir kennen die entsprechenden Werte.
ctg \alpha = -\frac12: \frac(\sqrt3)(2) = -\frac(1)(\sqrt 3).
Thema: Trigonometrische Formeln (25 Stunden)
Lektion 6 – 7: Die Beziehung zwischen Sinus, Cosinus und Tangens desselben Winkels.
Ziel: Untersuchen Sie die Beziehung zwischen Sinus, Cosinus und Tangens desselben Winkels. Um dieses Ziel zu erreichen ist es notwendig:
- Wissen:
- Formulierungen von Definitionen grundlegender trigonometrischer Funktionen (Sinus, Cosinus und Tangens); Vorzeichen trigonometrischer Funktionen nach Vierteln; Wertemenge trigonometrischer Funktionen; Grundformeln der Trigonometrie.
- Verstehen:
- dass die grundlegende trigonometrische Identität nur für dasselbe Argument verwendet werden kann; Algorithmus zur Berechnung einer trigonometrischen Funktion durch eine andere.
- Anwenden:
- die Fähigkeit, die richtige Formel zur Lösung einer bestimmten Aufgabe richtig auszuwählen; Fähigkeit, mit einfachen Brüchen zu arbeiten; Fähigkeit, Transformationen trigonometrischer Ausdrücke durchzuführen.
- Analyse:
- Fehler in der Logik des Denkens analysieren.
- Synthese:
- Schlagen Sie Ihre eigene Lösungsmethode für Beispiele vor. Erstellen Sie ein Kreuzworträtsel mit den gewonnenen Erkenntnissen.
- Grad:
- Kenntnisse und Fähigkeiten zu diesem Thema zur Verwendung in anderen Abschnitten der Algebra.
- Zeit organisieren.
- Wissen und Fähigkeiten aktualisieren.
- In welchem Viertel liegt ein Winkel von 1 Bogenmaß und wie groß ist er ungefähr?
- Welches Wort fehlt in der Definition der Sinusfunktion?
- Welches Wort fehlt in der Definition der Kosinusfunktion?
- Welche Werte kann der Sinus annehmen?
() - Erläuterung des neuen Materials.
Stellen wir uns einen Einheitskreis mit dem Mittelpunkt im Punkt O dar. Nehmen wir an, dass durch Drehen des Radius OA, gleich R, um einen Winkel , der Radius OB erhalten wird (Abb. 5). Dann per Definition 
Wo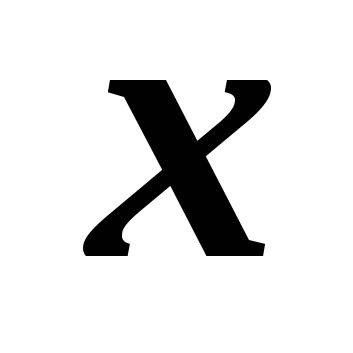 
– Abszisse von Punkt B, 
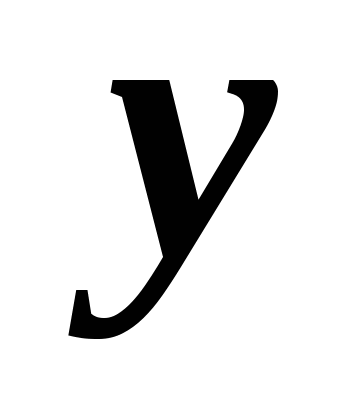– seine Ordinate. Daraus folgt, dass Punkt B zum Kreis gehört. Daher erfüllen seine Koordinaten die Gleichung 
Ausnutzen, was wir bekommen 
(1).
Wir haben eine Gleichheit erhalten, die für alle darin enthaltenen Buchstabenwerte gilt. Wie nennt man solche Gleichheiten? Das ist richtig – Identitäten. Gleichheit (1) heißt grundlegende trigonometrische Identität. In Gleichung (1) kann jeden Wert annehmen. Vervollständigen Sie die Aufnahme selbst: 1.
Bitte überprüfen Sie, ob Ihre Eingabe korrekt ist. Fügen Sie Ihrer Unterrichtskarte Punkte hinzu für Aufgaben Nr. 2. Lass uns weitermachen. Wir haben die wichtigste trigonometrische Identität abgeleitet, aber warum brauchen wir sie? Das ist richtig – den Kosinuswert aus einem bekannten Sinuswert zu ermitteln und umgekehrt. Jetzt können Sie und ich immer die grundlegende trigonometrische Identität verwenden, aber die Hauptsache ist das gleiche Argument. Im Notizbuch werden die Schüler aufgefordert, unabhängig voneinander Sinus durch Cosinus und Cosinus durch Sinus aus der trigonometrischen Grundidentität auszudrücken. Zwei Schüler werden zur Kontrolle an die Tafel gerufen. Einer wird gebeten, den Sinus durch den Kosinus auszudrücken, der zweite - den Kosinus durch den Sinus. Die richtige Antwort wird auf dem Bildschirm angezeigt:
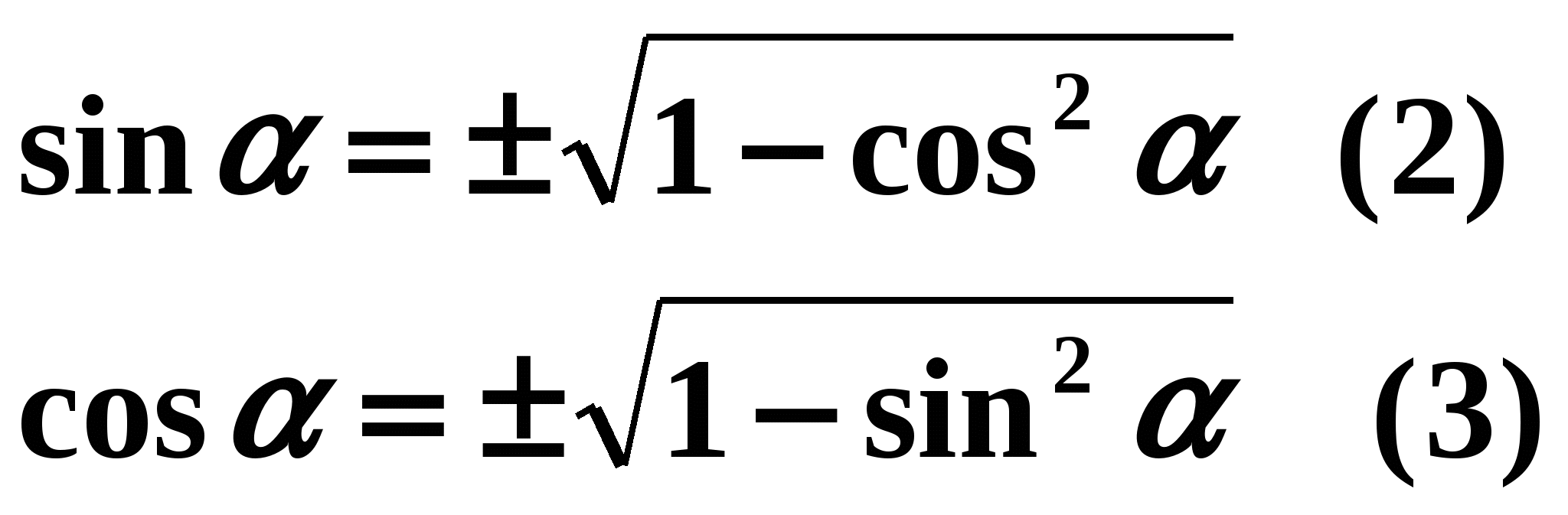Die Schüler überprüfen ihre Antworten und fügen der Unterrichtskarte Punkte hinzu Aufgaben Nr. 3.
Wovon hängt in diesen Formeln das Vorzeichen vor der Wurzel ab? (Es hängt davon ab, in welchem Quadranten sich der Winkel der trigonometrischen Funktion befindet, die wir definieren). Beispiel 1 . Berechnung
Wenn 
Bestimmen Sie das Viertel, in dem sich der Winkel befindet 
. Viertel – III. Denken Sie daran, dass der Sinus im dritten Viertel negativ ist, d. h. in Formel (2) müssen Sie das „-“-Zeichen vor die Wurzel setzen: Beispiel 2.
Berechnung 
Wenn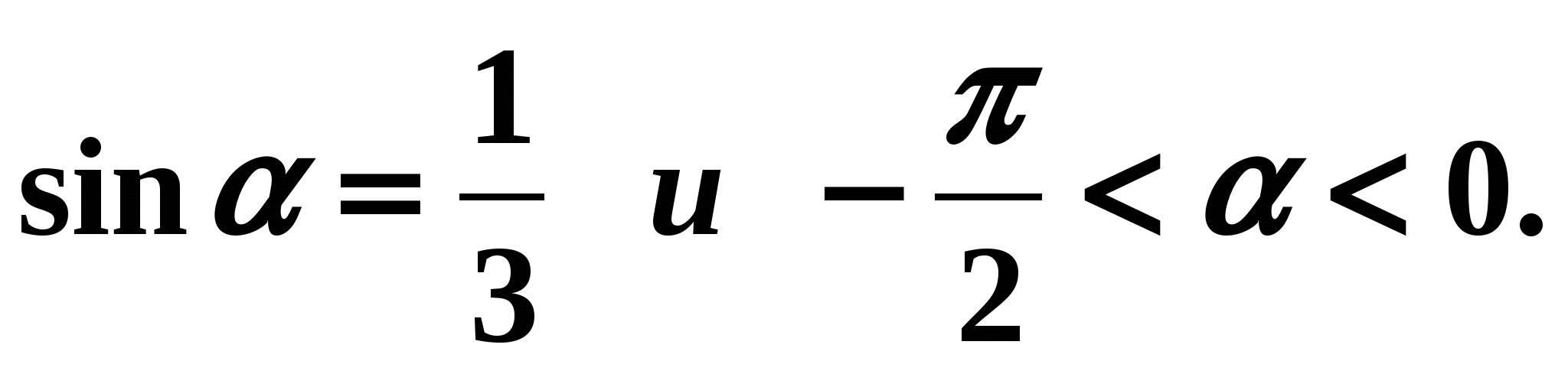 
Wir bestimmen das Viertel, in dem der Winkel liegt. Viertel – IV, der Kosinus im vierten Viertel ist positiv. Daher ist in Formel (3) das „+“-Zeichen vor der Wurzel erforderlich: Finden wir es jetzt heraus Beziehung zwischen Tangens und Kotangens. Per Definition von Tangens und Kotangens
Wenn wir diese Gleichungen multiplizieren, erhalten wir:
Aus Gleichung (4) können wir ausdrücken
durch 
umgekehrt: 
Die Gleichungen (4) – (6) gelten für alle Werte, für die
Sinn machen, d.h. wann 
Lassen Sie uns nun Formeln ableiten, die die Beziehung zwischen Tangens und Kosinus sowie Kotangens und Sinus desselben Arguments ausdrücken. Division beider Seiten der Gleichheit (1) durch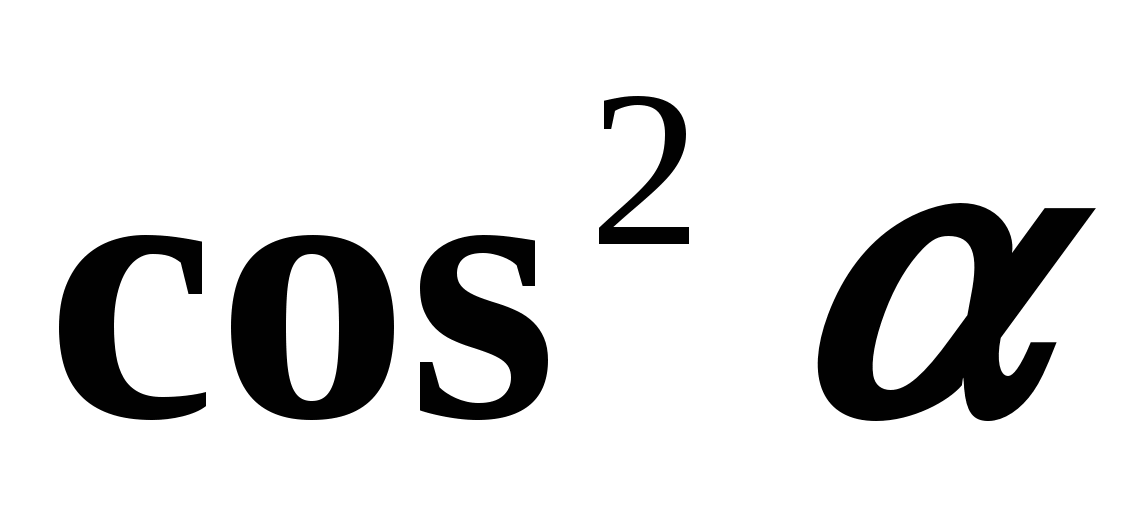 
, wir bekommen: 
diese.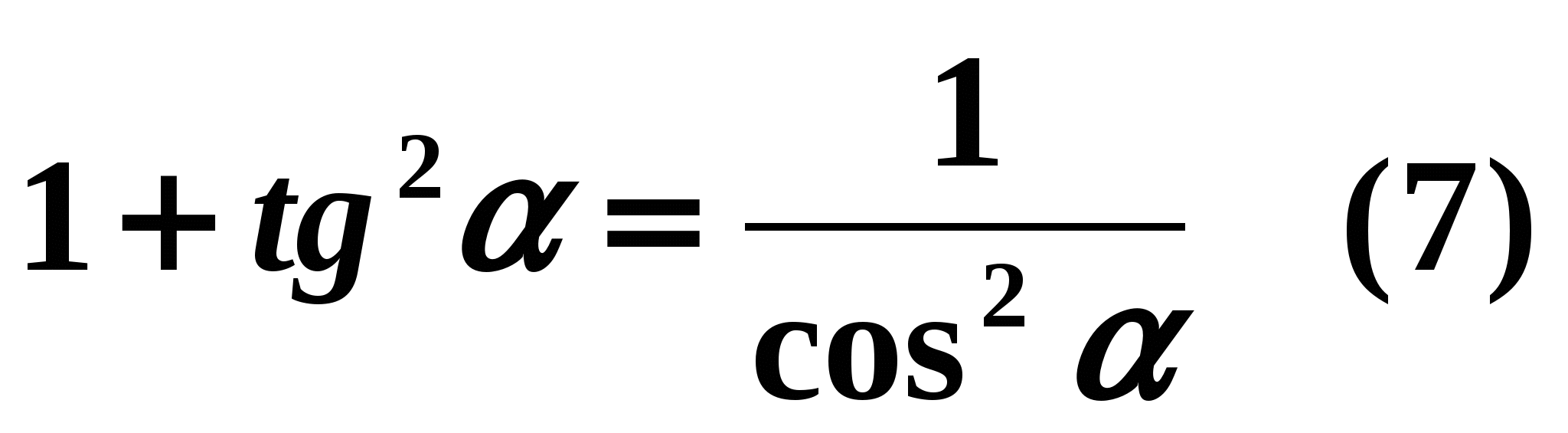 
Wenn beide Seiten der Gleichheit (1) durch geteilt werden
, dann haben wir: 
diese. 
Schauen wir uns Beispiele für die Verwendung der abgeleiteten Formeln an, um die Werte trigonometrischer Funktionen aus einem bekannten Wert einer von ihnen zu ermitteln.
Beispiel 1. Finden wir heraus, ob das bekannt ist
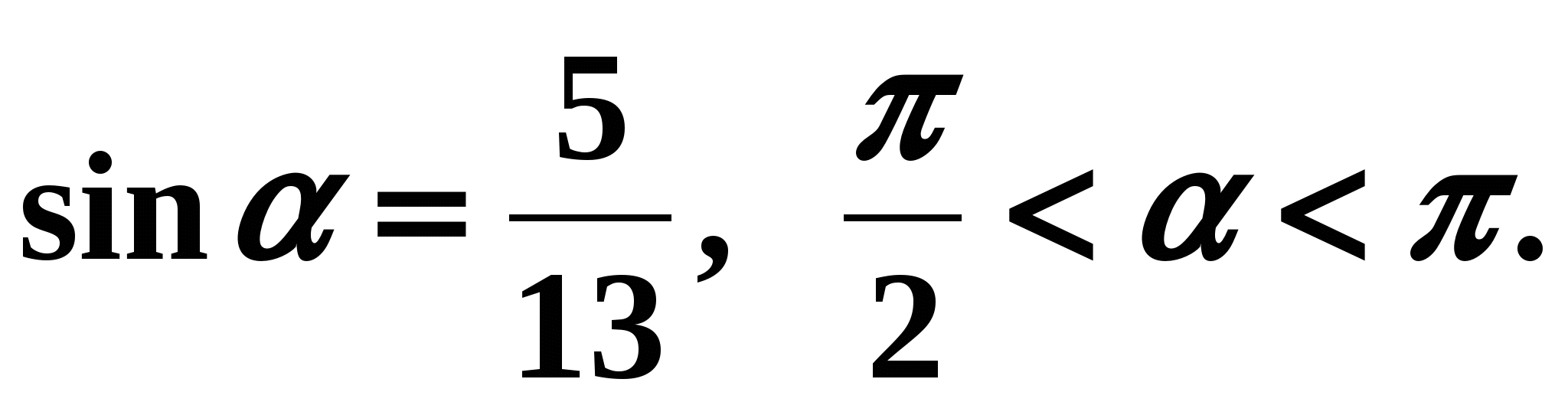Lösung: 
- Um den Kotangens des Winkels zu ermitteln, ist es praktisch, die Formel (6) zu verwenden:
Antwort: Beispiel 2. Es ist bekannt, dass
. Lassen Sie uns alle anderen trigonometrischen Funktionen finden. Lösung: - Verwenden wir die Formel (7).
Wir haben:
, 
. Gemäß den Bedingungen des Problems ist der Winkel der Winkel von einem Viertel, also ist sein Kosinus positiv. Bedeutet 
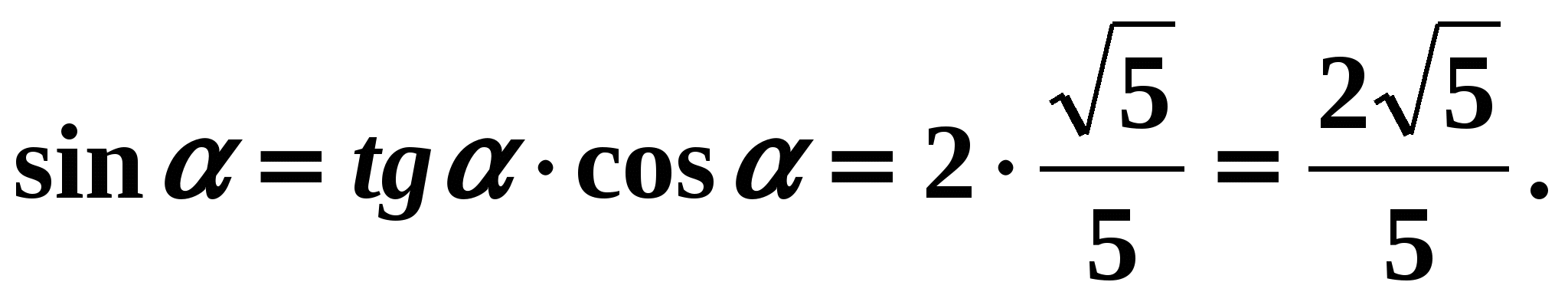
Antwort:
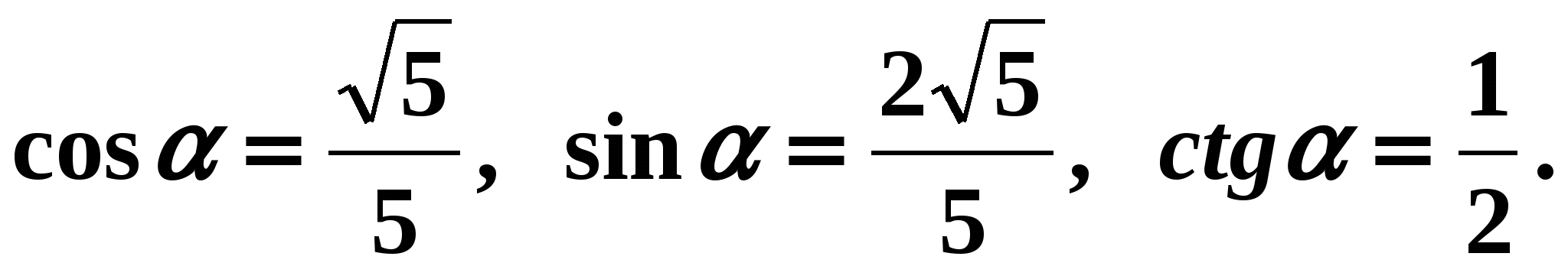Festgelegte Beziehungen zwischen trigonometrischen Funktionen desselben Arguments ermöglichen die Vereinfachung trigonometrischer Ausdrücke. Beispiel 3. Vereinfachen wir den Ausdruck:
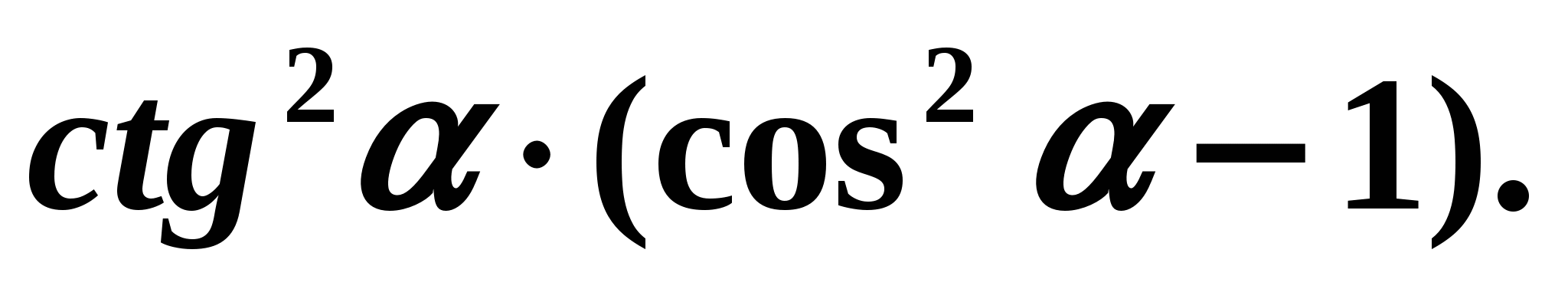Lösung: Verwenden wir die Formeln: 
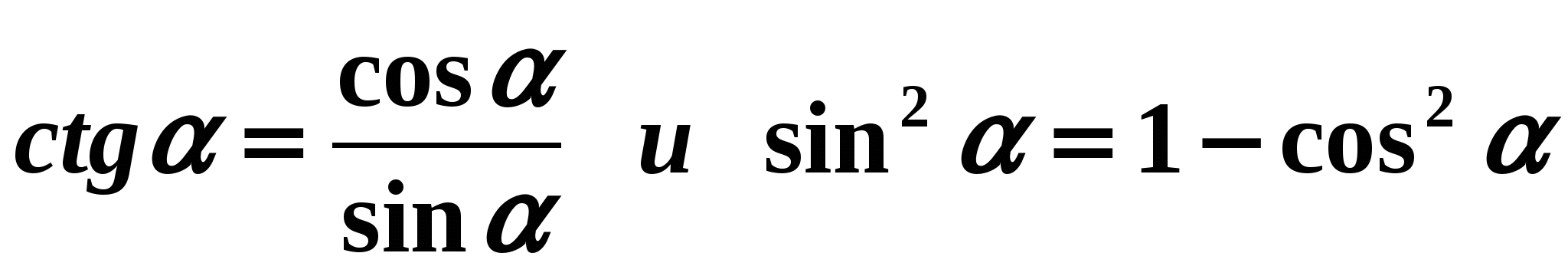. Wir bekommen: - Konsolidierung.
Und jetzt werden Selbstbewertungsrubriken zu diesem Thema auf dem Bildschirm angezeigt. Markieren Sie, welches Niveau Sie heute erreichen möchten.
Ich habe das Thema verstanden und kann Beispiele mit dem Algorithmus lösen, indem ich auf das Notizbuch schaue, aber mit Hilfe von Leitfragen (Karte - Anleitung).
Ich habe das Thema verstanden und kann Beispiele mithilfe des Algorithmus lösen, indem ich auf das Notizbuch schaue und die Anweisungen des Lehrers befolge.
Ich habe das Thema verstanden und kann Beispiele mit dem Algorithmus lösen, indem ich auf das Notizbuch schaue, ohne Leitfragen oder Anweisungen.
Ich habe das Thema verstanden und kann Beispiele mit dem Algorithmus lösen, ohne auf das Notizbuch zu schauen.
Welches Level Sie auch wählen, überprüfen Sie zunächst alle Aufgaben, die ich Ihnen gegeben habe, sorgfältig und erledigen Sie dann die Aufgabe, die dem von Ihnen gewählten Level entspricht (vor Ihnen liegen Aufgaben in vier Optionen, die Nummer der Option entspricht der Ebenen des Selbstwertgefühls.)
1 Option
Anweisungen:
Option 4
Nun Leute, schauen wir uns die Antworten an. Die richtigen Antworten werden auf dem Bildschirm angezeigt, die Schüler überprüfen ihre Arbeit und fügen Punkte zur Lektionskarte hinzu Aufgaben Nr. 4. Bewerten Sie sich selbst anhand der Lektionskarte. Berechnen Sie Ihre Punkte und tragen Sie sie auf die Karte ein.
- Hausaufgaben.
- Notieren Sie alle abgeleiteten Formeln im Nachschlagewerk. Laut Lehrbuch Nr. 459 (3, 5), Nr. 460 (1)
