Definieren Sie eine stetige Funktion. Zwei große Grenzen. Wir verwenden die Cauchy-Definition

1. Einleitung.

2. Bestimmung der Stetigkeit einer Funktion.

3. Klassifizierung von Haltepunkten

4. Eigenschaften stetiger Funktionen.

5. Die wirtschaftliche Bedeutung von Kontinuität.

6. Fazit.

10.1. Einführung

Immer wenn wir die unvermeidlichen Veränderungen in der Welt um uns herum im Laufe der Zeit beurteilen, versuchen wir, die laufenden Prozesse zu analysieren, um ihre wichtigsten Merkmale hervorzuheben. Eine der ersten Fragen, die sich auf diesem Weg stellen, ist: Wie es treten Veränderungen auf, die für dieses Phänomen charakteristisch sind - ständig oder diskret, d.h. krampfhaft. Fällt der Wechselkurs ab oder bricht er gleichmäßig zusammen, gibt es eine allmähliche Entwicklung oder einen revolutionären Sprung? Um qualitative und quantitative Einschätzungen des Geschehens zu vereinheitlichen, sollte man vom spezifischen Inhalt abstrahieren und das Problem im Hinblick auf die funktionale Abhängigkeit untersuchen. Dies kann durch die Grenzwerttheorie erfolgen, die wir in der letzten Vorlesung besprochen haben.

10.2. Definition der Stetigkeit einer Funktion

Die Stetigkeit einer Funktion hängt intuitiv mit der Tatsache zusammen, dass ihr Graph eine kontinuierliche Kurve ist, die nirgendwo bricht. Wir zeichnen einen Graphen einer solchen Funktion, ohne den Stift vom Papier zu nehmen. Wenn eine Funktion in einer Tabelle angegeben ist, kann ihre Kontinuität streng genommen nicht beurteilt werden, da für einen bestimmten Tabellenschritt das Verhalten der Funktion in Intervallen nicht definiert ist.

In der Realität tritt mit Kontinuität der folgende Umstand ein: wenn die Parameter, die die Situation charakterisieren Ein wenig dann ändern Ein wenig die Situation wird sich ändern. Wichtig ist hier nicht, dass sich die Situation ändert, sondern dass sie sich „ein wenig“ ändert.

Formulieren wir den Begriff der Kontinuität in der Sprache der Inkremente. Lassen Sie ein Phänomen durch eine Funktion und einen Punkt beschreiben A gehört zum Definitionsbereich der Funktion. Der Unterschied heißt Argumentinkrement am Punkt A, Unterschied - Funktionsinkrement am Punkt A.

Definition 10.1.Funktion kontinuierlich an einem Punkt a, wenn es an dieser Stelle definiert ist und ein infinitesimales Inkrement im Argument einem infinitesimalen Inkrement in der Funktion entspricht:

Beispiel 10.1. Untersuchen Sie die Stetigkeit der Funktion an dem Punkt.

Lösung. Lassen Sie uns einen Graphen der Funktion erstellen und die Inkremente D darauf markieren X und D j(Abb. 10.1).

Die Grafik zeigt, dass das Inkrement D umso kleiner ist X, desto weniger D j. Lassen Sie uns dies analytisch zeigen. Das Inkrement des Arguments ist gleich, dann ist das Inkrement der Funktion an dieser Stelle gleich

Daraus ist klar, dass wenn, dann und:

.

Lassen Sie uns die Stetigkeit einer Funktion noch einmal definieren.

Definition 10.2.Die Funktion wird aufgerufen kontinuierlich an Punkt a wenn:

1) es ist am Punkt a und einigen seiner Umgebungen definiert;

2) einseitige Grenzen existieren und einander gleich sind:

;

3) Grenze der Funktion bei x® a ist an dieser Stelle gleich dem Wert der Funktion:

.

Wenn mindestens eine dieser Bedingungen verletzt ist, wird die Funktion als durchlaufen bezeichnet Lücke.

Diese Definition dient zur Herstellung der Kontinuität an einem Punkt. Wenn wir seinem Algorithmus folgen und die Übereinstimmungen und Diskrepanzen zwischen den Anforderungen der Definition und einem konkreten Beispiel beachten, können wir schlussfolgern, dass die Funktion an einem Punkt stetig ist.

In Definition 2 kommt die Idee der Nähe deutlich zum Vorschein, als wir das Konzept der Grenze eingeführt haben. Mit einer unbegrenzten Annäherung an das Argument X auf den Grenzwert A, kontinuierlich an einem Punkt A Funktion F(X) kommt dem Grenzwert beliebig nahe F(A).

10.3. Klassifizierung von Bruchstellen

Die Punkte, an denen die Kontinuitätsbedingungen einer Funktion verletzt werden, werden aufgerufen Bruchstellen diese Funktion. Wenn X 0 ist der Bruchpunkt der Funktion; mindestens eine der Bedingungen für die Kontinuität der Funktion ist nicht erfüllt. Betrachten Sie das folgende Beispiel.

1. Die Funktion wird in einer bestimmten Umgebung des Punktes definiert A, aber nicht an der Stelle selbst definiert A. Beispielsweise ist die Funktion am Punkt nicht definiert A=2, erfährt daher eine Diskontinuität (siehe Abb. 10.2).

Reis. 10.2 Abb. 10.3

2. Die Funktion ist an einem Punkt definiert A und in einigen seiner Umgebungen existieren seine einseitigen Grenzen, sind aber einander nicht gleich: , dann erfährt die Funktion eine Diskontinuität. Zum Beispiel die Funktion

ist am Punkt definiert, erfährt aber an der Funktion eine Diskontinuität (siehe Abb. 10.3), weil

Und ().

3. Die Funktion ist an einem Punkt definiert A und in einer Umgebung davon gibt es eine Grenze der Funktion bei , aber diese Grenze ist nicht gleich dem Wert der Funktion an diesem Punkt A:

.

Zum Beispiel die Funktion (siehe Abb. 10.4)

Hier ist der Bruchpunkt:

,

Alle Unstetigkeitsstellen werden in entfernbare Unstetigkeitsstellen, Unstetigkeitsstellen erster und zweiter Art, unterteilt.

Definition 10.1. Der Bruchpunkt wird Punkt genannt reparierbare Lücke , wenn es an dieser Stelle links und rechts endliche Grenzen der Funktion gibt, die einander gleich sind:

.

Der Grenzwert der Funktion an diesem Punkt existiert, ist jedoch nicht gleich dem Wert der Funktion am Grenzpunkt (wenn die Funktion am Grenzpunkt definiert ist) oder die Funktion am Grenzpunkt ist nicht definiert.

In Abb. 10.4 An der Stelle werden die Kontinuitätsbedingungen verletzt und die Funktion weist eine Diskontinuität auf. Punkt im Diagramm (0; 1) ausgehöhlt. Diese Lücke lässt sich jedoch leicht schließen – es reicht aus, diese Funktion neu zu definieren und sie an dieser Stelle auf ihren Grenzwert zu setzen, d.h. setzen . Daher werden solche Lücken als entfernbar bezeichnet.

Definition 10.2. Die Sollbruchstelle heißt Unstetigkeitsstelle 1. Art , wenn an dieser Stelle links und rechts endliche Grenzen der Funktion existieren, diese aber einander nicht gleich sind:

.

An diesem Punkt soll die Funktion erfahren sein Sprung.

In Abb. 10.3 Die Funktion weist im Punkt eine Unstetigkeit 1. Art auf. Die linken und rechten Grenzen sind an dieser Stelle gleich:

Und .

Der Sprung der Funktion am Unstetigkeitspunkt ist gleich.

Es ist unmöglich, eine solche Funktion als stetig zu definieren. Der Graph besteht aus zwei durch einen Sprung getrennten Halblinien.

Definition 10.3. Die Sollbruchstelle heißt Unstetigkeitsstelle 2. Art , wenn mindestens einer der einseitigen Grenzen der Funktion (links oder rechts) nicht existiert oder gleich unendlich ist.

In Abbildung 10.3 weist die Funktion an einem Punkt eine Unstetigkeit 2. Art auf. Die betrachtete Funktion at ist unendlich groß und hat weder rechts noch links einen endlichen Grenzwert. Daher besteht an dieser Stelle keine Notwendigkeit, von Kontinuität zu sprechen.

Beispiel 10.2. Erstellen Sie ein Diagramm und bestimmen Sie die Art der Bruchpunkte:

Lösung. Lassen Sie uns die Funktion grafisch darstellen F(X) (Abbildung 10.5).

Die Abbildung zeigt, dass die ursprüngliche Funktion drei Diskontinuitätspunkte hat: , X 2 = 1,
X 3 = 3. Betrachten wir sie der Reihe nach.

Deshalb hat der Punkt Bruch der 2. Art.

a) Die Funktion ist an dieser Stelle definiert: F(1) = –1.

B) , ,

diese. am Punkt X 2 = 1 verfügbar reparierbare Lücke. Durch Neudefinition des Funktionswerts an dieser Stelle: F(1) = 5, die Diskontinuität wird beseitigt und die Funktion an diesem Punkt wird stetig.

a) Die Funktion ist an dieser Stelle definiert: F(3) = 1.

Also, auf den Punkt gebracht X 1 = 3 verfügbar Bruch der 1. Art. Die Funktion erfährt an dieser Stelle einen Sprung gleich D j= –2–1 = –3.

10.4. Eigenschaften stetiger Funktionen

Unter Berücksichtigung der entsprechenden Eigenschaften von Grenzwerten kommen wir zu dem Schluss, dass auch Funktionen, die das Ergebnis arithmetischer Operationen an am selben Punkt stetigen Funktionen sind, stetig sind. Notiz:

1) wenn die Funktionen und im Punkt stetig sind A, dann sind die Funktionen , und (sofern ) an dieser Stelle ebenfalls stetig;

2) wenn die Funktion im Punkt stetig ist A und die Funktion im Punkt stetig ist, dann ist die komplexe Funktion im Punkt stetig A Und

,

diese. Das Grenzwertzeichen kann unter das Vorzeichen einer stetigen Funktion gestellt werden.

Sie sagen, dass Eine Funktion ist auf einer Menge stetig, wenn sie an jedem Punkt dieser Menge stetig ist. Der Graph einer solchen Funktion ist eine durchgehende Linie, die mit einem Federstrich durchgestrichen werden kann.

Alle großen Elementarfunktionen sind an allen Stellen, an denen sie definiert sind, stetig.

Funktionen, kontinuierlich auf dem Segment haben eine Reihe wichtiger charakteristischer Eigenschaften. Lassen Sie uns Sätze formulieren, die einige dieser Eigenschaften ausdrücken.

Satz 10.1 (Satz von Weierstrass ). Wenn eine Funktion auf einem Segment stetig ist, erreicht sie auf diesem Segment ihre minimalen und maximalen Werte.

Satz 10.2 (Satz von Cauchy ). Wenn eine Funktion in einem Intervall stetig ist, dann liegen in diesem Intervall alle Zwischenwerte zwischen dem kleinsten und dem größten Wert.

Aus dem Satz von Cauchy folgt die folgende wichtige Eigenschaft.

Satz 10.3. Wenn eine Funktion auf einem Segment stetig ist und an den Enden des Segments Werte unterschiedlichen Vorzeichens annimmt, dann gibt es zwischen a und b einen Punkt c, an dem die Funktion verschwindet:.

Die geometrische Bedeutung dieses Theorems liegt auf der Hand: Wenn der Graph einer stetigen Funktion von der unteren Halbebene zur oberen Halbebene (oder umgekehrt) geht, dann schneidet er zumindest an einem Punkt die Achse Ochse(Abb. 10.6).

Beispiel 10.3. Berechnen Sie ungefähr die Wurzel der Gleichung

, (d. h. ungefähr ersetzen) Polynom des entsprechenden Grades.

Dies ist eine für die Praxis sehr wichtige Eigenschaft kontinuierlicher Funktionen. Stetige Funktionen werden beispielsweise sehr oft durch Tabellen (Beobachtungs- oder experimentelle Daten) spezifiziert. Dann können Sie mit einer Methode die tabellarische Funktion durch ein Polynom ersetzen. Gemäß Satz 10.3 kann dies immer mit ausreichend hoher Genauigkeit erfolgen. Das Arbeiten mit einer analytisch definierten Funktion (insbesondere einem Polynom) ist viel einfacher.

10.5. Ökonomische Bedeutung von Kontinuität

Die meisten in der Volkswirtschaftslehre verwendeten Funktionen sind kontinuierlich, und dies ermöglicht es, recht aussagekräftige Aussagen zum ökonomischen Inhalt zu treffen.

Betrachten Sie zur Veranschaulichung das folgende Beispiel.

Steuersatz N hat ungefähr die gleiche Grafik wie in Abb. 10.7a.

An den Enden der Intervalle ist es diskontinuierlich und diese Diskontinuitäten sind von der 1. Art. Allerdings ist die Höhe der Einkommensteuer selbst P(Abb. 10.7b) ist eine kontinuierliche Funktion des Jahreseinkommens Q. Daraus folgt insbesondere, dass sich, wenn sich die Jahreseinkommen zweier Personen nur unwesentlich unterscheiden, auch die Differenz der zu zahlenden Einkommensteuerbeträge unwesentlich unterscheiden muss. Interessant ist, dass der Umstand von der überwiegenden Mehrheit der Menschen als völlig natürlich wahrgenommen wird, worüber sie nicht einmal nachdenken.

10.6. Abschluss

Gönnen wir uns zum Schluss einen kleinen Rückzug.

So lässt sich die traurige Beobachtung der Alten anschaulich ausdrücken:

Sic transit Gloria mundi...

(So vergeht die irdische Herrlichkeit …)

Feierabend -

Dieses Thema gehört zum Abschnitt:

Funktionsbegriff

Das Konzept der Funktion.. alles fließt und alles verändert sich Heraklit.. Tabelle x x x x y y y y..

Wenn Sie zusätzliches Material zu diesem Thema benötigen oder nicht gefunden haben, was Sie gesucht haben, empfehlen wir Ihnen die Suche in unserer Werkdatenbank:

Was machen wir mit dem erhaltenen Material:

Wenn dieses Material für Sie nützlich war, können Sie es auf Ihrer Seite in sozialen Netzwerken speichern:

Definition. Die Funktion y = f(x) sei am Punkt x0 und in einigen seiner Umgebungen definiert. Die Funktion y = f(x) wird aufgerufen kontinuierlich im Punkt x0, Wenn:

1. existiert
2. Dieser Grenzwert ist gleich dem Wert der Funktion am Punkt x0:

Bei der Definition des Grenzwerts wurde betont, dass f(x) nicht am Punkt x0 definiert werden darf, und wenn es an diesem Punkt definiert wird, dann ist der Wert von f(x0) in keiner Weise an der Bestimmung des Grenzwerts beteiligt. Bei der Bestimmung der Kontinuität ist es von grundlegender Bedeutung, dass f(x0) existiert, und dieser Wert muss gleich lim f(x) sein.

Definition. Die Funktion y = f(x) sei am Punkt x0 und in einigen seiner Umgebungen definiert. Eine Funktion f(x) heißt stetig an einem Punkt x0, wenn es für alle ε>0 eine positive Zahl δ gibt, so dass für alle x in der δ-Umgebung des Punktes x0 (also |x-x0|) gilt
Dabei wird berücksichtigt, dass der Wert des Grenzwertes gleich f(x0) sein muss, daher entfällt im Vergleich zur Definition des Grenzwertes die Bedingung der Punktion der δ-Umgebung 0
Lassen Sie uns eine weitere (zur vorherigen äquivalente) Definition in Bezug auf Inkremente geben. Bezeichnen wir Δх = x - x0; wir nennen diesen Wert das Inkrement des Arguments. Da x->x0, dann Δx->0, d. h. Δx - b.m. (unendliche) Menge. Bezeichnen wir Δу = f(x)-f(x0), wir nennen diesen Wert das Inkrement der Funktion, da |Δу| sollte (für ausreichend kleines |Δх|) kleiner als eine beliebige Zahl ε>0 sein, dann ist Δу- auch b.m. Wert also

Definition. Die Funktion y = f(x) sei am Punkt x0 und in einigen seiner Umgebungen definiert. Die Funktion f(x) wird aufgerufen kontinuierlich im Punkt x0, wenn ein infinitesimales Inkrement im Argument einem infinitesimalen Inkrement in der Funktion entspricht.

Definition. Die Funktion f(x), die im Punkt x0 nicht stetig ist, diskontinuierlich genannt an dieser Stelle.

Definition. Eine Funktion f(x) heißt stetig auf einer Menge X, wenn sie an jedem Punkt dieser Menge stetig ist.

Satz über die Stetigkeit einer Summe, eines Produkts, eines Quotienten

Satz über den Grenzübergang im Vorzeichen einer stetigen Funktion

Satz über die Stetigkeit der Superposition stetiger Funktionen

Die Funktion f(x) sei in einem Intervall definiert und in diesem Intervall monoton. Dann kann f(x) auf diesem Segment nur Unstetigkeitspunkte erster Art haben.

Zwischenwertsatz. Wenn die Funktion f(x) auf einem Segment stetig ist und an zwei Punkten a und b (a ist kleiner als b) ungleiche Werte annimmt A = f(a) ≠ B = f(b), dann für jede Zahl C zwischen A und B gibt es einen Punkt c ∈, an dem der Wert der Funktion gleich C ist: f(c) = C.

Satz über die Beschränktheit einer stetigen Funktion auf einem Intervall. Wenn eine Funktion f(x) auf einem Intervall stetig ist, dann ist sie auf dieses Intervall beschränkt.

Satz über das Erreichen von Minimal- und Maximalwerten. Wenn die Funktion f(x) in einem Intervall stetig ist, erreicht sie in diesem Intervall ihre untere und obere Grenze.

Satz über die Stetigkeit der Umkehrfunktion. Die Funktion y=f(x) sei stetig und im Intervall [a,b] streng steigend (fallend). Dann gibt es auf dem Segment eine Umkehrfunktion x = g(y), ebenfalls monoton steigend (fallend) und stetig.

Bestimmen der Stetigkeit einer Funktion an einem Punkt
Funktion f (X) angerufen kontinuierlich im Punkt x 0 Nachbarschaft U (x0) dieser Punkt, und wenn die Grenze als x zu x tendiert 0 existiert und ist gleich dem Wert der Funktion bei x 0 :
.

Dies impliziert, dass x 0 - Das ist der Endpunkt. Der darin enthaltene Funktionswert kann nur eine endliche Zahl sein.

Definition der Kontinuität rechts (links)
Funktion f (X) angerufen kontinuierlich rechts (links) im Punkt x 0 , wenn es in einer rechtsseitigen (linksseitigen) Umgebung dieses Punktes definiert ist und wenn die rechte (linke) Grenze am Punkt x liegt 0 gleich dem Funktionswert bei x 0 :
.

Beispiele

Beispiel 1

Beweisen Sie mithilfe der Heine- und Cauchy-Definitionen, dass die Funktion für alle x stetig ist.

Es sei eine beliebige Zahl. Beweisen wir, dass die gegebene Funktion im Punkt stetig ist. Die Funktion ist für alle x definiert. Daher ist es an einem Punkt und in jeder seiner Umgebungen definiert.

Wir verwenden Heines Definition

Lasst uns verwenden. Es gebe eine beliebige Folge, die gegen Folgendes konvergiert: . Wenn wir die Eigenschaft des Grenzwerts eines Produkts von Folgen anwenden, erhalten wir:
.
Da es eine beliebige Folge gibt, die gegen konvergiert, dann
.
Kontinuität ist bewiesen.

Wir verwenden die Cauchy-Definition

Lasst uns verwenden.
Betrachten wir den Fall. Wir haben das Recht, die Funktion in jeder Umgebung des Punktes zu betrachten. Deshalb gehen wir davon aus
(A1.1) .

Wenden wir die Formel an:
.
Unter Berücksichtigung von (A1.1) nehmen wir folgende Schätzung vor:

;
(A1.2) .

Unter Anwendung von (A1.2) schätzen wir den absoluten Wert der Differenz:
;
(A1.3) .
.
Gemäß den Eigenschaften von Ungleichungen gilt: Wenn (A1.3) erfüllt ist, wenn und wenn, dann.

.

Schauen wir uns nun den Punkt an. In diesem Fall
.
.

.
Das bedeutet, dass die Funktion im Punkt stetig ist.

Auf ähnliche Weise kann man beweisen, dass die Funktion, bei der n eine natürliche Zahl ist, auf der gesamten reellen Achse stetig ist.

Beispiel 2

Beweisen Sie, dass die Funktion für alle stetig ist.

Die angegebene Funktion ist unter definiert. Beweisen wir, dass es an diesem Punkt stetig ist.

Betrachten wir den Fall.
Wir haben das Recht, die Funktion in jeder Umgebung des Punktes zu betrachten. Deshalb gehen wir davon aus
(A2.1) .

Wenden wir die Formel an:
(A2.2) .
Sagen wir es. Dann
.

Unter Berücksichtigung von (A2.1) nehmen wir folgende Schätzung vor:


.
Also,
.

Unter Anwendung dieser Ungleichung und unter Verwendung von (A2.2) schätzen wir den Unterschied:

.
Also,
(A2.3) .

Wir führen positive Zahlen ein und verbinden sie mit den folgenden Beziehungen:
.
Gemäß den Eigenschaften von Ungleichungen gilt: Wenn (A2.3) erfüllt ist, wenn und wenn, dann.

Das bedeutet, dass es für jedes Positive immer ein gibt. Dann ist für alle x, die die Ungleichung erfüllen, automatisch die folgende Ungleichung erfüllt:
.
Das bedeutet, dass die Funktion im Punkt stetig ist.

Schauen wir uns nun den Punkt an. Wir müssen zeigen, dass die gegebene Funktion an diesem Punkt rechts stetig ist. In diesem Fall
.
Geben Sie positive Zahlen ein und:
.

Dies zeigt, dass es für jedes Positive immer . Dann gilt für alle x, so dass die folgende Ungleichung gilt:
.
Es bedeutet das. Das heißt, die Funktion ist im Punkt rechts stetig.

Auf ähnliche Weise kann man beweisen, dass die Funktion, wobei n eine natürliche Zahl ist, für stetig ist.

Verweise:
O.I. Besov. Vorlesungen über mathematische Analysis. Teil 1. Moskau, 2004.
L.D. Kudryavtsev. Kurs der mathematischen Analyse. Band 1. Moskau, 2003.
CM. Nikolski. Kurs der mathematischen Analyse. Band 1. Moskau, 1983.

In dieser Lektion lernen wir, wie man die Stetigkeit einer Funktion ermittelt. Wir werden dies tun, indem wir Grenzen verwenden, noch dazu einseitige – rechts und links, die überhaupt nicht gruselig sind, obwohl sie als und geschrieben sind.

Aber was ist überhaupt Stetigkeit einer Funktion? Bis wir zu einer strengen Definition kommen, ist es am einfachsten, sich eine Linie vorzustellen, die man zeichnen kann, ohne den Bleistift vom Papier zu nehmen. Wird eine solche Linie gezogen, dann ist sie durchgehend. Diese Linie ist der Graph einer stetigen Funktion.

Grafisch gesehen ist eine Funktion an einem Punkt stetig, wenn ihr Graph an diesem Punkt nicht „bricht“. Der Graph einer solchen kontinuierlichen Funktion ist in der folgenden Abbildung dargestellt.

Bestimmung der Stetigkeit einer Funktion durch einen Grenzwert. Eine Funktion ist an einem Punkt stetig, wenn drei Bedingungen erfüllt sind:

1. Die Funktion wird am Punkt definiert.

Wenn mindestens eine der aufgeführten Bedingungen nicht erfüllt ist, ist die Funktion an der Stelle nicht stetig. In diesem Fall sagt man, dass die Funktion eine Diskontinuität aufweist, und die Punkte im Graphen, an denen der Graph unterbrochen wird, werden Diskontinuitätspunkte der Funktion genannt. Der Graph einer solchen Funktion, die am Punkt x=2 eine Diskontinuität aufweist, ist in der folgenden Abbildung dargestellt.

Beispiel 1. Funktion F(X) ist wie folgt definiert:

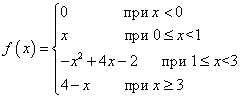
Wird diese Funktion an jedem der Randpunkte ihrer Zweige, also an den Punkten, stetig sein? X = 0 , X = 1 , X = 3 ?

Lösung. Wir prüfen alle drei Bedingungen für die Stetigkeit einer Funktion an jedem Randpunkt. Die erste Bedingung ist erfüllt, seit was Funktion definiert an jedem der Randpunkte ergibt sich aus der Definition der Funktion. Es bleiben noch die beiden verbleibenden Bedingungen zu prüfen.

Punkt X= 0 . Lassen Sie uns an dieser Stelle die linke Grenze ermitteln:

.

Finden wir die rechte Grenze:

X= 0 muss für den Zweig der Funktion gefunden werden, der diesen Punkt enthält, also den zweiten Zweig. Wir finden sie:

Wie wir sehen können, ist der Grenzwert der Funktion und der Wert der Funktion an dem Punkt X= 0 sind gleich. Daher ist die Funktion im Punkt stetig X = 0 .

Punkt X= 1 . Lassen Sie uns an dieser Stelle die linke Grenze ermitteln:

Finden wir die rechte Grenze:

Grenzwert einer Funktion und Wert einer Funktion an einem Punkt X= 1 muss für den Zweig der Funktion gefunden werden, der diesen Punkt enthält, also den zweiten Zweig. Wir finden sie:

.

Grenzwert einer Funktion und Wert einer Funktion an einem Punkt X= 1 sind gleich. Daher ist die Funktion im Punkt stetig X = 1 .

Punkt X= 3 . Lassen Sie uns an dieser Stelle die linke Grenze ermitteln:

Finden wir die rechte Grenze:

Grenzwert einer Funktion und Wert einer Funktion an einem Punkt X= 3 muss für den Zweig der Funktion gefunden werden, der diesen Punkt enthält, also den zweiten Zweig. Wir finden sie:

.

Grenzwert einer Funktion und Wert einer Funktion an einem Punkt X= 3 sind gleich. Daher ist die Funktion im Punkt stetig X = 3 .

Die wichtigste Schlussfolgerung: Diese Funktion ist an jedem Randpunkt stetig.

Stellen Sie selbst die Stetigkeit einer Funktion an einem Punkt fest und schauen Sie sich dann die Lösung an

Eine kontinuierliche Änderung einer Funktion kann als eine allmähliche Änderung ohne Sprünge definiert werden, bei der eine kleine Änderung des Arguments eine kleine Änderung der Funktion nach sich zieht.

Lassen Sie uns diesen kontinuierlichen Funktionswechsel anhand eines Beispiels veranschaulichen.

Lassen Sie ein Gewicht an einem Faden über dem Tisch hängen. Unter dem Einfluss dieser Belastung dehnt sich der Faden, also die Strecke l Die Last am Aufhängepunkt des Fadens ist eine Funktion der Masse der Last M, also l = F(M) , M≥0 .

Wenn Sie die Masse der Last leicht ändern, ändert sich auch der Abstand l wird sich wenig ändern: kleine Änderungen M kleine Änderungen entsprechen l. Liegt die Masse der Last jedoch nahe an der Zugfestigkeit des Fadens, kann eine geringfügige Erhöhung der Masse der Last zum Bruch des Fadens führen: Abstand l steigt schlagartig an und entspricht dem Abstand vom Aufhängepunkt zur Tischoberfläche. Graph einer Funktion l = F(M) in der Abbildung dargestellt. An einem Abschnitt ist dieser Graph eine durchgehende (durchgezogene) Linie, an einem Punkt ist er unterbrochen. Das Ergebnis ist ein Graph, der aus zwei Zweigen besteht. An allen Punkten außer der Funktion l = F(M) ist kontinuierlich, weist aber an einem Punkt eine Diskontinuität auf.

Die Untersuchung einer Funktion auf Kontinuität kann entweder eine eigenständige Aufgabe oder eine der Phasen einer vollständigen Untersuchung der Funktion und der Erstellung ihres Graphen sein.

Stetigkeit einer Funktion auf einem Intervall

Lassen Sie die Funktion j = F(X) definiert im Intervall ] A, B[ und ist an jedem Punkt dieses Intervalls stetig. Dann heißt es stetig im Intervall ] A, B[ . Das Konzept der Stetigkeit einer Funktion auf Intervallen der Form ]- ∞ wird ähnlich definiert: B[ , ]A, + ∞[ , ]- ∞, + ∞[ . Lassen Sie uns nun die Funktion ausführen j = F(X) definiert auf dem Intervall [ A, B] . Der Unterschied zwischen einem Intervall und einem Segment: Die Grenzpunkte eines Intervalls sind nicht im Intervall enthalten, aber die Grenzpunkte eines Segments sind im Segment enthalten. Hier ist die sogenannte einseitige Kontinuität zu erwähnen: am Punkt A, verbleibt auf dem Segment [ A, B] können wir nur von rechts und auf den Punkt kommen B- nur links. Man sagt, die Funktion sei stetig im Intervall [ A, B] , wenn es an allen inneren Punkten dieses Segments stetig ist, rechts am Punkt stetig A und bleibt an der Stelle kontinuierlich B.

Ein Beispiel für eine stetige Funktion kann jede der Elementarfunktionen sein. Jede Elementarfunktion ist in jedem Intervall, in dem sie definiert ist, stetig. Beispielsweise sind die Funktionen und in jedem Intervall stetig [ A, B], die Funktion ist stetig im Intervall [ 0 , B] ist die Funktion auf jedem Segment, das keinen Punkt enthält, stetig A = 2 .

Beispiel 4. Untersuchen Sie die Funktion auf Kontinuität.

Lösung. Lassen Sie uns die erste Bedingung überprüfen. Die Funktion ist an den Punkten 3 und 3 nicht definiert. Mindestens eine der Bedingungen für die Kontinuität der Funktion entlang der gesamten Zahlengeraden ist nicht erfüllt. Daher ist diese Funktion in den Intervallen stetig

.

Beispiel 5. Bestimmen Sie den Wert des Parameters A durchgehend durchgehend Definitionsbereich Funktion

Lösung.

Finden wir die rechte Grenze bei:

.

Offensichtlich ist der Wert an der Stelle X= 2 sollte gleich sein Axt :

A = 1,5 .

Beispiel 6. Bestimmen Sie, bei welchen Parameterwerten A Und B durchgehend durchgehend Definitionsbereich Funktion

Lösung.
Suchen wir den linksseitigen Grenzwert der Funktion an der Stelle:

.

Daher muss der Wert an der Stelle 1 sein:

Suchen wir die linke Funktion an der Stelle:

Offensichtlich sollte der Wert der Funktion an einem Punkt gleich sein:

Antwort: Die Funktion ist über den gesamten Definitionsbereich stetig, wenn A = 1; B = -3 .

Grundlegende Eigenschaften stetiger Funktionen

Die Mathematik kam zum Konzept einer stetigen Funktion, indem sie zunächst verschiedene Bewegungsgesetze untersuchte. Raum und Zeit sind unendlich und Abhängigkeiten beispielsweise Wege S von Zeit T, gesetzlich ausgedrückt S = F(T) , gibt ein Beispiel für eine kontinuierliche Funktionen F(T). Auch die Temperatur des erhitzten Wassers ändert sich kontinuierlich, sie ist ebenfalls eine kontinuierliche Funktion der Zeit: T = F(T) .

In der mathematischen Analyse werden einige Eigenschaften stetiger Funktionen bewiesen. Lassen Sie uns die wichtigsten dieser Eigenschaften vorstellen.

1. Wenn eine in einem Intervall kontinuierliche Funktion an den Enden des Intervalls Werte mit unterschiedlichen Vorzeichen annimmt, nimmt sie an einem bestimmten Punkt dieses Intervalls einen Wert gleich Null an. In einer formelleren Aussage wird diese Eigenschaft in einem Satz angegeben, der als erster Bolzano-Cauchy-Satz bekannt ist.

2. Funktion F(X), kontinuierlich im Intervall [ A, B] , nimmt alle Zwischenwerte zwischen den Werten an den Endpunkten, also zwischen F(A) Und F(B). In einer formelleren Aussage wird diese Eigenschaft in einem Satz angegeben, der als zweiter Bolzano-Cauchy-Satz bekannt ist.