Sin 45 Grad Tisch. Eigenschaften von Tangens und Kotangens. Ausdrücke durch hyperbolische Funktionen
Referenzdaten für Tangens (tg x) und Kotangens (ctg x). Geometrische Definition, Eigenschaften, Diagramme, Formeln. Tabelle der Tangenten und Kotangenten, Ableitungen, Integrale, Reihenentwicklungen. Ausdrücke durch komplexe Variablen. Zusammenhang mit hyperbolischen Funktionen.
Geometrische Definition

|BD| - Länge des Kreisbogens mit Mittelpunkt im Punkt A.
α ist der im Bogenmaß ausgedrückte Winkel.
Tangente ( tan α) ist eine trigonometrische Funktion, die vom Winkel α zwischen der Hypotenuse und dem Schenkel eines rechtwinkligen Dreiecks abhängt und dem Verhältnis der Länge des gegenüberliegenden Schenkels |BC| entspricht zur Länge des benachbarten Beins |AB| .
Kotangens ( ctg α) ist eine trigonometrische Funktion, die vom Winkel α zwischen der Hypotenuse und dem Schenkel eines rechtwinkligen Dreiecks abhängt und dem Verhältnis der Länge des angrenzenden Schenkels |AB| entspricht zur Länge des gegenüberliegenden Beins |BC| .
Tangente
Wo N- ganz.
In der westlichen Literatur wird Tangens wie folgt bezeichnet:
.
;
;
.
Graph der Tangensfunktion, y = tan x

Kotangens
Wo N- ganz.
In der westlichen Literatur wird Kotangens wie folgt bezeichnet:
.
Folgende Notationen werden ebenfalls akzeptiert:
;
;
.
Diagramm der Kotangensfunktion, y = ctg x

Eigenschaften von Tangens und Kotangens
Periodizität
Funktionen y = tg x und y = ctg x sind periodisch mit der Periode π.
Parität
Die Tangens- und Kotangensfunktionen sind ungerade.
Definitions- und Wertebereiche, zunehmend, abnehmend
Die Tangens- und Kotangensfunktionen sind in ihrem Definitionsbereich stetig (siehe Kontinuitätsnachweis). Die Haupteigenschaften von Tangens und Kotangens sind in der Tabelle dargestellt ( N- ganz).
| y = tg x | y = ctg x | |
| Umfang und Kontinuität | ||
| Wertebereich | -∞ < y < +∞ | -∞ < y < +∞ |
| Zunehmend | - | |
| Absteigend | - | |
| Extreme | - | - |
| Nullen, y = 0 | ||
| Schnittpunkte mit der Ordinatenachse, x = 0 | y = 0 | - |
Formeln
Ausdrücke mit Sinus und Cosinus
;
;
;
;
;
Formeln für Tangens und Kotangens aus Summe und Differenz
Die restlichen Formeln sind beispielsweise leicht zu erhalten
Produkt von Tangenten
Formel für Summe und Differenz von Tangenten
Diese Tabelle zeigt die Werte von Tangenten und Kotangenten für bestimmte Werte des Arguments. 
Ausdrücke mit komplexen Zahlen
Ausdrücke durch hyperbolische Funktionen
;
;
Derivate
; .
.
Ableitung n-ter Ordnung nach der Variablen x der Funktion:
.
Formeln für Tangenten ableiten > > > ; für Kotangens > > >
Integrale
Serienerweiterungen
Um die Entwicklung des Tangens in Potenzen von x zu erhalten, müssen Sie mehrere Terme der Entwicklung in einer Potenzreihe für die Funktionen verwenden Sünde x Und weil x und dividiere diese Polynome durcheinander, . Dadurch ergeben sich die folgenden Formeln.
Bei .
bei .
Wo Mrd- Bernoulli-Zahlen. Sie werden entweder aus der Wiederholungsrelation bestimmt:
;
;
Wo .
Oder nach Laplaces Formel: 
Umkehrfunktionen
Die Umkehrfunktionen von Tangens und Kotangens sind Arkustangens bzw. Arkuskotangens.
Arcustangens, arctg
, Wo N- ganz.
Arkuskotangens, arcctg
, Wo N- ganz.
Verweise:
IN. Bronstein, K.A. Semendyaev, Handbuch der Mathematik für Ingenieure und Studenten, „Lan“, 2009.
G. Korn, Handbook of Mathematics for Scientists and Engineers, 2012.
In dem Artikel werden wir vollständig verstehen, wie es aussieht Tabelle der trigonometrischen Werte Sinus, Cosinus, Tangens und Kotangens. Betrachten wir die grundlegende Bedeutung trigonometrischer Funktionen aus einem Winkel von 0,30,45,60,90,...,360 Grad. Und sehen wir uns an, wie man diese Tabellen zur Berechnung der Werte trigonometrischer Funktionen verwendet.
Schauen wir uns zunächst an Tabelle mit Kosinus, Sinus, Tangens und Kotangens aus einem Winkel von 0, 30, 45, 60, 90,... Grad. Die Definition dieser Größen ermöglicht es uns, den Wert der Funktionen der Winkel von 0 und 90 Grad zu bestimmen:
sin 0 0 =0, cos 0 0 = 1. tg 00 = 0, Kotangens von 00 wird undefiniert sein
sin 90 0 = 1, cos 90 0 =0, ctg90 0 = 0, Tangente von 90 0 wird unsicher sein
Nehmen wir rechtwinklige Dreiecke mit einem Winkel von 30 bis 90 Grad. Wir bekommen:
sin 30 0 = 1/2, cos 30 0 = √3/2, tan 30 0 = √3/3, cos 30 0 = √3
sin 45 0 = √2/2, cos 45 0 = √2/2, tan 45 0 = 1, cos 45 0 = 1
sin 60 0 = √3/2, cos 60 0 = 1/2, tg 60 0 =√3, cot 60 0 = √3/3
Lassen Sie uns alle erhaltenen Werte im Formular darstellen trigonometrische Tabelle:
Tabelle mit Sinus, Cosinus, Tangens und Kotangens!
Wenn wir die Reduktionsformel verwenden, vergrößert sich unsere Tabelle und fügt Werte für Winkel bis zu 360 Grad hinzu. Es wird so aussehen:

Basierend auf den Eigenschaften der Periodizität kann die Tabelle auch erweitert werden, wenn wir die Winkel durch 0 0 +360 0 *z .... 330 0 +360 0 *z ersetzen, wobei z eine ganze Zahl ist. In dieser Tabelle ist es möglich, den Wert aller Winkel zu berechnen, die Punkten in einem einzelnen Kreis entsprechen.

Sehen wir uns an, wie die Tabelle in einer Lösung verwendet wird.
Alles ist sehr einfach. Da der von uns benötigte Wert am Schnittpunkt der von uns benötigten Zellen liegt. Nehmen wir zum Beispiel den Cos-Wert eines Winkels von 60 Grad. In der Tabelle sieht das so aus:

In der Abschlusstabelle der Hauptwerte trigonometrischer Funktionen gehen wir genauso vor. Aber in dieser Tabelle ist es möglich herauszufinden, wie groß die Tangente aus einem Winkel von 1020 Grad ist, nämlich = -√3. Schauen wir uns an: 1020 0 = 300 0 +360 0 *2. Finden wir es anhand der Tabelle.

Bradis-Tisch. Für Sinus, Cosinus, Tangens und Kotangens.
Die Bradis-Tabellen sind in mehrere Teile unterteilt, bestehend aus Tabellen für Kosinus und Sinus, Tangens und Kotangens, die in zwei Teile unterteilt sind (tg für Winkel bis zu 90 Grad und ctg für kleine Winkel).
Sinus und Cosinus


tg des Winkels beginnt bei 00 und endet mit 760, ctg des Winkels beginnt mit 140 und endet mit 900.
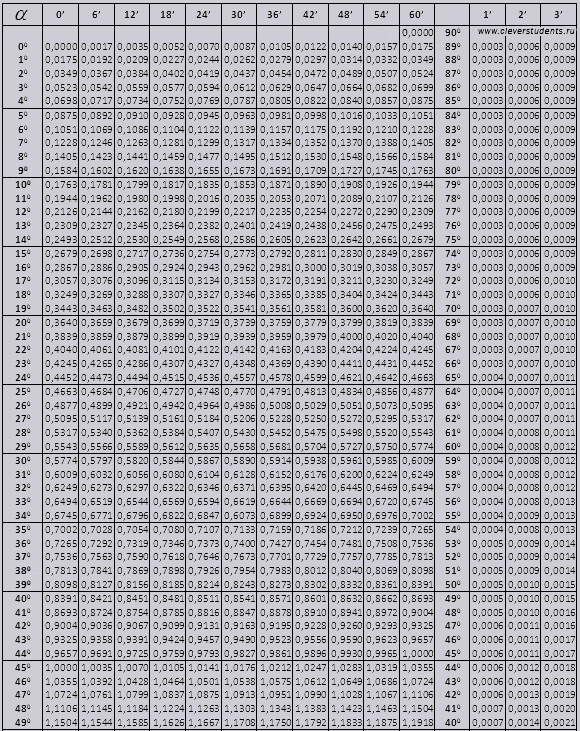

tg bis 900 und ctg von kleinen Winkeln.
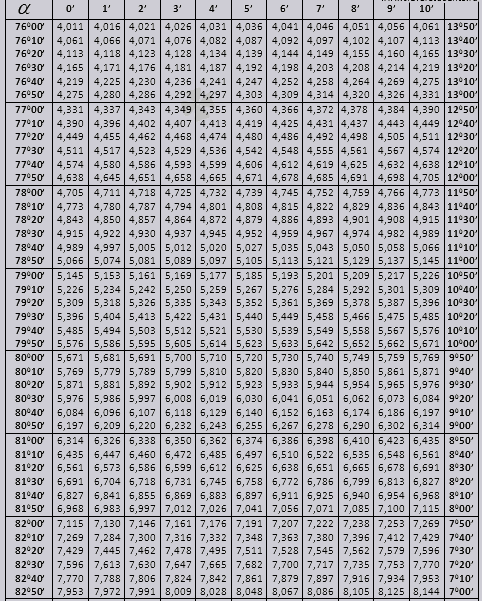
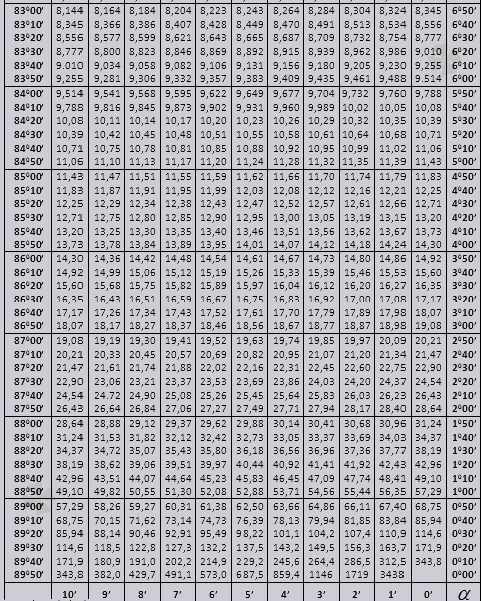
Lassen Sie uns herausfinden, wie Sie Bradis-Tabellen zur Lösung von Problemen verwenden können.
Finden wir die Bezeichnung sin (Bezeichnung in der Spalte am linken Rand) 42 Minuten (Bezeichnung steht in der oberen Zeile). Durch den Schnittpunkt suchen wir nach der Bezeichnung, it = 0,3040.
Die Minutenwerte werden im Abstand von sechs Minuten angegeben, was zu tun ist, wenn der von uns benötigte Wert genau in diesem Intervall liegt. Nehmen wir 44 Minuten, aber es sind nur 42 in der Tabelle. Wir nehmen 42 als Basis und verwenden die zusätzlichen Spalten auf der rechten Seite, nehmen den 2. Zusatz und addieren zu 0,3040 + 0,0006, wir erhalten 0,3046.
Bei sin 47 Minuten nehmen wir 48 Minuten als Basis und ziehen davon 1 Korrektur ab, also 0,3057 – 0,0003 = 0,3054
Bei der Berechnung von cos gehen wir ähnlich vor wie bei sin, nur nehmen wir die unterste Zeile der Tabelle als Grundlage. Zum Beispiel cos 20 0 = 0,9397
Die Werte für tg-Winkel bis 90 0 und cot eines kleinen Winkels sind korrekt und enthalten keine Korrekturen. Finden Sie beispielsweise tg 78 0 37min = 4,967 
und ctg 20 0 13min = 25,83 
Nun, wir haben uns die grundlegenden trigonometrischen Tabellen angesehen. Wir hoffen, dass diese Informationen für Sie äußerst nützlich waren. Wenn Sie Fragen zu den Tabellen haben, schreiben Sie diese unbedingt in die Kommentare!
Hinweis: Wandstoßstangen sind Stoßfängerbretter zum Schutz von Wänden. Folgen Sie dem Link rahmenlose Wandstoßstangen (http://www.spi-polymer.ru/otboyniki/) und erfahren Sie mehr.
1. Trigonometrische Funktionen sind Elementarfunktionen, deren Argument ist Ecke. Trigonometrische Funktionen beschreiben die Beziehungen zwischen Seiten und spitzen Winkeln in einem rechtwinkligen Dreieck. Die Einsatzgebiete trigonometrischer Funktionen sind äußerst vielfältig. Beispielsweise können beliebige periodische Prozesse als Summe trigonometrischer Funktionen (Fourier-Reihe) dargestellt werden. Diese Funktionen tauchen häufig bei der Lösung von Differential- und Funktionsgleichungen auf.
2. Zu den trigonometrischen Funktionen gehören die folgenden 6 Funktionen: Sinus, Kosinus, Tangente,Kotangens, Sekante Und Kosekans. Zu jeder dieser Funktionen gibt es eine inverse trigonometrische Funktion.
3. Es ist praktisch, die geometrische Definition trigonometrischer Funktionen mit einzuführen Einheitskreis. Die folgende Abbildung zeigt einen Kreis mit dem Radius r=1. Der Punkt M(x,y) ist auf dem Kreis markiert. Der Winkel zwischen dem Radiusvektor OM und der positiven Richtung der Ox-Achse ist gleich α.
4. Sinus Winkel α ist das Verhältnis der Ordinate y des Punktes M(x,y) zum Radius r:
sinα=y/r.
Da r=1 ist, ist der Sinus gleich der Ordinate des Punktes M(x,y).
5. Kosinus Winkel α ist das Verhältnis der Abszisse x des Punktes M(x,y) zum Radius r:
cosα=x/r
6. Tangente Winkel α ist das Verhältnis der Ordinate y eines Punktes M(x,y) zu seiner Abszisse x:
tanα=y/x,x≠0
7. Kotangens Winkel α ist das Verhältnis der Abszisse x eines Punktes M(x,y) zu seiner Ordinate y:
cotα=x/y,y≠0
8. Sekante Winkel α ist das Verhältnis des Radius r zur Abszisse x des Punktes M(x,y):
secα=r/x=1/x,x≠0
9. Kosekans Winkel α ist das Verhältnis des Radius r zur Ordinate y des Punktes M(x,y):
cscα=r/y=1/y,y≠0
10. Im Einheitskreis bilden die Projektionen x, y, die Punkte M(x,y) und der Radius r ein rechtwinkliges Dreieck, in dem x,y die Schenkel und r die Hypotenuse sind. Daher werden die obigen Definitionen trigonometrischer Funktionen, angewendet auf ein rechtwinkliges Dreieck, wie folgt formuliert:
Sinus Winkel α ist das Verhältnis der Gegenkathete zur Hypotenuse.
Kosinus Winkel α ist das Verhältnis des Nachbarschenkels zur Hypotenuse.
Tangente Der Winkel α wird als Gegenschenkel zum Nachbarschenkel bezeichnet.
Kotangens Der Winkel α wird als angrenzende Seite zur gegenüberliegenden Seite bezeichnet.
Sekante Winkel α ist das Verhältnis der Hypotenuse zum angrenzenden Schenkel.
Kosekans Winkel α ist das Verhältnis der Hypotenuse zum gegenüberliegenden Schenkel.
11. Diagramm der Sinusfunktion
y=sinx, Definitionsbereich: x∈R, Wertebereich: −1≤sinx≤1
12. Diagramm der Kosinusfunktion
y=cosx, Domäne: x∈R, Bereich: −1≤cosx≤1
13. Graph der Tangensfunktion 14. Diagramm der Kotangensfunktion 15. Graph der Sekantenfunktion
y=tanx, Definitionsbereich: x∈R,x≠(2k+1)π/2, Wertebereich: −∞ 
y=cotx, Definitionsbereich: x∈R,x≠kπ, Bereich: −∞ 
y=secx, Domäne: x∈R,x≠(2k+1)π/2, Bereich: secx∈(−∞,−1]∪∪)











