heim » Privates Haus » Polar Koordinaten. Kartesischen Koordinaten

Polar Koordinaten. Kartesischen Koordinaten

Ein rechtwinkliges Koordinatensystem auf einer Ebene wird durch zwei zueinander senkrechte Koordinatenachsen X’X und Y’Y gebildet. Die Koordinatenachsen schneiden sich im Punkt O, der als Ursprung bezeichnet wird. Auf jeder Achse wird eine positive Richtung ausgewählt. Die positive Richtung der Achsen (in einem rechtshändigen Koordinatensystem) wird so gewählt, dass beim Drehen der X-Achse die X-Achse gedreht wird um 90° gegen den Uhrzeigersinn, seine positive Richtung stimmt mit der positiven Richtung der Y'Y-Achse überein. Die vier Winkel (I, II, III, IV), die durch die Koordinatenachsen X'X und Y'Y gebildet werden, werden Koordinatenwinkel genannt (siehe Abb. 1).

Die Position des Punktes A auf der Ebene wird durch zwei Koordinaten x und y bestimmt. Die x-Koordinate entspricht der Länge des Segments OB, die y-Koordinate entspricht der Länge des Segments OC in den ausgewählten Maßeinheiten. Die Segmente OB und OC werden durch Linien definiert, die vom Punkt A parallel zur Y'Y- bzw. X'X-Achse gezogen werden. Die x-Koordinate heißt Abszisse von Punkt A, die y-Koordinate heißt Ordinate von Punkt A. Sie wird wie folgt geschrieben: A(x, y).

Liegt Punkt A im Koordinatenwinkel I, dann hat Punkt A eine positive Abszisse und Ordinate. Liegt Punkt A im Koordinatenwinkel II, dann hat Punkt A eine negative Abszisse und eine positive Ordinate. Liegt Punkt A im Koordinatenwinkel III, dann hat Punkt A eine negative Abszisse und Ordinate. Liegt Punkt A im Koordinatenwinkel IV, dann hat Punkt A eine positive Abszisse und eine negative Ordinate.

Rechteckiges Koordinatensystem im Raum wird durch drei zueinander senkrechte Koordinatenachsen OX, OY und OZ gebildet. Die Koordinatenachsen schneiden sich im Punkt O, der als Ursprung bezeichnet wird. Auf jeder Achse wird eine positive Richtung ausgewählt, die durch Pfeile angezeigt wird, und eine Maßeinheit für die Segmente auf den Achsen. Die Maßeinheiten sind für alle Achsen gleich. OX – Abszissenachse, OY – Ordinatenachse, OZ – Anwendungsachse. Die positive Richtung der Achsen ist so gewählt, dass bei einer Drehung der OX-Achse um 90° gegen den Uhrzeigersinn ihre positive Richtung mit der positiven Richtung der OY-Achse übereinstimmt, wenn diese Drehung aus der positiven Richtung der OZ-Achse betrachtet wird. Ein solches Koordinatensystem heißt rechtshändig. Nimmt man den Daumen der rechten Hand als X-Richtung, den Zeigefinger als Y-Richtung und den Mittelfinger als Z-Richtung, so entsteht ein rechtshändiges Koordinatensystem. Ähnliche Finger der linken Hand bilden das linke Koordinatensystem. Es ist unmöglich, das rechte und das linke Koordinatensystem so zu kombinieren, dass die entsprechenden Achsen zusammenfallen (siehe Abb. 2).

Die Position des Punktes A im Raum wird durch drei Koordinaten x, y und z bestimmt. Die x-Koordinate ist gleich der Länge des Segments OB, die y-Koordinate ist die Länge des Segments OC, die z-Koordinate ist die Länge des Segments OD in den ausgewählten Maßeinheiten. Die Segmente OB, OC und OD werden durch Ebenen definiert, die vom Punkt A parallel zu den Ebenen YOZ, XOZ bzw. XOY gezogen werden. Die x-Koordinate heißt Abszisse von Punkt A, die y-Koordinate heißt Ordinate von Punkt A, die z-Koordinate heißt Applikate von Punkt A. Sie wird wie folgt geschrieben: A(a, b, c).

Orty

Ein rechteckiges Koordinatensystem (beliebiger Dimension) wird auch durch eine Reihe von Einheitsvektoren beschrieben, die an den Koordinatenachsen ausgerichtet sind. Die Anzahl der Einheitsvektoren entspricht der Dimension des Koordinatensystems und sie stehen alle senkrecht zueinander.

Im dreidimensionalen Fall werden solche Einheitsvektoren üblicherweise bezeichnet ich J k oder e X e j e z. Dabei gelten bei einem rechtshändigen Koordinatensystem folgende Formeln mit dem Vektorprodukt von Vektoren:

[ich J]=k ;
[J k]=ich ;
[k ich]=J .

Geschichte

Das rechteckige Koordinatensystem wurde erstmals 1637 von Rene Descartes in seinem Werk „Diskurs über die Methode“ eingeführt. Daher wird das rechtwinklige Koordinatensystem auch genannt: Kartesisches Koordinatensystem. Die Koordinatenmethode zur Beschreibung geometrischer Objekte markierte den Beginn der analytischen Geometrie. Auch Pierre Fermat war an der Entwicklung der Koordinatenmethode beteiligt, seine Werke wurden jedoch erst nach seinem Tod veröffentlicht. Descartes und Fermat verwendeten die Koordinatenmethode nur auf der Ebene.

Die Koordinatenmethode für den dreidimensionalen Raum wurde bereits im 18. Jahrhundert von Leonhard Euler erstmals angewendet.

siehe auch

Links

Wikimedia-Stiftung. 2010.

Kartesisches Koordinatensystem
Kartesischer Grad

Sehen Sie, was „kartesische Koordinaten“ in anderen Wörterbüchern sind:

KARTESINKOORDINATEN- (Kartesisches Koordinatensystem) ein Koordinatensystem in einer Ebene oder im Raum, meist mit zueinander senkrechten Achsen und gleichen Maßstäben entlang der Achsen; rechtwinklige kartesische Koordinaten. Benannt nach R. Descartes... Großes enzyklopädisches Wörterbuch

Kartesischen Koordinaten- Ein Koordinatensystem bestehend aus zwei senkrechten Achsen. Die Position eines Punktes in einem solchen System wird anhand zweier Zahlen gebildet, die den Abstand vom Koordinatenmittelpunkt entlang jeder der Achsen bestimmen. Informationsthemen... ... Leitfaden für technische Übersetzer

Kartesischen Koordinaten- (Kartesisches Koordinatensystem), ein Koordinatensystem in einer Ebene oder im Raum, meist mit zueinander senkrechten Achsen und gleichen Maßstäben entlang der Achsen; rechtwinklige kartesische Koordinaten. Benannt nach R. Descartes... Enzyklopädisches Wörterbuch

Kartesischen Koordinaten- Dekarto koordinieren Statusas T sritis Standardizacija ir metrologija apibrėžtis Tiesinė plokštumos arba erdvės koordinačių sistema. Joje ašių masteliai paprastai būna lygūs. atitikmenys: engl. Kartesische Koordinaten vok. kartesische Koordinaten, f… Penkiakalbis aiškinamasis metrologijos terminų žodynas

Kartesischen Koordinaten- Dekarto koordinieren Statusas T sritis fizika atitikmenys: engl. Kartesischen Koordinaten; Gitterkoordinaten vok. kartesische Koordinaten, f rus. Kartesische Koordinaten, f pranc. coordonnées cartésiennes, f … Fizikos terminų žodynas

KARTESINKOORDINATEN- eine Methode zur Bestimmung der Position von Punkten auf einer Ebene anhand ihrer Abstände zu zwei festen senkrechten geraden Achsen. Dieses Konzept findet sich bereits bei Archimedes und Appologis von Perge vor mehr als zweitausend Jahren und sogar bei den alten Ägyptern. Zum ersten Mal... ... Mathematische Enzyklopädie

KARTESINKOORDINATEN- Kartesisches Koordinatensystem [benannt nach den Franzosen. Philosoph und Mathematiker R. Descartes (R. Descartes; 1596 1650)], ein Koordinatensystem in einer Ebene oder im Raum, meist mit zueinander senkrechten Achsen und gleichen Maßstäben entlang der Achsen rechteckig D ... Großes enzyklopädisches polytechnisches Wörterbuch

KARTESINKOORDINATEN- (kartesisches Koordinatensystem), ein Koordinatensystem in einer Ebene oder im Raum, meist mit zueinander senkrechten Achsen und gleichen Maßstäben entlang der rechtwinkligen Achsen. Benannt nach R. Descartes... Naturwissenschaft. Enzyklopädisches Wörterbuch

KARTESINKOORDINATEN- Das System zur Positionierung jedes auf den Knochen gefundenen Punktes relativ zu zwei Achsen, die sich im rechten Winkel schneiden. Dieses von René Descartes entwickelte System wurde zur Grundlage für Standardmethoden zur grafischen Darstellung von Daten. Horizontale Linie… … Erklärendes Wörterbuch der Psychologie

Koordinaten- Koordinaten. Im Flugzeug (links) und im Weltraum (rechts). KOORDINATEN (von lat. co zusammen und ordinatus geordnet), Zahlen, die die Position eines Punktes auf einer geraden Linie, Ebene, Fläche, im Raum bestimmen. Koordinaten sind Entfernungen... Illustriertes enzyklopädisches Wörterbuch

Polar Koordinaten

Die Nummer wird angerufen Polarradius Punkte bzw erste Polarkoordinate. Der Abstand kann nicht negativ sein, daher beträgt der Polarradius jedes Punktes. Die erste Polarkoordinate wird ebenfalls mit einem griechischen Buchstaben („rho“) bezeichnet, aber ich bin an die lateinische Version gewöhnt und werde sie in Zukunft verwenden.

Die Nummer wird angerufen Polarwinkel gegebener Punkt bzw zweite Polarkoordinate. Der Polarwinkel variiert typischerweise innerhalb (des sogenannten Hauptwinkelwerte). Es ist jedoch durchaus akzeptabel, den Bereich zu verwenden, und in einigen Fällen besteht die direkte Notwendigkeit, alle Winkelwerte von Null bis „plus Unendlich“ zu berücksichtigen. Übrigens empfehle ich, sich an das Bogenmaß eines Winkels zu gewöhnen, da die Arbeit mit Graden in der höheren Mathematik als nicht selbstverständlich gilt.

Das Paar wird aufgerufen Polar Koordinaten Punkte Es ist leicht, ihre spezifische Bedeutung zu finden. Der Tangens eines spitzen Winkels eines rechtwinkligen Dreiecks ist das Verhältnis der Gegenseite zur Nachbarseite: Daher ist der Winkel selbst: . Nach dem Satz des Pythagoras ist das Quadrat der Hypotenuse gleich der Summe der Quadrate der Schenkel: , was den Polarradius bedeutet:

Auf diese Weise, .

Ein Pinguin ist gut, aber ein Schwarm ist besser:

Negativ ausgerichtete Winkel Ich habe es vorsichtshalber mit Pfeilen markiert, für den Fall, dass einige Leser diese Ausrichtung noch nicht kannten. Wenn Sie möchten, können Sie an jedem von ihnen eine Umdrehung (rad. oder 360 Grad) „schrauben“ und es sich übrigens bequem machen Tabellenwerte:

Der Nachteil dieser „traditionell“ ausgerichteten Winkel besteht jedoch darin, dass sie zu weit (mehr als 180 Grad) gegen den Uhrzeigersinn „verdreht“ sind. Ich nehme die Frage vorweg: „Warum gibt es einen Nachteil und warum sind überhaupt einige negative Aspekte nötig?“ In der Mathematik werden die kürzesten und rationalsten Wege geschätzt. Nun, aus physikalischer Sicht ist die Drehrichtung oft von grundlegender Bedeutung – jeder von uns hat versucht, die Tür zu öffnen, indem er am Griff in die falsche Richtung zog =)

Die Reihenfolge und Technik der Punktkonstruktion in Polarkoordinaten

Schöne Bilder sind schön, aber sie in einem Polarkoordinatensystem zu konstruieren, ist eine ziemlich mühsame Aufgabe. Bei Punkten mit Polarwinkeln gibt es keine Schwierigkeiten , in unserem Beispiel sind das Punkte ; Auch Werte, die ein Vielfaches von 45 Grad sind, bereiten keine großen Probleme: . Aber wie konstruiert man beispielsweise einen Punkt richtig und kompetent?

Sie benötigen ein kariertes Blatt Papier, einen Bleistift und folgende Zeichenwerkzeuge: Lineal, Zirkel, Winkelmesser. Als letzten Ausweg können Sie mit nur einem Lineal auskommen oder sogar ... ganz ohne! Lesen Sie weiter und Sie werden einen weiteren Beweis dafür erhalten, dass dieses Land unbesiegbar ist =)

Beispiel 1

Konstruieren Sie einen Punkt im Polarkoordinatensystem.

Zunächst müssen Sie das Gradmaß des Winkels ermitteln. Wenn die Ecke unbekannt ist oder Sie Zweifel haben, ist es immer besser, sie zu verwenden Tisch oder eine allgemeine Formel zur Umrechnung von Bogenmaß in Grad. Unser Blickwinkel ist also (oder).

Zeichnen wir ein Polarkoordinatensystem (siehe Anfang der Lektion) und nehmen wir einen Winkelmesser zur Hand. Besitzer eines runden Instruments werden keine Schwierigkeiten haben, 240 Grad zu markieren, aber höchstwahrscheinlich haben Sie eine halbrunde Version des Geräts in Ihren Händen. Das Problem des völligen Fehlens eines Winkelmessers bei Vorhandensein eines Druckers und einer Schere durch Handarbeit gelöst.

Es gibt zwei Möglichkeiten: Drehen Sie das Blatt um und markieren Sie 120 Grad, oder „schrauben“ Sie eine halbe Umdrehung und betrachten Sie den entgegengesetzten Winkel. Wählen wir die Erwachsenenmethode und markieren Sie 60 Grad:

Entweder ein Liliput-Winkelmesser oder ein riesiger Käfig =) Um einen Winkel zu messen, ist der Maßstab jedoch nicht wichtig.

Zeichnen Sie mit einem Bleistift eine dünne gerade Linie durch die Stange und die Markierung:

Wir haben den Winkel geklärt, jetzt kommt als nächstes der Polradius. Nehmen Sie einen Kompass und entlang der Linie Wir setzen seine Lösung auf 3 Einheiten, am häufigsten sind das natürlich Zentimeter:

Nun setzen wir die Nadel vorsichtig auf die Stange und machen mit einer Drehbewegung eine kleine Kerbe (rote Farbe). Der benötigte Punkt wurde konstruiert:

Auf einen Zirkel können Sie verzichten, indem Sie das Lineal direkt an der konstruierten Geraden ansetzen und 3 Zentimeter abmessen. Aber wie wir später sehen werden, bei Problemen mit der Konstruktion in einem Polarkoordinatensystem Eine typische Situation besteht darin, dass Sie zwei oder mehr Punkte mit demselben Polarradius markieren müssen, um das Metall effizienter zu härten. Insbesondere in unserer Zeichnung ist es durch Drehen des Zirkelschenkels um 180 Grad einfach, eine zweite Kerbe zu machen und einen Punkt zu konstruieren, der relativ zur Stange symmetrisch ist. Lassen Sie uns damit den Stoff im nächsten Absatz durcharbeiten:

Beziehung zwischen rechtwinkligen und polaren Koordinatensystemen

Offensichtlich fügen wir hinzu Verknüpfen Sie das Polarkoordinatensystem mit einem „regulären“ Koordinatengitter und zeichnen Sie einen Punkt in der Zeichnung ein:

Es ist immer sinnvoll, diesen Zusammenhang beim Zeichnen in Polarkoordinaten im Hinterkopf zu behalten. Obwohl es sich wohl oder übel ohne weiteren Hinweis ergibt.

Stellen wir den Zusammenhang zwischen Polar- und kartesischen Koordinaten am Beispiel eines bestimmten Punktes her. Stellen Sie sich ein rechtwinkliges Dreieck vor, bei dem die Hypotenuse gleich dem Polarradius ist: und die Schenkel gleich den „X“- und „Y“-Koordinaten des Punktes im kartesischen Koordinatensystem sind: .

Der Sinus eines spitzen Winkels ist das Verhältnis der Gegenkathete zur Hypotenuse:

Der Kosinus eines spitzen Winkels ist das Verhältnis des angrenzenden Schenkels zur Hypotenuse:

Gleichzeitig wiederholten wir die Definitionen von Sinus, Cosinus (und etwas früher Tangens) aus dem Lehrplan der 9. Klasse einer Gesamtschule.

Bitte fügen Sie Ihrem Nachschlagewerk Arbeitsformeln hinzu, die die kartesischen Koordinaten eines Punktes durch seine Polarkoordinaten ausdrücken – wir werden uns mehr als einmal damit befassen müssen, und das nächste Mal gleich jetzt =)

Finden wir die Koordinaten eines Punktes in einem rechteckigen Koordinatensystem:

Auf diese Weise:

Die resultierenden Formeln öffnen eine weitere Lücke im Konstruktionsproblem, wenn man auf einen Winkelmesser überhaupt verzichten kann: Zuerst finden wir die kartesischen Koordinaten des Punktes (natürlich im Entwurf), dann finden wir gedanklich die gewünschte Stelle auf der Zeichnung und Markieren Sie diesen Punkt. Im letzten Schritt zeichnen wir eine dünne gerade Linie, die durch den konstruierten Punkt und den Pol verläuft. Dabei stellt sich heraus, dass der Winkel angeblich mit einem Winkelmesser gemessen wurde.

Witzig ist, dass sehr verzweifelte Schüler sogar auf ein Lineal verzichten und stattdessen die glatte Kante eines Lehrbuchs, Notizbuchs oder Notenbuchs verwenden können – schließlich haben sich die Notebook-Hersteller um die Maße gekümmert, 1 Quadrat = 5 Millimeter.

Das alles erinnerte mich an einen bekannten Witz, in dem findige Piloten einen Kurs entlang eines Rudels von Belomor planten =) Auch wenn der Witz, Spaß beiseite, nicht so weit von der Realität entfernt ist, erinnere ich mich an einen der Inlandsflüge in Russland Federation, alle Navigationsinstrumente im Flugzeug versagten und die Besatzung erfolgreich landete. Ich habe das Flugzeug mit einem normalen Glas Wasser gelandet, das den Winkel des Flugzeugs relativ zum Boden anzeigte. Und die Landebahn – hier ist sie, von der Windschutzscheibe aus sichtbar.

Mit dem zu Beginn der Lektion zitierten Satz des Pythagoras lassen sich leicht die Umkehrformeln erhalten: , also:

Der Winkel „Phi“ selbst wird standardmäßig durch den Arkustangens ausgedrückt – absolut dasselbe wie komplexes Zahlenargument mit all seinen Problemen.

Es empfiehlt sich auch, die zweite Formelgruppe in Ihr Referenzgepäck aufzunehmen.

Kommen wir nach einer ausführlichen Nachbesprechung der einzelnen Punkte zur natürlichen Fortsetzung des Themas:

Gleichung einer Geraden in Polarkoordinaten

Im Wesentlichen lautet die Gleichung einer Geraden in einem Polarkoordinatensystem Funktion des Polarradius vom Polarwinkel (Argument). In diesem Fall wird der Polarwinkel berücksichtigt im Bogenmaß(!) Und ständig nimmt Werte von bis an (Manchmal sollte es bis ins Unendliche betrachtet werden, oder in einer Reihe von Problemen der Einfachheit halber von bis). Jeder Wert des Winkels „Phi“, der darin enthalten ist Domain Funktion, entspricht einem einzelnen Wert des Polarradius.

Die Polarfunktion kann mit einer Art Radar verglichen werden – wenn sich ein von einem Pol ausgehender Lichtstrahl gegen den Uhrzeigersinn dreht und eine Linie „erkennt“ (zeichnet).

Ein Standardbeispiel für eine Polarkurve ist Archimedische Spirale. Das folgende Bild zeigt sie erste Runde– wenn der dem Polarwinkel folgende Polarradius Werte von 0 bis annimmt:

Wenn die Spirale die Polachse am Punkt kreuzt, wird sie sich weiter entfalten und sich unendlich weit vom Pol entfernen. In der Praxis kommen solche Fälle jedoch eher selten vor; Eine typischere Situation ist, dass wir bei allen nachfolgenden Umdrehungen „auf derselben Linie gehen“, die im Bereich erhalten wurde.

Im ersten Beispiel stoßen wir auf das Konzept Definitionsbereich Polarfunktion: Da der Polarradius nicht negativ ist, können negative Winkel hier nicht berücksichtigt werden.

! Notiz : In einigen Fällen ist die Verwendung üblich verallgemeinerte Polarkoordinaten, wobei der Radius negativ sein kann, und wir werden diesen Ansatz etwas später kurz untersuchen

Neben der Archimedes-Spirale gibt es noch viele andere berühmte Kurven, aber wie man so schön sagt, von Kunst kann man nicht genug bekommen, deshalb habe ich Beispiele ausgewählt, die sehr oft in realen praktischen Aufgaben zu finden sind.

Zunächst die einfachsten Gleichungen und einfachsten Linien:

Eine Gleichung der Form gibt diejenige an, die vom Pol ausgeht Strahl. Denken Sie in der Tat darüber nach, ob der Winkelwert Stets(was auch immer das „er“ ist) ständig, welche Zeile ist es dann?

Notiz : Im verallgemeinerten Polarkoordinatensystem definiert diese Gleichung eine gerade Linie, die durch den Pol verläuft

Eine Gleichung der Form bestimmt... beim ersten Mal raten - wenn für jeden Winkel „Phi“-Radius bleibt konstant? Tatsächlich ist dies die Definition Kreis zentriert am Pol des Radius.

Zum Beispiel, . Der Übersichtlichkeit halber finden wir die Gleichung dieser Geraden in einem rechtwinkligen Koordinatensystem. Unter Verwendung der im vorherigen Absatz erhaltenen Formel führen wir die Ersetzung durch:

Quadrieren wir beide Seiten:

– Gleichung eines Kreises mit Mittelpunkt im Ursprung von Radius 2, was überprüft werden musste.

Seit der Erstellung und Veröffentlichung des Artikels über lineare Abhängigkeit und lineare Unabhängigkeit von Vektoren Ich habe mehrere Briefe von Website-Besuchern erhalten, die eine Frage im Sinne von „Es gibt ein einfaches und praktisches rechteckiges Koordinatensystem, warum brauchen wir einen weiteren schrägen affinen Fall?“ haben. Die Antwort ist einfach: Die Mathematik strebt danach, alles und jeden zu umfassen! Darüber hinaus ist in einer bestimmten Situation die Bequemlichkeit wichtig – wie Sie sehen, ist es aufgrund der extremen Einfachheit der Gleichung viel rentabler, mit einem Kreis in Polarkoordinaten zu arbeiten.

Und manchmal nimmt ein mathematisches Modell wissenschaftliche Entdeckungen vorweg. So war einst der Rektor der Kasaner Universität N.I. Lobatschewski streng bewiesen, durch einen beliebigen Punkt der Ebene kann man zeichnen unendlich viele Geraden, parallel zu diesem. Infolgedessen wurde er von der gesamten wissenschaftlichen Welt diffamiert, aber... niemand konnte diese Tatsache widerlegen. Nur ein gutes Jahrhundert später entdeckten Astronomen, dass sich Licht im Weltraum auf gekrümmten Bahnen bewegt, wobei Lobatschewskis nichteuklidische Geometrie, die er lange vor dieser Entdeckung formal entwickelt hatte, zu funktionieren beginnt. Es wird angenommen, dass es sich dabei um eine Eigenschaft des Raumes selbst handelt, dessen Krümmung aufgrund der (nach astronomischen Maßstäben) geringen Entfernung für uns unsichtbar ist.

Betrachten wir sinnvollere Bauaufgaben:

Beispiel 2

Bilden Sie eine Linie

Lösung: Lassen Sie uns zunächst herausfinden Domain. Da der Polarradius nicht negativ ist, muss die Ungleichung gelten. Sie können sich an die Schulregeln zum Lösen trigonometrischer Ungleichungen erinnern, aber in einfachen Fällen wie diesem empfehle ich eine schnellere und anschaulichere Lösungsmethode:

Stellen Sie sich einen Kosinusgraphen vor. Wenn es sich noch nicht in Ihrem Gedächtnis registriert hat, finden Sie es auf der Seite Graphen elementarer Funktionen. Was sagt uns Ungleichheit? Es sagt uns, dass der Kosinusgraph lokalisiert werden sollte nicht weniger Abszissenachse. Und das passiert auf dem Segment. Und dementsprechend ist das Intervall nicht geeignet.

Somit ist der Definitionsbereich unserer Funktion: , das heißt, der Graph befindet sich rechts vom Pol (in der Terminologie des kartesischen Systems - in der rechten Halbebene).

In Polarkoordinaten gibt es oft eine vage Vorstellung davon, welche Gerade eine bestimmte Gleichung definiert. Um sie also zu konstruieren, müssen Sie die dazugehörenden Punkte finden – und je mehr, desto besser. Normalerweise sind sie auf ein Dutzend oder zwei (oder sogar weniger) begrenzt. Der einfachste Weg ist natürlich die Einnahme Tischwinkelwerte. Zur besseren Übersicht werde ich eine Umdrehung auf negative Werte „schrauben“:

Aufgrund der Parität des Kosinus die entsprechenden positiven Werte müssen nicht erneut gezählt werden:

Lassen Sie uns ein Polarkoordinatensystem darstellen und die gefundenen Punkte grafisch darstellen, während es praktisch ist, die gleichen „er“-Werte gleichzeitig zu zeichnen, indem wir mit einem Kompass unter Verwendung der oben beschriebenen Technologie gepaarte Kerben erstellen:

Im Prinzip ist die Linie klar gezeichnet, aber um die Vermutung vollständig zu bestätigen, suchen wir ihre Gleichung im kartesischen Koordinatensystem. Sie können die kürzlich abgeleiteten Formeln anwenden , aber ich werde Ihnen von einem listigeren Trick erzählen. Wir multiplizieren beide Seiten der Gleichung künstlich mit „er“: und verwenden kompaktere Übergangsformeln:

Indem wir ein vollständiges Quadrat auswählen, bringen wir die Geradengleichung in eine erkennbare Form:

– Gleichung eines Kreises mit Mittelpunkt im Punkt , Radius 2.

Da es je nach Bedingung einfach notwendig war, die Konstruktion durchzuführen und das war's, verbinden wir die gefundenen Punkte reibungslos mit einer Linie:

Bereit. Es ist in Ordnung, wenn es etwas uneben wird, man musste nicht wissen, dass es ein Kreis ist ;-)

Warum haben wir die Winkelwerte außerhalb des Intervalls nicht berücksichtigt? Die Antwort ist einfach: Es hat keinen Sinn. Aufgrund der Periodizität der Funktion haben wir es mit einem endlosen Lauf entlang des konstruierten Kreises zu tun.

Es ist leicht, eine einfache Analyse durchzuführen und zu dem Schluss zu kommen, dass eine Gleichung der Form einen Kreis mit einem Durchmesser und einem Mittelpunkt im Punkt angibt. Im übertragenen Sinne „sitzen“ alle diese Kreise auf der Polachse und gehen zwangsläufig durch den Pol. Wenn jedoch, dann wird sich die fröhliche Gesellschaft nach links bewegen – zur Fortsetzung der Polarachse (überlegen Sie, warum).

Eine ähnliche Aufgabe zum Selbstlösen:

Beispiel 3

Konstruieren Sie eine Gerade und finden Sie ihre Gleichung in einem rechtwinkligen Koordinatensystem.

Lassen Sie uns das Vorgehen zur Lösung des Problems systematisieren:

Zunächst finden wir den Definitionsbereich der Funktion; hierfür ist es zweckmäßig, ihn zu betrachten Sinusoid um sofort zu verstehen, wo der Sinus nicht negativ ist.

Im zweiten Schritt berechnen wir die Polarkoordinaten der Punkte anhand Tischwinkelwerte; Analysieren Sie, ob es möglich ist, die Anzahl der Berechnungen zu reduzieren?

Im dritten Schritt tragen wir die Punkte im Polarkoordinatensystem ein und verbinden sie sorgfältig mit einer Linie.

Und schließlich finden wir die Geradengleichung im kartesischen Koordinatensystem.

Eine Beispiellösung finden Sie am Ende der Lektion.

Wir beschreiben den allgemeinen Algorithmus und die Konstruktionstechnik in Polarkoordinaten
und erheblich beschleunigen im zweiten Teil der Vorlesung, aber vorher lernen wir noch eine weitere gemeinsame Linie kennen:

Polarrose

Das ist richtig, wir sprechen von einer Blume mit Blütenblättern:

Beispiel 4

Konstruieren Sie Linien, die durch Gleichungen in Polarkoordinaten gegeben sind

Es gibt zwei Ansätze zur Konstruktion einer Polarrose. Folgen wir zunächst der gerändelten Spur unter der Annahme, dass der Polradius nicht negativ sein kann:

Lösung:

a) Finden wir den Definitionsbereich der Funktion:

Diese trigonometrische Ungleichung lässt sich auch grafisch leicht lösen: aus den Materialien des Artikels Geometrische Transformationen von Graphen Es ist bekannt, dass, wenn das Argument einer Funktion verdoppelt wird, ihr Graph um das Zweifache auf die Ordinatenachse schrumpft. Den Graphen der Funktion finden Sie im ersten Beispiel dieser Lektion. Wo liegt diese Sinuskurve oberhalb der x-Achse? In Intervallen . Folglich wird die Ungleichung durch die entsprechenden Segmente erfüllt, und Domain Unsere Funktion: .

Im Allgemeinen ist die Lösung der betrachteten Ungleichungen eine Vereinigung unendlich vieler Segmente, aber auch hier interessiert uns nur eine Periode.

Vielleicht fällt es einigen Lesern leichter, eine analytische Methode zur Ermittlung des Definitionsbereichs zu verwenden; ich nenne es „einen runden Kuchen in Scheiben schneiden“. Wir werden schneiden in gleiche Teile aufteilen und finden Sie zunächst die Grenzen des ersten Stücks. Wir argumentieren wie folgt: Sinus ist nicht negativ, Wann sein Argument reicht von 0 bis rad. inklusive. In unserem Beispiel: . Wenn wir alle Teile der doppelten Ungleichung durch 2 dividieren, erhalten wir das erforderliche Intervall:

Jetzt beginnen wir, nacheinander „gleiche 90-Grad-Stücke“ gegen den Uhrzeigersinn zu schneiden:

– Das gefundene Segment ist selbstverständlich im Definitionsbereich enthalten;

– nächstes Intervall – nicht enthalten;

– nächstes Segment – enthalten;

– und schließlich das Intervall – ist nicht enthalten.

Genau wie ein Gänseblümchen – „liebt, liebt nicht, liebt, liebt nicht“ =) Mit dem Unterschied, dass es hier keine Wahrsagerei gibt. Ja, es ist nur eine Art Liebe auf chinesische Art….

Also, und die Linie stellt eine Rose mit zwei identischen Blütenblättern dar. Es ist durchaus akzeptabel, die Zeichnung schematisch zu zeichnen, es wird jedoch dringend empfohlen, sie richtig zu finden und zu markieren Spitzen der Blütenblätter. Die Eckpunkte entsprechen Mittelpunkte von Segmenten des Definitionsbereichs, die in diesem Beispiel offensichtliche Winkelkoordinaten haben . Dabei Blütenblattlängen Sind:

Hier ist das natürliche Ergebnis eines fürsorglichen Gärtners:

Es ist zu beachten, dass die Länge des Blütenblatts leicht aus der Gleichung ersichtlich ist – da der Sinus begrenzt ist: , dann wird der Maximalwert von „er“ sicherlich zwei nicht überschreiten.

b) Konstruieren wir die durch die Gleichung gegebene Gerade. Offensichtlich beträgt die Länge des Blütenblatts dieser Rose auch zwei, aber zunächst einmal interessiert uns der Bereich der Definition. Wenden wir die analytische „Slicing“-Methode an: Sinus ist nicht negativ, wenn sein Argument vorliegt liegt im Bereich von Null bis einschließlich „pi“, in diesem Fall: . Wir dividieren alle Teile der Ungleichung durch 3 und erhalten das erste Intervall:

Als nächstes beginnen wir mit dem Rad, „den Kuchen in Stücke zu schneiden“. (60 Grad):
– Das Segment wird in den Definitionsbereich aufgenommen.
– Intervall – wird nicht berücksichtigt;
– Segment – wird passen;
– Intervall – wird nicht berücksichtigt;
– Segment – wird passen;
– Intervall – wird nicht berücksichtigt.

Der Prozess wird bei 360 Grad erfolgreich abgeschlossen.

Somit ist der Definitionsbereich: .

Die ganz oder teilweise ausgeführten Handlungen sind gedanklich leicht umzusetzen.

Konstruktion. Wenn im vorherigen Absatz mit rechten Winkeln und Winkeln von 45 Grad alles gut geklappt hat, dann müssen Sie hier ein wenig basteln. Lass uns finden Spitzen der Blütenblätter. Ihre Länge war von Beginn der Aufgabe an sichtbar, es müssen nur noch die Winkelkoordinaten berechnet werden, die den Mittelpunkten der Segmente des Definitionsbereichs entsprechen:

Bitte beachten Sie, dass zwischen den Spitzen der Blütenblätter gleiche Abstände vorhanden sein müssen, in diesem Fall 120 Grad.

Es empfiehlt sich, die Zeichnung in 60-Grad-Sektoren zu unterteilen (durch grüne Linien abgegrenzt) und die Richtungen der Spitzen der Blütenblätter einzuzeichnen (graue Linien). Es ist praktisch, die Scheitelpunkte selbst mit einem Zirkel zu markieren – messen Sie einmal einen Abstand von 2 Einheiten und machen Sie drei Kerben in den gezeichneten Richtungen von 30, 150 und 270 Grad:

Bereit. Ich verstehe, dass dies eine mühsame Aufgabe ist, aber wenn Sie alles mit Bedacht arrangieren wollen, müssen Sie Zeit investieren.

Lassen Sie uns eine allgemeine Formel formulieren: eine Gleichung der Form , ist eine natürliche Zahl) definiert eine polarblättrige Rose, deren Blütenblattlänge gleich ist.

Beispielsweise spezifiziert die Gleichung einen Vierpass mit einer Blütenblattlänge von 5 Einheiten, die Gleichung spezifiziert eine 5-blättrige Rose mit einer Blütenblattlänge von 3 Einheiten. usw.

Anweisungen

Schreiben Sie mathematische Operationen in Textform auf und geben Sie diese in das Suchabfragefeld auf der Hauptseite der Google-Website ein, wenn Sie keinen Taschenrechner verwenden können, aber Zugang zum Internet haben. Diese Suchmaschine verfügt über einen integrierten Multifunktionsrechner, der viel einfacher zu verwenden ist als alle anderen. Es gibt keine Schnittstelle mit Schaltflächen – alle Daten müssen in Textform in ein einziges Feld eingegeben werden. Zum Beispiel, wenn bekannt Koordinaten Extrempunkte Segment in einem dreidimensionalen Koordinatensystem A(51,34 17,2 13,02) und A(-11,82 7,46 33,5), dann Koordinaten Mittelpunkt Segment C((51,34-11,82)/2 (17,2+7,46)/2 (13,02+33,5)/2). Durch Eingabe von (51,34-11,82)/2 in das Suchabfragefeld, dann (17,2+7,46)/2 und (13,02+33,5)/2 können Sie Google verwenden, um Folgendes zu erhalten Koordinaten C(19,76 12,33 23,26).

Mit der Standardgleichung eines Kreises können Sie mehrere wichtige Informationen über diese Figur herausfinden, beispielsweise die Koordinaten ihres Mittelpunkts und die Länge des Radius. Bei einigen Problemen hingegen müssen Sie eine Gleichung unter Verwendung gegebener Parameter erstellen.

Anweisungen

Bestimmen Sie anhand der Ihnen gestellten Aufgabe, welche Informationen Sie über den Kreis haben. Denken Sie daran, dass das ultimative Ziel darin besteht, sowohl die Koordinaten des Mittelpunkts als auch den Durchmesser zu bestimmen. Alle Ihre Handlungen sollten darauf ausgerichtet sein, dieses besondere Ergebnis zu erreichen.

Verwenden Sie Daten zum Vorhandensein von Schnittpunkten mit Koordinatenlinien oder anderen Linien. Bitte beachten Sie, dass, wenn der Kreis durch die Abszissenachse verläuft, der zweite die Koordinate 0 hat, und wenn er durch die Ordinatenachse verläuft, dann der erste. Mithilfe dieser Koordinaten können Sie die Koordinaten des Kreismittelpunkts ermitteln und auch den Radius berechnen.

Vergessen Sie nicht die grundlegenden Eigenschaften von Sekanten und Tangenten. Der nützlichste Satz ist insbesondere, dass Radius und Tangente am Berührungspunkt einen rechten Winkel bilden. Bitte beachten Sie jedoch, dass Sie möglicherweise aufgefordert werden, alle im Kurs verwendeten Theoreme zu beweisen.

Lösen Sie die gängigsten Typen, um zu lernen, wie Sie bestimmte Daten für die Kreisgleichung verwenden. Zusätzlich zu den bereits erwähnten Problemen mit direkt gegebenen Koordinaten und denen, bei denen Informationen über das Vorhandensein von Schnittpunkten gegeben werden, können Sie zur Erstellung der Kreisgleichung Kenntnisse über den Mittelpunkt des Kreises und die Länge des Kreises verwenden Akkord und auf dem dieser Akkord liegt.

Konstruieren Sie zur Lösung ein gleichschenkliges Dreieck, dessen Basis die gegebene Sehne ist und dessen gleiche Seiten die Radien sind. Stellen Sie eine Datei zusammen, aus der Sie die erforderlichen Daten leicht finden können. Dazu reicht es aus, die Formel zum Ermitteln der Länge eines Segments in einer Ebene zu verwenden.

Video zum Thema

Unter einem Kreis versteht man eine Figur, die aus vielen Punkten auf einer Ebene mit gleichem Abstand von ihrem Mittelpunkt besteht. Abstand vom Mittelpunkt zu den Punkten Kreis Radius genannt.

Man nennt ein geordnetes System aus zwei oder drei sich schneidenden Achsen senkrecht zueinander mit einem gemeinsamen Ursprung (Koordinatenursprung) und einer gemeinsamen Längeneinheit rechteckiges kartesisches Koordinatensystem .

Allgemeines kartesisches Koordinatensystem (affines Koordinatensystem) müssen nicht unbedingt senkrechte Achsen enthalten. Zu Ehren des französischen Mathematikers René Descartes (1596–1662) wird ein solches Koordinatensystem benannt, bei dem auf allen Achsen eine gemeinsame Längeneinheit gemessen wird und die Achsen gerade sind.

Rechteckiges kartesisches Koordinatensystem auf einer Ebene hat zwei Achsen und rechteckiges kartesisches Koordinatensystem im Raum - drei Achsen. Jeder Punkt auf einer Ebene oder im Raum wird durch einen geordneten Satz von Koordinaten definiert – Zahlen, die der Längeneinheit des Koordinatensystems entsprechen.

Beachten Sie, dass sich, wie aus der Definition hervorgeht, ein kartesisches Koordinatensystem auf einer Geraden, also in einer Dimension, befindet. Die Einführung kartesischer Koordinaten auf einer Linie ist eine der Möglichkeiten, jeden Punkt auf einer Linie einer wohldefinierten reellen Zahl, also einer Koordinate, zuzuordnen.

Die Koordinatenmethode, die in den Werken von Rene Descartes entstand, markierte eine revolutionäre Umstrukturierung der gesamten Mathematik. Es wurde möglich, algebraische Gleichungen (oder Ungleichungen) in Form von geometrischen Bildern (Graphen) zu interpretieren und umgekehrt mithilfe analytischer Formeln und Gleichungssysteme nach Lösungen für geometrische Probleme zu suchen. Ja, Ungleichheit z < 3 геометрически означает полупространство, лежащее ниже плоскости, параллельной координатной плоскости xOy und liegt 3 Einheiten über dieser Ebene.

Unter Verwendung des kartesischen Koordinatensystems entspricht die Zugehörigkeit eines Punktes auf einer bestimmten Kurve der Tatsache, dass die Zahlen vorliegen X Und j eine Gleichung erfüllen. Somit sind die Koordinaten eines Punktes auf einem Kreis mit einem Mittelpunkt an einem bestimmten Punkt ( A; B) erfüllen die Gleichung (X - A)² + ( j - B)² = R² .

Rechteckiges kartesisches Koordinatensystem auf einer Ebene

Zwei senkrechte Achsen auf einer Ebene mit gemeinsamem Ursprung und gleicher Maßeinheitsform Kartesisches rechtwinkliges Koordinatensystem in der Ebene . Eine dieser Achsen wird Achse genannt Ochse, oder x-Achse , der andere - die Achse Oy, oder y-Achse . Diese Achsen werden auch Koordinatenachsen genannt. Bezeichnen wir mit MX Und Mj bzw. die Projektion eines beliebigen Punktes M auf der Achse Ochse Und Oy. Wie bekomme ich Prognosen? Lassen Sie uns den Punkt durchgehen M Ochse. Diese Gerade schneidet die Achse Ochse am Punkt MX. Lassen Sie uns den Punkt durchgehen M gerade Linie senkrecht zur Achse Oy. Diese Gerade schneidet die Achse Oy am Punkt Mj. Dies ist im Bild unten dargestellt.

X Und j Punkte M Wir nennen die Werte der gerichteten Segmente entsprechend OMX Und OMj. Die Werte dieser gerichteten Segmente werden entsprechend berechnet als X = X0 - 0 Und j = j0 - 0 . Kartesischen Koordinaten X Und j Punkte M Abszisse Und Ordinate . Die Tatsache, dass der Punkt M hat Koordinaten X Und j wird wie folgt bezeichnet: M(X, j) .

Koordinatenachsen teilen die Ebene in vier Teile Quadrant , deren Nummerierung in der folgenden Abbildung dargestellt ist. Es zeigt auch die Anordnung der Zeichen für die Koordinaten von Punkten in Abhängigkeit von ihrer Position in einem bestimmten Quadranten.

Neben kartesischen rechtwinkligen Koordinaten in einer Ebene wird häufig auch das Polarkoordinatensystem berücksichtigt. Über die Methode des Übergangs von einem Koordinatensystem zum anderen - in der Lektion Polarkoordinatensystem .

Rechteckiges kartesisches Koordinatensystem im Raum

Kartesische Koordinaten im Raum werden in völliger Analogie zu kartesischen Koordinaten in der Ebene eingeführt.

Drei zueinander senkrechte Achsen im Raum (Koordinatenachsen) mit einem gemeinsamen Ursprung Ö und mit der gleichen Skaleneinheit bilden sie sich Kartesisches rechtwinkliges Koordinatensystem im Raum .

Eine dieser Achsen wird Achse genannt Ochse, oder x-Achse , der andere - die Achse Oy, oder y-Achse , die dritte - Achse Oz, oder Achse anwenden . Lassen MX, Mj Mz- Projektionen eines beliebigen Punktes M Platz auf der Achse Ochse , Oy Und Oz jeweils.

Lassen Sie uns den Punkt durchgehen M OchseOchse am Punkt MX. Lassen Sie uns den Punkt durchgehen M Ebene senkrecht zur Achse Oy. Diese Ebene schneidet die Achse Oy am Punkt Mj. Lassen Sie uns den Punkt durchgehen M Ebene senkrecht zur Achse Oz. Diese Ebene schneidet die Achse Oz am Punkt Mz.

Kartesische rechtwinklige Koordinaten X , j Und z Punkte M Wir nennen die Werte der gerichteten Segmente entsprechend OMX, OMj Und OMz. Die Werte dieser gerichteten Segmente werden entsprechend berechnet als X = X0 - 0 , j = j0 - 0 Und z = z0 - 0 .

Kartesischen Koordinaten X , j Und z Punkte M heißen entsprechend Abszisse , Ordinate Und anwenden .

Paarweise aufgenommene Koordinatenachsen liegen in Koordinatenebenen xOy , yOz Und zOx .

Probleme über Punkte in einem kartesischen Koordinatensystem

Beispiel 1.

A(2; -3) ;

B(3; -1) ;

C(-5; 1) .

Finden Sie die Koordinaten der Projektionen dieser Punkte auf die Abszissenachse.

Lösung. Wie aus dem theoretischen Teil dieser Lektion hervorgeht, liegt die Projektion eines Punktes auf die Abszissenachse auf der Abszissenachse selbst, also der Achse Ochse und hat daher eine Abszisse, die der Abszisse des Punktes selbst entspricht, und eine Ordinate (Koordinate auf der Achse). Oy, den die x-Achse im Punkt 0 schneidet), der gleich Null ist. Wir erhalten also die folgenden Koordinaten dieser Punkte auf der x-Achse:

Ax(2;0);

Bx(3;0);

Cx (-5; 0).

Beispiel 2. Im kartesischen Koordinatensystem werden Punkte auf der Ebene angegeben

A(-3; 2) ;

B(-5; 1) ;

C(3; -2) .

Finden Sie die Koordinaten der Projektionen dieser Punkte auf die Ordinatenachse.

Lösung. Wie aus dem theoretischen Teil dieser Lektion hervorgeht, befindet sich die Projektion eines Punktes auf die Ordinatenachse auf der Ordinatenachse selbst, also der Achse Oy und hat daher eine Ordinate, die der Ordinate des Punktes selbst entspricht, und eine Abszisse (Koordinate auf der Achse). Ochse, den die Ordinatenachse im Punkt 0 schneidet), der gleich Null ist. Wir erhalten also die folgenden Koordinaten dieser Punkte auf der Ordinatenachse:

Ay(0;2);

By(0;1);

Cy(0;-2).

Beispiel 3. Im kartesischen Koordinatensystem werden Punkte auf der Ebene angegeben

A(2; 3) ;

B(-3; 2) ;

C(-1; -1) .

Ochse .

Ochse Ochse Ochse hat die gleiche Abszisse wie der gegebene Punkt und eine Ordinate, deren Absolutwert der Ordinate des gegebenen Punktes entspricht und deren Vorzeichen entgegengesetzt ist. Wir erhalten also die folgenden Koordinaten von Punkten, die relativ zur Achse symmetrisch zu diesen Punkten sind Ochse :

A"(2; -3) ;

B"(-3; -2) ;

C"(-1; 1) .

Lösen Sie selbst Probleme mit dem kartesischen Koordinatensystem und schauen Sie sich dann die Lösungen an

Beispiel 4. Bestimmen Sie, in welchen Quadranten (Viertel, Zeichnung mit Quadranten – am Ende des Absatzes „Rechteckiges kartesisches Koordinatensystem in einer Ebene“) ein Punkt liegen kann M(X; j) , Wenn

1) xy > 0 ;

2) xy < 0 ;

3) X − j = 0 ;

4) X + j = 0 ;

5) X + j > 0 ;

6) X + j < 0 ;

7) X − j > 0 ;

8) X − j < 0 .

Beispiel 5. Im kartesischen Koordinatensystem werden Punkte auf der Ebene angegeben

A(-2; 5) ;

B(3; -5) ;

C(A; B) .

Finden Sie die Koordinaten von Punkten, die relativ zur Achse symmetrisch zu diesen Punkten sind Oy .

Lassen Sie uns weiterhin gemeinsam Probleme lösen

Beispiel 6. Im kartesischen Koordinatensystem werden Punkte auf der Ebene angegeben

A(-1; 2) ;

B(3; -1) ;

C(-2; -2) .

Finden Sie die Koordinaten von Punkten, die relativ zur Achse symmetrisch zu diesen Punkten sind Oy .

Lösung. 180 Grad um die Achse drehen Oy Richtungssegment von der Achse Oy Bis hierhin. In der Abbildung, in der die Quadranten der Ebene angegeben sind, sehen wir, dass der Punkt relativ zur Achse symmetrisch zum gegebenen Punkt ist Oy hat die gleiche Ordinate wie der gegebene Punkt und eine Abszisse, deren Absolutwert der Abszisse des gegebenen Punktes entspricht und deren Vorzeichen entgegengesetzt ist. Wir erhalten also die folgenden Koordinaten von Punkten, die relativ zur Achse symmetrisch zu diesen Punkten sind Oy :

A"(1; 2) ;

B"(-3; -1) ;

C"(2; -2) .

Beispiel 7. Im kartesischen Koordinatensystem werden Punkte auf der Ebene angegeben

A(3; 3) ;

B(2; -4) ;

C(-2; 1) .

Finden Sie die Koordinaten von Punkten, die relativ zum Ursprung symmetrisch zu diesen Punkten sind.

Lösung. Wir drehen das gerichtete Segment vom Ursprung zum gegebenen Punkt um 180 Grad um den Ursprung. In der Abbildung, in der die Quadranten der Ebene angegeben sind, sehen wir, dass ein Punkt, der relativ zum Koordinatenursprung symmetrisch zu diesem Punkt ist, eine Abszisse und eine Ordinate hat, die im absoluten Wert der Abszisse und der Ordinate des gegebenen Punktes entsprechen, aber entgegengesetztes Vorzeichen. Wir erhalten also die folgenden Koordinaten von Punkten, die relativ zum Ursprung symmetrisch zu diesen Punkten sind:

A"(-3; -3) ;

B"(-2; 4) ;

C(2; -1) .

Beispiel 8.

A(4; 3; 5) ;

B(-3; 2; 1) ;

C(2; -3; 0) .

Finden Sie die Koordinaten der Projektionen dieser Punkte:

1) im Flugzeug Oxy ;

2) im Flugzeug Oxz ;

3) zum Flugzeug Oyz ;

4) auf der Abszissenachse;

5) auf der Ordinatenachse;

6) auf der Anwendungsachse.

1) Projektion eines Punktes auf eine Ebene Oxy befindet sich auf dieser Ebene selbst und hat daher eine Abszisse und eine Ordinate, die der Abszisse und Ordinate eines bestimmten Punktes entsprechen, und eine Anwendung, die gleich Null ist. Wir erhalten also die folgenden Koordinaten der Projektionen dieser Punkte auf Oxy :

Axy (4; 3; 0);

Bxy (-3; 2; 0);

Cxy(2;-3;0).

2) Projektion eines Punktes auf eine Ebene Oxz befindet sich auf dieser Ebene selbst und hat daher eine Abszisse und ein Applikat gleich der Abszisse und ein Applikat eines bestimmten Punktes und eine Ordinate gleich Null. Wir erhalten also die folgenden Koordinaten der Projektionen dieser Punkte auf Oxz :

Axz (4; 0; 5);

Bxz (-3; 0; 1);

Cxz (2; 0; 0).

3) Projektion eines Punktes auf eine Ebene Oyz befindet sich auf dieser Ebene selbst und hat daher eine Ordinate und ein Applikat gleich der Ordinate und ein Applikat eines bestimmten Punktes und eine Abszisse gleich Null. Wir erhalten also die folgenden Koordinaten der Projektionen dieser Punkte auf Oyz :

Ayz(0; 3; 5);

Byz (0; 2; 1);

Cyz (0; -3; 0).

4) Wie aus dem theoretischen Teil dieser Lektion hervorgeht, liegt die Projektion eines Punktes auf die Abszissenachse auf der Abszissenachse selbst, also der Achse Ochse und hat daher eine Abszisse, die der Abszisse des Punktes selbst entspricht, und die Ordinate und das Applikat der Projektion sind gleich Null (da die Ordinate und die Applikatachse die Abszisse am Punkt 0 schneiden). Wir erhalten die folgenden Koordinaten der Projektionen dieser Punkte auf die Abszissenachse:

Ax(4;0;0);

Bx (-3; 0; 0);

Cx(2;0;0).

5) Die Projektion eines Punktes auf die Ordinatenachse befindet sich auf der Ordinatenachse selbst, also der Achse Oy und hat daher eine Ordinate, die der Ordinate des Punktes selbst entspricht, und die Abszisse und das Applikat der Projektion sind gleich Null (da die Abszissen- und Applikatachse die Ordinatenachse am Punkt 0 schneiden). Wir erhalten die folgenden Koordinaten der Projektionen dieser Punkte auf die Ordinatenachse:

Ay(0; 3; 0);

By (0; 2; 0);

Cy(0;-3;0).

6) Die Projektion eines Punktes auf die Applikatachse befindet sich auf der Applikatachse selbst, also der Achse Oz und hat daher ein Applikat, das dem Applikat des Punktes selbst entspricht, und die Abszisse und die Ordinate der Projektion sind gleich Null (da die Abszissen- und Ordinatenachse die Applikatenachse am Punkt 0 schneiden). Wir erhalten die folgenden Koordinaten der Projektionen dieser Punkte auf die Anwendungsachse:

Az (0; 0; 5);

Bz (0; 0; 1);

Cz(0; 0; 0).

Beispiel 9. Im kartesischen Koordinatensystem sind Punkte im Raum angegeben

A(2; 3; 1) ;

B(5; -3; 2) ;

C(-3; 2; -1) .

Finden Sie die Koordinaten der zu diesen Punkten symmetrischen Punkte in Bezug auf:

1) Flugzeug Oxy ;

2) Flugzeuge Oxz ;

3) Flugzeuge Oyz ;

4) Abszissenachsen;

5) Ordinatenachsen;

6) Achsen anwenden;

7) Koordinatenursprung.

1) „Verschieben“ Sie den Punkt auf der anderen Seite der Achse Oxy Oxy, hat eine Abszisse und Ordinate, die der Abszisse und Ordinate eines bestimmten Punktes entsprechen, und ein Applikat, dessen Größe dem Aplikat eines bestimmten Punktes entspricht, dessen Vorzeichen jedoch entgegengesetzt ist. Wir erhalten also die folgenden Koordinaten von Punkten, die symmetrisch zu den Daten relativ zur Ebene sind Oxy :

A"(2; 3; -1) ;

B"(5; -3; -2) ;

C"(-3; 2; 1) .

2) „Verschieben“ Sie den Punkt auf der anderen Seite der Achse Oxz auf die gleiche Entfernung. Aus der Abbildung, die den Koordinatenraum darstellt, sehen wir, dass ein Punkt symmetrisch zu einem bestimmten Punkt relativ zur Achse ist Oxz, hat eine Abszisse und ein Applikat, die der Abszisse und dem Applikat eines bestimmten Punktes entsprechen, und eine Ordinate, deren Größe der Ordinate eines bestimmten Punktes entspricht, jedoch ein entgegengesetztes Vorzeichen hat. Wir erhalten also die folgenden Koordinaten von Punkten, die symmetrisch zu den Daten relativ zur Ebene sind Oxz :

A"(2; -3; 1) ;

B"(5; 3; 2) ;

C"(-3; -2; -1) .

3) „Verschieben“ Sie den Punkt auf der anderen Seite der Achse Oyz auf die gleiche Entfernung. Aus der Abbildung, die den Koordinatenraum darstellt, sehen wir, dass ein Punkt symmetrisch zu einem bestimmten Punkt relativ zur Achse ist Oyz hat eine Ordinate und ein Aplikat, die der Ordinate und einem Aplikat eines gegebenen Punktes entsprechen, und eine Abszisse, deren Wert der Abszisse eines gegebenen Punktes entspricht, das Vorzeichen jedoch entgegengesetzt ist. Wir erhalten also die folgenden Koordinaten von Punkten, die symmetrisch zu den Daten relativ zur Ebene sind Oyz :

A"(-2; 3; 1) ;

B"(-5; -3; 2) ;

C"(3; 2; -1) .

In Analogie zu symmetrischen Punkten auf einer Ebene und Punkten im Raum, die symmetrisch zu Daten relativ zu Ebenen sind, stellen wir fest, dass im Fall der Symmetrie in Bezug auf eine Achse des kartesischen Koordinatensystems im Raum die Koordinate auf der Achse in Bezug auf Der Punkt, an dem die Symmetrie gegeben ist, behält sein Vorzeichen, und die Koordinaten auf den anderen beiden Achsen haben in ihrem Absolutwert den gleichen Wert wie die Koordinaten eines gegebenen Punktes, haben aber ein entgegengesetztes Vorzeichen.

4) Die Abszisse behält ihr Vorzeichen, aber die Ordinate und die Applikate ändern ihr Vorzeichen. Wir erhalten also die folgenden Koordinaten von Punkten, die relativ zur Abszissenachse symmetrisch zu den Daten sind:

A"(2; -3; -1) ;

B"(5; 3; -2) ;

C"(-3; -2; 1) .

5) Die Ordinate behält ihr Vorzeichen, aber die Abszisse und das Applikat ändern das Vorzeichen. Wir erhalten also die folgenden Koordinaten von Punkten, die symmetrisch zu den Daten relativ zur Ordinatenachse sind:

A"(-2; 3; -1) ;

B"(-5; -3; -2) ;

C"(3; 2; 1) .

6) Das Applikat behält sein Vorzeichen, aber Abszisse und Ordinate ändern das Vorzeichen. Wir erhalten also die folgenden Koordinaten von Punkten, die symmetrisch zu den Daten relativ zur Anwendungsachse sind:

A"(-2; -3; 1) ;

B"(-5; 3; 2) ;

C"(3; -2; -1) .

7) In Analogie zur Symmetrie im Fall von Punkten auf einer Ebene sind im Fall der Symmetrie um den Koordinatenursprung alle Koordinaten eines zu einem bestimmten Punkt symmetrischen Punktes im Absolutwert gleich den Koordinaten eines bestimmten Punktes. aber ihnen im Vorzeichen entgegengesetzt. Wir erhalten also die folgenden Koordinaten von Punkten, die symmetrisch zu den Daten relativ zum Ursprung sind.

Gleichung eines Kreises auf der Koordinatenebene

Definition 1. Zahlenachse ( Zahlenstrahl, Koordinatenstrahl) Ox ist die Gerade, auf der Punkt O ausgewählt wird Ursprung (Koordinatenursprung)(Abb.1), Richtung

Ö → X

aufgeführt als positive Richtung und es wird ein Segment markiert, dessen Länge angenommen wird Längeneinheit.

Definition 2. Ein Segment, dessen Länge als Längeneinheit angenommen wird, wird Maßstab genannt.

Jeder Punkt auf der Zahlenachse hat eine Koordinate, die eine reelle Zahl ist. Die Koordinate des Punktes O ist Null. Die Koordinate eines beliebigen Punktes A, der auf dem Strahl Ox liegt, ist gleich der Länge des Segments OA. Die Koordinate eines beliebigen Punktes A der numerischen Achse, der nicht auf dem Strahl Ox liegt, ist negativ und entspricht im Absolutwert der Länge des Segments OA.

Definition 3. Rechteckiges kartesisches Koordinatensystem Oxy in der Ebene Rufen Sie zwei gegenseitig an aufrecht numerische Achsen Ox und Oy mit den gleichen Maßstab Und gemeinsamer Bezugspunkt am Punkt O und so, dass die Drehung vom Strahl Ox im Winkel von 90° zum Strahl Oy in der Richtung erfolgt gegen den Uhrzeigersinn(Abb. 2).

Notiz. Das in Abbildung 2 dargestellte rechtwinklige kartesische Koordinatensystem Oxy wird aufgerufen rechtes Koordinatensystem, im Gegensatz zu linke Koordinatensysteme, bei dem die Drehung des Strahls Ox im Winkel von 90° zum Strahl Oy im Uhrzeigersinn erfolgt. In diesem Leitfaden haben wir Wir betrachten nur rechtshändige Koordinatensysteme, ohne es konkret zu spezifizieren.

Wenn wir in der Ebene ein System rechtwinkliger kartesischer Koordinaten Oxy einführen, erhält jeder Punkt der Ebene einen Wert zwei Koordinaten – Abszisse Und Ordinate, die wie folgt berechnet werden. Sei A ein beliebiger Punkt auf der Ebene. Lassen Sie uns Senkrechte von Punkt A fallen lassen A.A. 1 und A.A. 2 zu den Geraden Ox bzw. Oy (Abb. 3).

Definition 4. Die Abszisse von Punkt A ist die Koordinate des Punktes A 1 auf der Zahlenachse Ox, die Ordinate von Punkt A ist die Koordinate des Punktes A 2 auf der Zahlenachse Oy.

Bezeichnung Koordinaten (Abszisse und Ordinate) des Punktes Im rechtwinkligen kartesischen Koordinatensystem wird üblicherweise A mit Oxy (Abb. 4) bezeichnet A(X;j) oder A = (X; j).

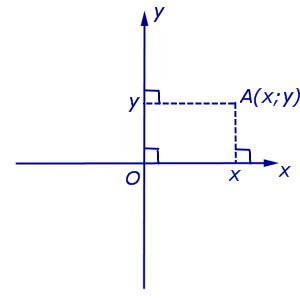
Notiz. Punkt O, genannt Herkunft, hat Koordinaten Ö(0 ; 0) .

Definition 5. Im rechteckigen kartesischen Koordinatensystem Oxy wird die numerische Achse Ox als Abszissenachse und die numerische Achse Oy als Ordinatenachse bezeichnet (Abb. 5).

Definition 6. Jedes rechteckige kartesische Koordinatensystem unterteilt die Ebene in 4 Viertel (Quadranten), deren Nummerierung in Abbildung 5 dargestellt ist.

Definition 7. Die Ebene, auf der ein rechtwinkliges kartesisches Koordinatensystem gegeben ist, heißt Koordinatenebene.

Notiz. Die Abszissenachse wird auf der Koordinatenebene durch die Gleichung angegeben j= 0, die Ordinatenachse ist auf der Koordinatenebene durch die Gleichung gegeben X = 0.

Aussage 1. Abstand zwischen zwei Punkten Koordinatenebene

A 1 (X 1 ;j 1) Und A 2 (X 2 ;j 2)

berechnet nach der Formel

Nachweisen . Betrachten Sie Abbildung 6.