Главная » Дизайн дома » Как освободиться от иррациональности. Как в дроби избавиться от иррациональности в знаменателе. Последовательное применение различных способов преобразования

Как освободиться от иррациональности. Как в дроби избавиться от иррациональности в знаменателе. Последовательное применение различных способов преобразования

Урок №1 Тема урока: «Освобождение от иррациональности в знаменателе дроби»

Цели:

Образовательная:

Развивающая:

Воспитательная: воспитание последовательности в своих действиях.

Тип урока: изучение нового

Стандарт урока:

уметь находить способ избавления от иррациональности

понимать смысл «сопряженное выражение»

уметь избавляться от иррациональности в знаменателе.

Оборудование: карточки к самостоятельной работе.

Ход урока

Немного юмора:

Извлекать корни умеешь? – спрашивает учитель

Да, конечно. Нужно потянуть за стебель растения посильнее, и корень его извлечётся из почвы.

Нет, я имел в виду другой корень, например, из девяти.

Это будет «девя», так как «ть»-суффикс.

Я имею в виду корень квадратный.

Квадратных корней не бывает. Они бывают мочковатые и стержневые.

Арифметический квадратный корень из девяти.

Так бы и сказали! Квадратный корень из девяти =3!

А вы корни извлекать умеете?

2. «Повторение – мать учения».

(8 мин)

2.Проверка дом/з № 168 1)4; 2)10; 3)4;4) 8

3.Разминка. Выполни действия (Слайд 1). Проверка по кругу против часовой стрелки.

1. Подбери неизвестный множитель (Слайд2)

Деление на группы: по выбранным фигурам.

Проверяют в парах сменного состава.

Работают индивидуально и проверяют, оценивая в баллах.

(Приложение 1)

3. «Книга – книгой, а мозгами двигай» (5 мин)

(Слайд 3) Два друга решали уравнение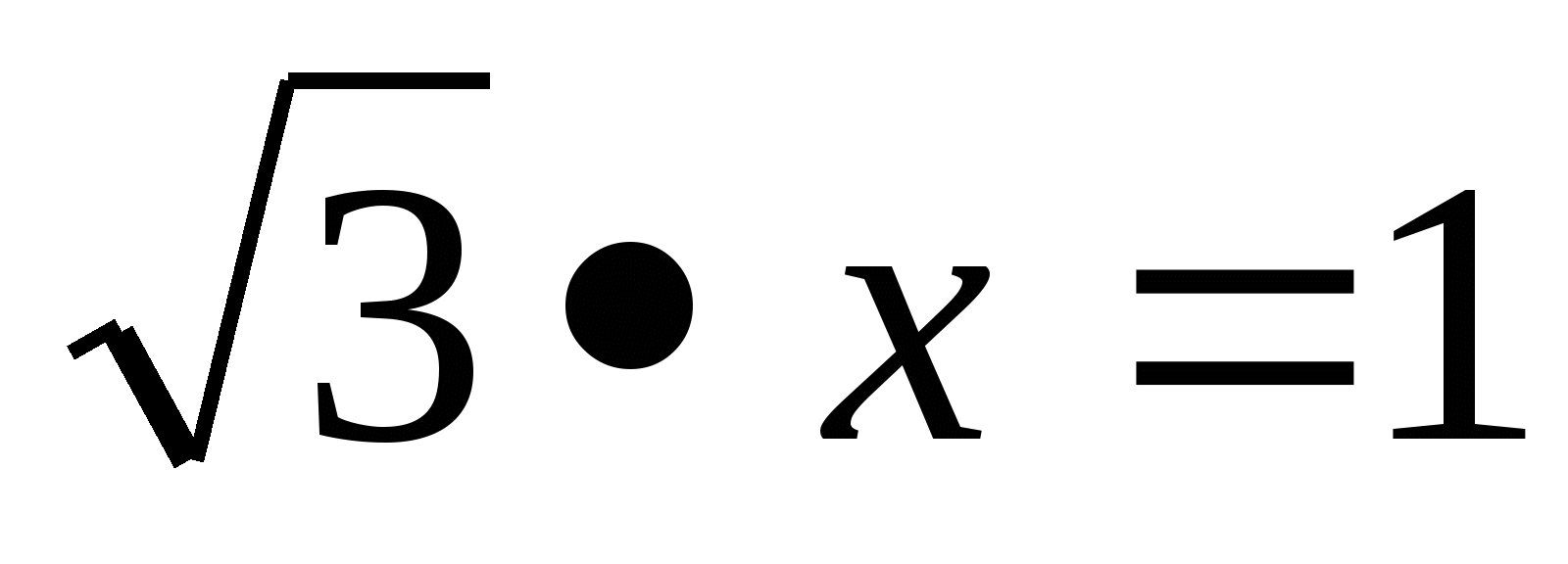
и получили разные ответы. Один из них подобрал х = , сделал проверку. Второй находил неизвестный множитель делением произведения на
и получил х = 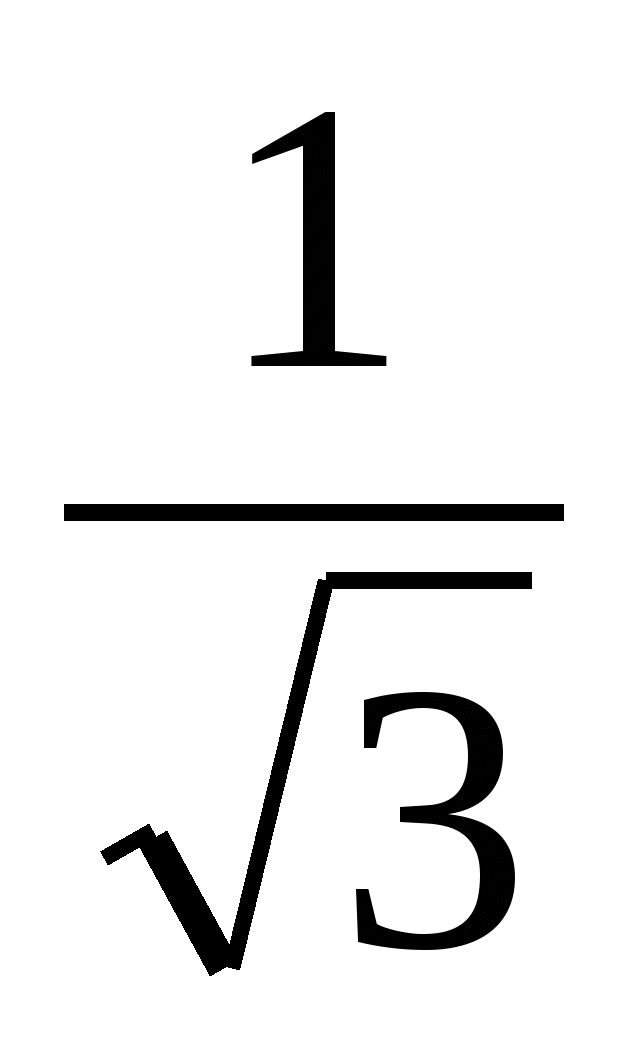. Кто из них прав? Может ли линейное уравнение иметь два корня? Самым удобным для вычислений является выражение, не содержащее иррациональности в знаменателе.

Тема урока (Слайд 4): Освобождение от иррациональности в знаменателе дроби

Цели (Слайд 5): ознакомиться со способами избавления от иррациональности в знаменатели дроби. Развитие умения освобождать знаменатель от иррациональности;

Решают и проверяют в парах сменного состава.

Обсуждают ситуацию и приходят к выводу.

Записывают тему

Формулируют цели : ознакомиться со способами избавления от иррациональности в знаменатели дроби.

развитие умения определять способ освобождения от иррациональности;

4. Работа над новым материалом.

(10 мин)

Как избавиться от иррациональности в знаменателе? Хотите узнать?

Работа в группах над новым материалом

Выступление групп

Закрепление (Слайд 6)

Работают с опорным конспектом. (Приложение 2)

Решают примеры.

(Приложение 3)

Обмениваются информацией.

5. Зарядка (3 мин)

Делают зарядку

6. Самостоятельная работа

(10 мин)

По разноуровневым карточкам

1-в:

2-в:

3-в:

Выполняют индивидуально, проверяют меняясь тетрадями с другой группой.

Баллы заносят в оценочную карту группы.

(Приложение 1)

7.Творческое задание

(2 мин)

Мартышка – апельсинов продавщица,(Слайд 7)

Приехав как – то раз к себе на дачу,

Нашла там с радикалами задачу.

Разбрасывать их стала все подряд.

Мы просим вас, девчонки и мальчишки,

Решить задачу на хвосте мартышки.

Как вы думаете мы закончили изучать эту тему? Продолжим на следующем уроке.

Рассуждают о том, что это им предстоит узнать на следующем уроке.

8. Задание на дом: (2 мин)

П.19(Слайд 7)

1 уровень: №170 (1-6)

2 уровень: №170 (1-6 и 9,12)

Творческое задание: Мартышкина задача.

Записывают

9.Итог урока. Рефлексия

(3 мин)

Две звезды и пожелание на стикерах прикрепляются на выбранный смайлик (Слайд 7)

Баллы переводят в оценку и сдают учителю оценочную карту группы.

ПРИЛОЖЕНИЕ 1

Оценочная карта группы.

0-8 баллов

Подбери множитель

0-8 баллов

Работа в группе над новым материалом

0-5 баллов

Сам. работа

0-5 баллов

Активность на уроке

0-5 баллов

ПРИЛОЖЕНИЕ 2

Опорный конспект

Если знаменатель алгебраической дроби содержит знак квадратного корня, то говорят, что в знаменателе содержится иррациональность. Преобразование выражения к такому виду, чтобы в знаменателе дроби не оказалось знаков квадратных корней, называют освобождением от иррациональности в знаменателе

Рассмотрим задачу из алгебры многочленов.

Задача 4.1

Пусть а является корнем многочлена х 3 + 6х - 3. Нужно освободиться от алгебраической иррациональности в знаменателе дроби

Т.е. представить дробь в виде многочлена от а с рацио-

нальными коэффициентами.

Решение. Знаменатель дроби есть значение от а многочлена fix) =х 2 + 5, а минимальным многочленом алгебраического элемента а является ф(х) =х 3 + 6х- 3, поскольку этот многочлен неприводим над полем Q (по критерию Эйзенштейна при простом р = 3). Найдем НОДОс 3 + 6х - 3, х 2 + 5) с помощью алгоритма Евклида:

Обобщим ситуацию и рассмотрим общую задачу.

Задача об освобождении от алгебраической иррациональности в знаменателе дроби

Пусть а - алгебраическая иррациональность над полем Р с ми-

, . „ а к а к +a k _,a k ~ l -f-. + aia + Oo

нимальным многочленом фОО и В = - - 1

Ъ т а т + bro-ioc" 1 - 1 +... + bja + b 0

где коэффициенты многочленов в числителе и знаменателе дроби принадлежат полю Р. Освободиться от алгебраической иррациональности в знаменателе дроби, т.е. представить (3 в виде

где коэффициенты принадлежат полю Р.

Решение. Обозначим/)*) = b nl x" + b m _ 1 x nl_1 +... + b } x + b 0 и у =/(а). Поскольку у ^ 0, то по свойству минимального многочлена НОД(/(х), ф(х)) = 1. Используя алгоритм Евклида, находим многочлены u(x) и v(x), такие что f(x) и (х) + ф(х)у(х) = 1. Отсюда Да) и (а) + ф(а)у(а) = 1, а так как ф(а) = 0, тоДа)и(а) = 1. Следовательно, умножая числитель и знаменатель данной дроби на ц(а), в знаменателе получим единицу, и задача решена.

Заметим, что общий прием освобождения от алгебраической иррациональности в знаменателе дроби в случае комплексных а + Ы

чисел-приводит к известной процедуре умножения числи-

теля и знаменателя на число, сопряженное знаменателю.

Исторический экскурс

Впервые существование чисел, трансцендентных над полем Q, обнаружил Ж. Лиувилль (1809-1882) в работах 1844 и 1851 гг. Одним из трансцендентных чисел Лиувилля является число

Ш. Эрмит (1822-

а= У--. Вдесятичнойзаписиа = 0Д100010..

кл 10*

1901) доказал трансцендентность числа е в 1873 г., а К. Ф. Линде- ман (1852-1939) доказал в 1882 г. трансцендентность числа п. Эти результаты были получены очень не просто. В то же время совсем просто Г. Кантор (1845-1918) доказал, что трансцендентных чисел «значительно больше», чем алгебраических: трансцендентных чисел «столько же», сколько всех действительных чисел, в то время как алгебраических чисел «столько же», сколько всех натуральных чисел. Точнее, множество алгебраических чисел счетно, а множество трансцендентных чисел несчетно. Доказательство этого факта, устанавливая существование трансцендентных чисел, не дает рецепта получения ни одного из них. Такого рода теоремы существования чрезвычайно важны в математике уже тем, что вселяют веру в успех поиска объекта, существование которого доказано. Вместе с тем существует направление в математике, представители которого не признают чистых теорем существования, называя их неконструктивными. Наиболее яркими из этих представителей являются Л. Кронекер и Я. Брауэр.

В 1900 г. на Всемирном конгрессе математиков в Париже немецкий математик Д. Гильберт (1862-1943) сформулировал следующую проблему 22: Какова природа числа аР, где а и (3 - алгебраические числа, а ^ 0, а ^ 1 и степень алгебраического числа (3 не меньше 2? А. О. Гельфонд (1906-1968) доказал, что такие числа трансцендентны. Отсюда следует, в частности, что числа 2^, З г являются трансцендентными.

Данни Перич Кампана

Еще одна интересная книга для школьников, интересующихся , к сожалению, не переведенная на русский язык, — это книга “Математические приключения Даниэля” (Las Aventuras Matemáticas de Daniel) чилийского учителя математики Данни Перича Кампаны (Danny Perich Campana), человека весьма неординарного и интересного. Он не только учит ребятишек, но и пишет песни, выкладывает в Интеренет различные обучающие материалы по математике. Их можно найти на youtube, и на сайте http://www.sectormatematica.cl/ (разумеется, все материалы на испанском языке).

Здесь выкладываю одну главу из книги Данни Перича. Мне она показалась довольно интересной и полезной для школьников. Чтобы было понятно, о чем идет речь, скажу, что Даниэль и Камила работают в школе, они учителя.

Тайна избавления от иррациональности

— Камила, у меня сейчас возникает много проблем, когда пытаюсь объяснить, для чего применяется то, что проходим на уроке, — сказал Даниэль.

— Не очень понимаю, о чем ты говоришь.

— Я о том, что есть во всех школьных учебниках и даже книгах университетского уровня. Меня все равно не оставляют сомнения: зачем нужно избавляться от иррациональности в знаменателе? И я терпеть не могу рассказывать то, чего не понимаю уже столько времени, — жаловался Даниэль.

— Я тоже не знаю, откуда это идет и зачем это нужно, но должно быть какое-то логическое объяснение этому.

— Как-то я прочитал в одном научном журнале, что избавление от иррациональности в знаменателе позволяет получить результат с большей точностью, но никогда больше не встречал этого и не уверен, что это так и есть.

— А почему бы нам это не проверить? — спросила Камила.

— Ты права, — согласился Даниэль. — Вместо того, чтобы жаловаться, нужно попытаться самим сделать выводы. Тогда помоги мне…

— Конечно, теперь мне самой это интересно.

— Мы должны взять какие-нибудь выражения и избавиться от иррациональности в знаменателе, потом заменить корень на его значение и найти результат выражения до избавления от иррациональности в знаменателе и после и посмотреть, изменится ли что-нибудь.

— Разумеется, — согласилась Камила. — Давай так и сделаем.

— Возьмем, например, выражение , — сказал Даниэль и взял лист бумаги, чтобы записывать происходящее. — Умножим числитель и знаменатель на и получим .

— Будет правильно и может помочь нам сделать выводы, если мы рассмотрим другие иррациональные выражения, равные данному, — предложила Камила.

— Согласен, — сказал Даниэль, — я поделю числитель и знаменатель на , а ты домножь их на .

— У меня получилось . А у тебя?

— У меня , — ответил Даниэль. — Теперь вычислим исходное выражение и полученные, заменяя на его значение со всеми десятичными знаками, которые дает калькулятор. Получим:

— Не вижу ничего особенного, — сказала Камила. — Я ожидала какого-либо различия, которое оправдало бы избавление от иррациональности.

— Как я тебе уже говорил, я когда-то читал об этом в связи с приближением. Что ты скажешь, если мы заменим на менее точное число, например, на ?

— Пробуем и смотрим, что получилось.

Освобождение от иррациональности в знаменателе дроби

2015-06-13

Сопряженное иррациональное выражение

При преобразовании дробного алгебраического выражения, в знаменателе которого записано иррациональное выражение, обычно стремятся представить дробь так, чтобы ее знаменатель был рациональным. Если $A, B, C, D, \cdots$ - некоторые алгебраические выражения, то можно указать правила, с помощью которых можно освободиться от знаков радикала в знаменателе выражений вида

$\frac{A}{\sqrt[n]{B}}, \frac{A}{B+C \sqrt{D}}, \frac{A}{\sqrt{B} + c \sqrt{D}}, \frac{A}{ \sqrt{B} \pm \sqrt{C}}$ и т.д.

Во всех этих случаях освобождение от иррациональности производится умножением числителя и знаменателя дроби на множитель, выбранный так, чтобы его произведение на знаменатель дроби было рациональным.

1) Для освобождения от иррациональности в знаменателе дроби вида $A/ \sqrt[n]{B}$ умножаем числитель и знаменатель на $\sqrt[n]{B^{n-1}}$.
$\frac{A}{\sqrt[n]{B}} = \frac{A \sqrt[n]{B^{n-1}}}{\sqrt[n]{B} \sqrt[n]{B^{n-1}}} = \frac{A \sqrt[n]{B^{n-1}}}{B}$.

Пример 1. $\frac{4a^{2}b}{\sqrt{2ac}} = \frac{4a^{2}b \sqrt{4a^{2}c^{2}}}{2ac} = \frac{2ab}{c} \sqrt{4a^{2}c^{2}}$.

В случае дробей вида $\frac{A}{B+ C \sqrt{D}}, \frac{A}{\sqrt{B} + c \sqrt{D}}$ умножаем числитель и знаменатель на иррациональный множитель
$B – C \sqrt{D}$ или $\sqrt{B} – c \sqrt{D}$
соответственно, т. е. на сопряженное иррациональное выражение.

Смысл последнего действия состоит в том, что в знаменателе произведение суммы на разность преобразуется в разность квадратов, которая уже будет рациональным выражением.

Пример 2. Освободиться от иррациональности в знаменателе выражения:
а) $\frac{xy}{\sqrt{x^{2} + y^{2}} + x}$; б) $\frac{2}{\sqrt{5} - \sqrt{3}}$.

Решение, а) Умножаем числитель и знаменатель дроби на
выражение $\sqrt{x^{2} + y^{2}} - x$. Получаем (при условии, что $y \neq 0$)
$\frac{xy}{\sqrt{x^{2} + y^{2}} + x} = \frac{xy (\sqrt{x^{2} + y^{2}} - x)}{(x^{2} + y^{2}) – x^{2}} = \frac{x}{y} (\sqrt{x^{2} + y^{2}} - x)$;
б) $\frac{2}{\sqrt{5} - \sqrt{3}} = \frac{2(\sqrt{5} + \sqrt{3})}{5 - 3} = \sqrt{5} + \sqrt{3}$.
3) В случае выражений типа
$\frac{A}{B \pm C \sqrt{D}}, \frac{A}{\sqrt{B} \pm C \sqrt{D}}$
знаменатель рассматривается как сумма (разность) и умножается на неполный квадрат разности (суммы), чтобы получить сумму (разность) кубов. На тот же множитель умножается и числитель.

Пример 3. Освободиться от иррациональности в знаменателе выражений:
а)$\frac{3}{\sqrt{5} + 1}$; б)$\frac{1}{\sqrt{a} – 2 \sqrt{b}}$

Решение, а) Рассматривая знаменатель данной дроби как сумму чисел $\sqrt{5}$ и $1$, умножим числитель и знаменатель на неполный квадрат разности этих чисел:
$\frac{3}{\sqrt{5} + 1} = \frac{3 (\sqrt{5^{2}} - \sqrt{5} +1)}{(\sqrt{5} + 1)(\sqrt{5^{2}} - \sqrt{5} + 1)} = \frac{3(\sqrt{25} - \sqrt{5} + 1)}{(\sqrt{5})^{3} +1}$,
или окончательно:
$\frac{3}{\sqrt{5} + 1} = \frac{3(\sqrt{25} - \sqrt{5} + 1)}{6} = \frac{\sqrt{25} - \sqrt{5} + 1}{2}$
б) $\frac{1}{\sqrt{a} – 2 \sqrt{b}} = \frac{\sqrt{a^{2}} + 2 \sqrt{ab} + 4 \sqrt{b^{2}}}{(\sqrt{a})^{3} – (2 \sqrt{b})^{3}} = \frac{ \sqrt{a^{2}} + 2 \sqrt{ab} + 4 \sqrt{b^{2}}}{a-8b}$.

В некоторых случаях требуется выполнить преобразование противоположного характера: освободить дробь от иррациональности в числителе. Оно проводится совершенно аналогично.

Пример 4. Освободиться от иррациональности в числителе $\frac{\sqrt{a+b} - \sqrt{a-b}}{2b}$.
Решение. $ \frac{\sqrt{a+b} - \sqrt{a-b}}{2b} = \frac{(a+b) – (a-b)}{2b(\sqrt{a+b} + \sqrt{a-b})} = \frac{1}{\sqrt{a+b} + \sqrt{a-b}}$

При преобразовании дробного алгебраического выражения, в знаменателе которого записано иррациональное выражение, обычно стремятся представить дробь так, чтобы ее знаменатель был рациональным. Если A,B,C,D,... - некоторые алгебраические выражения, то можно указать правила, с помощью которых можно освободиться от знаков радикала в знаменателе выражений вида

1) Для освобождения от иррациональности в знаменателе дроби вида . В умножаем числитель и знаменатель на

Пример 1. .

2) В случае дробей вида . Умножаем числитель и знаменатель на иррациональный множитель

соответственно, т. е. на сопряженное иррациональное выражение.

Пример 2. Освободиться от иррациональности в знаменателе выражения:

Решение, а) Умножаем числитель и знаменатель дроби на выражение . Получаем (при условии, что )

3) В случае выражений типа

знаменатель рассматривается как сумма (разность) и умножается на неполный квадрат разности (суммы), чтобы получить сумму (разность) кубов ((20.11), (20.12)). На тот же множитель умножается и числитель.

Пример 3. Освободиться от иррациональности в знаменателе выражений: