Практическое занятие:" Построение сечений параллелепипеда". Построение сечений и разрезов на чертежах

Как известно, любой экзамен по математике содержит в качестве основной части решение задач. Умение решать задачи – основной показатель уровня математического развития.

Достаточно часто на школьных экзаменах, а так же на экзаменах, проводимых в ВУЗах и техникумах, встречаются случаи, когда ученики, показывающие хорошие результаты в области теории, знающие все необходимые определения и теоремы, запутываются при решении весьма простых задач.

За годы обучения в школе каждый ученик решает большое число задач, но при этом для всех учеников задачи предлагаются одни и те же. И если некоторые ученики усваивают общие правила и методы решения задач, то другие, встретившись с задачей незнакомого вида, даже не знают, как к ней подступиться.

Одной из причин такого положения является то, что если одни ученики вникают в ход решения задачи и стараются осознать и понять общие приёмы и методы их решения, то другие не задумываются над этим, стараются как можно быстрее решить предложенные задачи.

Многие учащиеся не анализируют решаемые задачи, не выделяют для себя общие приёмы и способы решения. В таких случаях задачи решаются только ради получения нужного ответа.

Так, например, многие учащиеся даже не знают, в чём суть решения задач на построение. А ведь задачи на построение являются обязательными задачами в курсе стереометрии. Эти задачи не только красивы и оригинальны в методах своего решения, но и имеют большую практическую ценность.

Благодаря задачам на построение развивается способность мысленно представлять себе ту или иную геометрическую фигуру, развивается пространственное мышление, логическое мышление, а так же геометрическая интуиция. Задачи на построение развивают навыки решения проблем практического характера.

Задачи на построения не являются простыми, так как единого правила или алгоритма для их решения не существует. Каждая новая задача уникальна и требует индивидуального подхода к решению.

Процесс решения любой задачи на построение – это последовательность некоторых промежуточных построений, приводящих к цели.

Построение сечений многогранников базируется на следующих аксиомах:

1) Если две точки прямой лежат в некоторой плоскости, то и вся прямая лежит в данной плоскости;

2) Если две плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.

Теорема: если две параллельные плоскости пересечены третьей плоскостью, то прямые пересечения параллельны.

Построить сечение многогранника плоскостью, проходящей через точки А, В и С. Рассмотрим следующие примеры.

Метод следов

I. Построить сечение призмы плоскостью, проходящей через данную прямую g (след) на плоскости одного из оснований призмы и точку А.

Случай 1.

Точка А принадлежит другому основанию призмы (или грани, параллельной прямой g) – секущая плоскость пересекает это основание (грань) по отрезку ВС, параллельному следу g.

Случай 2.

Точка А принадлежит боковой грани призмы:

Отрезок ВС прямой AD и есть пересечение данной грани с секущей плоскостью.

Случай 3.

Построение сечения четырехугольной призмы плоскостью, проходящей через прямую g в плоскости нижнего основания призмы и точку А на одном из боковых ребер.

II. Построить сечение пирамиды плоскостью, проходящей через данную прямую g (след) на плоскости основания пирамиды и точку А.

Для построения сечения пирамиды плоскостью достаточно построить пересечения ее боковых граней с секущей плоскостью.

Случай 1.

Если точка А принадлежит грани, параллельной прямой g, то секущая плоскость пересекает эту грань по отрезку ВС, параллельному следу g.

Случай 2.

Если точка А, принадлежащая сечению, расположена на грани, не параллельной грани следу g, то:

1) строится точка D, в которой плоскость грани пересекает данный след g;

2) проводится прямая через точки А и D.

Отрезок ВС прямой АD и есть пересечение данной грани с секущей плоскостью.

Концы отрезка ВС принадлежат и соседним граням. Поэтому описанным способом можно построить пересечение этих граней с секущей плоскостью. И т. д.

Случай 3.

Построение сечения четырехугольной пирамиды плоскостью, проходящей через сторону основания и точку А на одном из боковых ребер.

Задачи на построение сечений через точку на грани

1. Построить сечение тетраэдра АВСD плоскостью, проходящей через вершину С и точки М и N на гранях АСD и АВС соответственно.

Точки С и М лежат на грани АСD, значит, и прямая СМ лежит в плоскости этой грани (рис. 1).

Пусть Р – точка пересечения прямых СМ и АD. Аналогично, точки С и N лежат в грани АСВ, значит прямая СN лежит в плоскости этой грани. Пусть Q – точка пересечения прямых СN и АВ. Точки Р и Q принадлежат и плоскости сечения, и грани АВD. Поэтому отрезок РQ – сторона сечения. Итак, треугольник СРQ – искомое сечение.

2. Построить сечение тетраэдра АВСD плоскостью MPN, где точки M, N, P лежат соответственно на ребре АD, в грани ВСD и в грани АВС, причем MN не параллельно плоскости грани АВС (рис. 2) .

Остались вопросы? Не знаете, как построить сечение многогранника?
Чтобы получить помощь репетитора – .
Первый урок – бесплатно!

blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Практическое занятие: «Параллелепипед. Построение сечений параллелепипеда ».

1. Цель практической работы : . Закрепить знания теоретического материала о многогранниках, навыки решения задач на построение сечений, умения анализировать чертеж.

2.Дидактическое оснащение практической работы : АРМ, модели и развёртки многогранников, измерительные инструменты, ножницы, клей, плотная бумага.

Время:2 часа

Задания к работе:

Задание 1

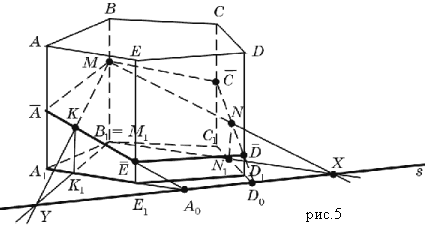
Построить сечение параллелепипеда ABCDA 1 B 1 C 1 D 1 плоскостью, проходящей через точки M, N, P, лежащие, на прямых, соответственно, A 1 B 1, А D , DC

Образец и последовательность решения задачи:

1.Точки N и P лежат в плоскости сечения и в плоскости нижнего основания параллелепипеда. Построим прямую, проходящую через эти точки. Эта прямая является следом секущей плоскости на плоскость основания параллелепипеда.

2.Продолжим прямую, на которой лежит сторона AB параллелепипеда. Прямые AB и NP пересекутся в некоторой точке S. Эта точка принадлежит плоскости сечения.

3.Так как точка M также принадлежит плоскости сечения и пересекает прямую АА 1 в некоторой точке Х.

4.Точки X и N лежат в одной плоскости грани АА 1 D 1 D, соединим их и получим прямую XN.

5.Так как плоскости граней параллелепипеда параллельны, то через точку M можно провести прямую в грани A 1 B 1 C 1 D 1 , параллельную прямой NP. Эта прямая пересечет сторону В 1 С 1 в точке Y.

6.Аналогично проводим прямую YZ, параллельно прямой XN. Соединяем Z с P и получаем искомое сечение – MYZPNX.

Задание 2

Вариант1. Построить сечение параллелепипеда АВСDА1В1С1D1 плоскостью, заданной следующими точками M , N и P

1 Уровень: Все три точки лежит на рёбрах, выходящих из вершиныА

2 Уровень. M лежит в грани AA1D1D, N лежит в грани АА1В1В, P лежит в грани СС1D1D.

3 Уровень. M лежит на диагонали B1D, N лежит на диагонали АС1, P лежит на ребре С1D1.

Вариант2. Построить сечение параллелепипеда АВСDА1В1С1D1 плоскостью, проходящей через прямую DQ, где точка Q лежит на ребре СС1 и точку Р, заданную следующим образом

1 Уровень: Все три точки лежит на рёбрах, выходящих из вершиныС

2 Уровень: М лежит на продолжении ребра А1В1, причем точка А1 находится между точками В1 и Р.

3 Уровень: Р лежит на диагонали В1D

Порядок выполнения работы:

1.Изучите теоретический материал по темам:

Параллелепипед.

Прямой параллелепипед.

Наклонный параллелепипед.

Противолежащие грани параллелепипеда.

Свойства диагоналей параллелепипеда.

П онятие секущей плоскости и правила её построения.

Какие виды многоугольников получаются в сечении куба и параллелепипеда.

2. Постройте параллелепипед ABCDA 1 B 1 C 1 D 1

3.Разберите решение задачи № 1

4.Последовательно постройте сечение параллелепипеда ABCDA 1 B 1 C 1 D 1 плоскостью, проходящей через точки P, Q, R задачи № 1.

5.Постройте ещё три параллелепипеда и выделите на них сечения к задачам 1, 2, и 3 уровней

Критерии оценивания :

Литература: Атанасян Л.С. Геометрия: Учебник для 10-11 кл. общеобразоват. учреждений. Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кодомцев и др. - М.: Просвещение, 2010г Зив Б.Г. Задачи по геометрии: Пособие для учащихся 7-11 кл. общеобразоват. учреждений. / Б.Г. Зив, В.М. Мейлер, А.Г. Баханский. - М.: Просвещение, 2010. В. Н. ЛитвиненкоЗадачи на развитие пространственных представлений. Книга для учителя. - М.: Просвещение, 2010г

Дидактический материал к заданию практического занятия

К задаче № 1:

Некоторые возможные сечения:

Построить сечения параллелепипеда плоскостью, проходящей через данные точки

На этом уроке мы рассмотрим тетраэдр и его элементы (ребро тетраэдра, поверхность, грани, вершины). И решим несколько задач на построение сечений в тетраэдре, используя общий метод для построения сечений.

Тема: Параллельность прямых и плоскостей

Урок: Тетраэдр. Задачи на построение сечений в тетраэдре

Как построить тетраэдр? Возьмем произвольный треугольник АВС . Произвольную точку D , не лежащую в плоскости этого треугольника. Получим 4 треугольника. Поверхность, образованная этими 4 треугольниками, и называется тетраэдром (Рис. 1.). Внутренние точки, ограниченные этой поверхностью, также входят в состав тетраэдра.

Рис. 1. Тетраэдр АВСD

Элементы тетраэдра
А, B , C , D - вершины тетраэдра .
AB , AC , AD , BC , BD , CD - ребра тетраэдра .
ABC , ABD , BDC , ADC - грани тетраэдра .

Замечание: можно принять плоскость АВС за основание тетраэдра , и тогда точка D является вершиной тетраэдра . Каждое ребро тетраэдра является пересечением двух плоскостей. Например, ребро АВ - это пересечение плоскостей АВ D и АВС . Каждая вершина тетраэдра - это пересечение трех плоскостей. Вершина А лежит в плоскостях АВС , АВ D , А D С . Точка А - это пересечение трех означенных плоскостей. Этот факт записывается следующим образом: А = АВС ∩ АВ D ∩ АС D .

Тетраэдр определение

Итак, тетраэдр - это поверхность, образованная четырмя треугольниками.

Ребро тетраэдра - линия перечесения двух плоскостей тетраэдра.

Составьте из 6 спичек 4 равных треугольника. На плоскости решить задачу не получается. А в пространстве это сделать легко. Возьмем тетраэдр. 6 спичек - это его ребра, четыре грани тетраэдра и будут четырьмя равными треугольниками. Задача решена.

Дан тетраэдр АВС D . Точка M принадлежит ребру тетраэдра АВ , точка N принадлежит ребру тетраэдра В D и точка Р принадлежит ребру D С (Рис. 2.). Постройте сечение тетраэдра плоскостью MNP .

Рис. 2. Рисунок к задаче 2 - Построить сечение тетраэдра плоскостью

Решение :
Рассмотрим грань тетраэдра D ВС . В этой грани точки N и P принадлежат грани D ВС , а значит, и тетраэдру. Но по условию точки N, P принадлежат секущей плоскости. Значит, NP - это линия пересечения двух плоскостей: плоскости грани D ВС и секущей плоскости. Предположим, что прямые NP и ВС не параллельны. Они лежат в одной плоскости D ВС. Найдем точку пересечения прямых NP и ВС . Обозначим ее Е (Рис. 3.).

Рис. 3. Рисунок к задаче 2. Нахождение точки Е

Точка Е принадлежит плоскости сечения MNP , так как она лежит на прямой NР , а прямая NР целиком лежит в плоскости сечения MNP .

Также точка Е лежит в плоскости АВС , потому что она лежит на прямой ВС из плоскости АВС .

Получаем, что ЕМ - линия пересечения плоскостей АВС и MNP, так как точки Е и М лежат одновременно в двух плоскостях - АВС и MNP. Соединим точки М и Е , и продолжим прямую ЕМ до пересечения с прямой АС . Точку пересечения прямых ЕМ и АС обозначим Q .

Итак, в этом случае NPQМ - искомое сечение.

Рис. 4. Рисунок к задаче 2.Решение задачи 2

Рассмотрим теперь случай, когда NP параллельна BC . Если прямая NP параллельна какой-нибудь прямой, например, прямой ВС из плоскости АВС , то прямая NP параллельна всей плоскости АВС .

Искомая плоскость сечения проходит через прямую NP , параллельную плоскости АВС , и пересекает плоскость по прямой МQ . Значит, линия пересечения МQ параллельна прямой NP . Получаем, NPQМ - искомое сечение.

Точка М лежит на боковой грани А D В тетраэдра АВС D . Постройте сечение тетраэдра плоскостью, которое проходит через точку М параллельно основанию АВС .

Рис. 5. Рисунок к задаче 3 Построить сечение тетраэдра плоскостью

Решение:
Секущая плоскость φ параллельна плоскости АВС по условию, значит, эта плоскость φ параллельна прямым АВ , АС , ВС .
В плоскости АВ D через точку М проведем прямую PQ параллельно АВ (рис. 5). Прямая PQ лежит в плоскости АВ D . Аналогично в плоскости АС D через точку Р проведем прямую РR параллельно АС . Получили точку R . Две пересекающиеся прямые PQ и РR плоскости РQR соответственно параллельны двум пересекающимся прямым АВ и АС плоскости АВС , значит, плоскости АВС и РQR параллельны. РQR - искомое сечение. Задача решена.

Дан тетраэдр АВС D . Точка М - точка внутренняя, точка грани тетраэдра АВ D . N - внутренняя точка отрезка D С (Рис. 6.). Построить точку пересечения прямой NM и плоскости АВС .

Рис. 6. Рисунок к задаче 4

Решение:
Для решения построим вспомогательную плоскость D МN . Пусть прямая D М пересекает прямую АВ в точке К (Рис. 7.). Тогда, СК D - это сечение плоскости D МN и тетраэдра. В плоскости D МN лежит и прямая NM , и полученная прямая СК . Значит, если NM не параллельна СК , то они пересекутся в некоторой точке Р . Точка Р и будет искомая точка пересечения прямой NM и плоскости АВС .

Рис. 7. Рисунок к задаче 4. Решение задачи 4

Дан тетраэдр АВС D . М - внутренняя точка грани АВ D . Р - внутренняя точка грани АВС . N - внутренняя точка ребра D С (Рис. 8.). Построить сечение тетраэдра плоскостью, проходящей через точки М , N и Р .

Рис. 8. Рисунок к задаче 5 Построить сечение тетраэдра плоскостью

Решение:
Рассмотрим первый случай, когда прямая MN не параллельна плоскости АВС . В прошлой задаче мы нашли точку пересечения прямой MN и плоскости АВС . Это точка К , она получена с помощью вспомогательной плоскости D МN , т.е. мы проводим D М и получаем точку F . Проводим СF и на пересечении MN получаем точку К .

Рис. 9. Рисунок к задаче 5. Нахождение точки К

Проведем прямую КР . Прямая КР лежит и в плоскости сечения, и в плоскости АВС . Получаем точки Р 1 и Р 2 . Соединяем Р 1 и М и на продолжении получаем точку М 1 . Соединяем точку Р 2 и N . В результате получаем искомое сечение Р 1 Р 2 NМ 1 . Задача в первом случае решена.
Рассмотрим второй случай, когда прямая MN параллельна плоскости АВС . Плоскость МNР проходит через прямую МN параллельную плоскости АВС и пересекает плоскость АВС по некоторой прямой Р 1 Р 2 , тогда прямая Р 1 Р 2 параллельна данной прямой MN (Рис. 10.).

Рис. 10. Рисунок к задаче 5. Искомое сечение

Теперь проведем прямую Р 1 М и получим точку М 1 . Р 1 Р 2 NМ 1 - искомое сечение.

Итак, мы рассмотрели тетраэдр, решили некоторые типовые задачи на тетраэдр. На следующем уроке мы рассмотрим параллелепипед.

1. И. М. Смирнова, В. А. Смирнов. - 5-е издание, исправленное и дополненное - М. : Мнемозина, 2008. - 288 с. : ил. Геометрия. 10-11 класс: учебник для учащихся общеобразовательных учреждений (базовый и профильный уровни)

2. Шарыгин И. Ф. - М.: Дрофа, 1999. - 208 с.: ил. Геометрия. 10-11 класс: Учебник для общеобразовательных учебных заведений

3. Е. В. Потоскуев, Л. И. Звалич. - 6-е издание, стереотип. - М. : Дрофа, 008. - 233 с. :ил. Геометрия. 10 класс: Учебник для общеобразовательных учреждений с углубленным и профильным изучением математики

Дополнительные веб-ресурсы

2. Как построить сечение тетраэдра. Математика ().

3. Фестиваль педагогических идей ().

Сделай дома задачи по теме "Тетраэдр", как находить ребро тетраэдра, грани тетраэдра, вершины и поверхность тетраэдра

1. Геометрия. 10-11 класс: учебник для учащихся общеобразовательных учреждений (базовый и профильный уровни) И. М. Смирнова, В. А. Смирнов. - 5-е издание, исправленное и дополненное - М.: Мнемозина, 2008. - 288 с.: ил. Задания 18, 19, 20 стр. 50

2. Точка Е середина ребра МА тетраэдра МАВС . Постройте сечение тетраэдра плоскостью, проходящей через точки В, С и Е .

3. В тетраэдре МАВС точка М принадлежит грани АМВ, точка Р - грани ВМС, точка К - ребру АС. Постройте сечение тетраэдра плоскостью, проходящей через точки М, Р, К.

4. Какие фигуры могут получиться в результате пересечения плоскостью тетраэдра?

Аксиомы планиметрии:

В различных учебниках свойства прямых и плоскостей могут быть представлены по-разному, в виде аксиомы, следствия из нее, теоремы, леммы и т.д. Рассмотрим учебник Погорелова А.В.

Прямая разбивает плоскость на две полуплоскости.

0

От любой полупрямой в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180 0 , и только один.

Каков бы ни был треугольник, существует равный ему треугольник в заданном расположении относительно данной полупрямой.

Через точку, не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной.

Аксиомы стереометрии:

Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие этой плоскости, и точки не принадлежащие ей.

Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.

Если две различные прямые имеют общую точку, то через них можно провести плоскость, и притом только одну.

Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.

Через любые две точки можно провести прямую, и только одну.

Из трех точек на прямой одна и только одна лежит между двумя другими.

Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.

Прямая, принадлежащая плоскости, разбивает эту плоскость на две полуплоскости.

Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен 180 0 . Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.

На любой полупрямой от ее начальной точки можно отложить отрезок заданной длины, и только один.

От полупрямой на содержащей ее плоскости в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180 0 , и только один.

Каков бы ни был треугольник, существует равный ему треугольник в данной плоскости в заданном расположении относительно данной полупрямой в этой плоскости.

На плоскости через данную точку, не лежащую на данной прямой, можно провести не более одной прямой, параллельной данной.

Сечение

В пространстве две фигуры, для нашего случая плоскость и многогранник могут иметь следующее взаимное расположение: не пересекаются, пересекаются в точке, пересекаются по прямой и плоскость пересекает многогранник по его внутренности (рис.1), и при этом образуют следующие фигуры:

а) пустая фигура (не пересекаются)

б) точка

в) отрезок

г) многоугольник

Если в пересечении многогранника и плоскости есть многоугольник, то этот многоугольник называется сечением многогранника с плоскостью .

рис.1

Определение. Сечением пространственного тела (например, многогранника) называется фигура, получающаяся в пересечении тела с плоскостью.

Секущей плоскостью многогранника назовем любую плоскость, по обе стороны от которой имеются точки данного многогранника.

Будем рассматривать только случай, когда плоскость пересекает многогранник по его внутренности. При этом, пересечением данной плоскости с каждой гранью многогранника будет некоторый отрезок.

Если плоскости пересекаются по прямой, то прямую называют следом одной из этих плоскостей на другой.

В общем случае секущая плоскость многогранника пересекает плоскость каждой его грани (а также любую другую секущую плоскость этого многогранника). Она пересекает и каждую из прямых, на которых лежат ребра многогранника.

Прямую, по которой секущая плоскость пересекает плоскость какой-либо грани многогранника, называют следом секущей плоскости на плоскости этой грани, а точку, в которой секущая плоскость пересекает прямую, содержащую какое – либо ребро многогранника, называют следом секущей плоскости на этой прямой. Эта точка является и следом прямой на секущей плоскости. Если секущая плоскость пересекает непосредственно грань многогранника, то можно говорить о следе секущей плоскости на грани, и, аналогично, о следе секущей плоскости на ребре многогранника, то есть о следе ребра на секущей плоскости.

Так как прямая однозначно определяется двумя точками, то для нахождения следа секущей плоскости на любой другой плоскости и, в частности, на плоскости любой грани многогранника, достаточно построить две общие точки плоскостей

Для построения следа секущей плоскости, а также для построения сечения многогранника этой плоскостью, должен быть задан не только многогранник, но и секущая плоскость. А построение плоскости сечения проходит в зависимости от задания этой плоскости. Основными способами задания плоскости, и в частности секущей плоскости, являются следующие:

тремя точками не лежащих на одной прямой;

прямой и не лежащей на ней точкой;

двумя параллельными прямыми;

двумя пересекающимися прямыми;

точкой и двумя скрещивающимися прямыми;

Возможны и другие способы задания секущей плоскости.

Поэтому все способы построения сечений многогранников можно разделить на методы.

Методы построения сечений многогранников

Метод сечений многогранников в стереометрии используется в задачах на построение. В его основе лежит умение строить сечение многогранника и определять вид сечения.

Существует три основных метода построения сечений многогранников:

Аксиоматический метод:

Метод следов.

Комбинированный метод.

Координатный метод.

Заметим , что метод следов и метод вспомогательных сечений являются разновидностями Аксиоматического метода построения сечений.

Можно также выделить следующие методы построения сечений многогранников:

построение сечения многогранника плоскостью, проходящей через заданную точку параллельно заданной плоскости;

построение сечения, проходящего через заданную прямую параллельно, другой заданной прямой;

построение сечения, проходящего через заданную точку параллельно двум заданным скрещивающимся прямым;

построение сечения многогранника плоскостью, проходящей через заданную прямую перпендикулярно заданной плоскости;

построение сечения многогранника плоскостью, проходящей через заданную точку перпендикулярно заданной прямой.

Основными действиями, составляющие методы построения сечений, являются нахождение точки пересечения прямой с плоскостью, построения линии пересечения двух плоскостей, построение прямой параллельной плоскости, перпендикулярной плоскости. Для построения прямой пересечения двух плоскостей обычно находят две ее точки и проводят через них прямую. Для построения точки пересечения прямой и плоскости находят в плоскости прямую, пересекающую данную. Тогда искомая точка получается в пересечении найденной прямой с данной.

Рассмотрим отдельно перечисленные нами методы построения сечений многогранников:

Метод следов.

Метод следов основывается (операеться) на аксиомах стереометрии, суть метода заключается в построении вспомогательной прямой, являющейся изображением линии пересечения секущей плоскости с плоскостью какой-либо грани фигуры. Удобнее всего строить изображение линии пересечения секущей плоскости с плоскостью нижнего основания. Эту линию называют основным следом секущей плоскости . Используя след, легко построить изображения точек секущей плоскости, находящихся на боковых ребрах или гранях фигуры. Последовательно соединяя образы этих точек, получим изображение искомого сечения.

Отметим, что при построении основного следа секущей плоскости используется следующее утверждение.

Если точки принадлежат секущей плоскости и не лежат на одной прямой, а их проекция (центральными или параллельными) на плоскость, выбранную в качестве основной, являются соответственно точки то точки пересечения соответственных прямых, то есть точки и лежат на одной прямой (рис.1, а, б).

рис.1.а рис.1.б

Эта прямая является основным следом секущей плоскости. Так как точки лежат на основном следе, то для его построения достаточно найти две точки из этих трех.

Метод вспомогательных сечений.

Этот метод построения сечений многогранников является в достаточной мере универсальным. В тех случаях, когда нужный след (или следы) секущей плоскости оказывается за пределами чертежа, этот метод имеет даже определенные преимущества. Вместе с тем следует иметь ввиду, что построения, выполняемые при использовании этого метода, зачастую получаются “скученными”. Тем не менее, в некоторых случаях метод вспомогательных сечений оказывается наиболее рациональным.

Комбинированный метод

Суть комбинированного метода построения сечений многогранников состоит в применении теорем о параллельности прямых и плоскостей в пространстве в сочетании с аксиоматическим методом.

Координатный метод построения сечений.

Суть координатного метода заключается в вычислении координат точек пересечения ребер или многогранника с секущей плоскостью, которая задается уравнением плоскости. Уравнение плоскости сечения вычисляется на основе условий задачи.

Заметим , что это способ построения сечения многогранника приемлем для компьютера, так как он связан с большим объемом вычислений и поэтому этот метод целесообразно реализовать с помощью ЭВМ.

Наша основная задача будет состоять в построении сечения многогранника с плоскостью, т.е. в построении пересечения этих двух множеств.

Построение сечений многогранников

Прежде всего заметим, что сечение выпуклого многогранника есть выпуклый плоский многоугольник, вершины которого в общем случае являются точками пересечения секущей плоскости с ребрами многогранника, а стороны с его гранями.

Примеры построения сечений:

Способы задания сечения весьма разнообразны. Наиболее распространенным из них является способ задания секущей плоскости тремя точками, не лежащими на одной прямой.

Пример 1. Для параллелепипеда ABCDA 1 B 1 C 1 D 1 . Построить сечение проходящее через точки M, N, L.

Решение:

Соединим точки M и L, лежащие в плоскости AA 1 D 1 D.

Пересечем прямую ML (принадлежащую сечению) с ребром A 1 D 1 1 D 1 D. Получим точку X 1 .

Точка X1 лежит на ребре A 1 D 1 , а значит и плоскости A 1 B 1 C 1 D 1 , соединим ее сточкой N, лежащей в этой же плоскости.

X 1 N пересекается с ребром A 1 B 1 в точке К.

Соединим точки K и M, лежащие в одной плоскости AA 1 B 1 B.

Найдем прямую пересечения плоскости сечения с плоскостью DD 1 C 1 C:

Пересечем прямую ML (принадлежащую сечению) с ребром DD 1 , они лежат в одной плоскости AA 1 D 1 D, получим точку X 2 .

Пересечем прямую KN (принадлежащую сечению) с ребром D 1 C 1 , они лежат в одной плоскости A 1 B 1 C 1 D 1 , получим точку X3;

Точки X2 и X3 лежат в плоскости DD 1 C 1 C. Проведем прямую X 2 X 3 , которая пересечет ребро C 1 C в точке T, а ребро DC в точке P. И соединим точки L и P, лежащие в плоскости ABCD.

Таким образом, задача считается решенной, если найдены все отрезки, по которым плоскость пересекает грани многогранника, что и мы сделали. MKNTPL - искомое сечение.

Заметим. Эту же самую задачу на построение сечения, можно решить воспользуевавшийся свойством параллельных плоскостей.

Из выше сказанного можно составить алгоритм (правило) решения задач, данного типа.

Правила построения сечений многогранников:

1. проводим прямые через точки, лежащие в одной плоскости;

   ищем прямые пересечения плоскости сечения с гранями многогранника, для этого:

Пример 2. D L , M

Решим аксиоматическим методом:

Проведем вспомогательную плоскость DKM , которая пересекает ребра АВ и ВС в точках Е и F (ход решение на рис 2.). Построим «след» КМ плоскости сечения на этой вспомогательной плоскости, найдем точку пересечения КМ и Е F – точку Р. Точка Р, как и L , лежит в плоскости АВС, и можно провести прямую, по которой плоскость сечения пересекает плоскость АВС(«след» сечения в плоскости АВС).

Пример 3. На ребрах AB и AD пирамиды MABCD зададим соответственно точки P и Q - середины этих ребер, а на ребре MC зададим точку R. Построим сечение пирамиды плоскостью, проходящей через точки P, Q и R.

Решение проведем комбинированным методом:

1). Ясно, что основным следом плоскости PQR является прямая PQ.

2). Найдем точку К, в которой плоскость МАС пересекает прямую PQ. Точки К и R принадлежат и плоскости PQR, и плоскости MAC. Поэтому, проведя прямую KR, мы получим линию пересечения этих плоскостей.

3). Найдем точку N=AC BD, проведем прямую MN и найдем точку F=KR MN.

4). Точка F является общей точкой плоскостей PQR и MDB, то есть эти плоскости пересекаются по прямой, проходящей через точку F. Вместе с тем так как PQ - средняя линия треугольника ABD, то PQ параллена BD, то есть прямая PQ параллельна и плоскости MDB. Тогда плоскость PQR, проходящая через прямую PQ, пересекает плоскость MDB по прямой, параллельной прямой PQ, то есть параллельной и прямой BD. Поэтому в плоскости MDB через точку F проведем прямую, параллельную прямой BD.

5). Дальнейшие построения понятны из рисунка. В итоге получаем многоугольник PQD"RB" - искомое сечение

Рассмотрим сечения призмы для простоты, то есть удобства логических размышлений рассмотрим сечения куба (рис.3.а):

Рис. 3.а

Сечения призмы плоскостями, параллельными боковым ребрам, является параллелограммами. В частности, параллелограммами являются диагональные сечения (рис. 4).

Опр. Диагональным сечением призмы называется сечение плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани.

Многоугольник, получающийся при диагональном сечении призмы, является параллелограммом. Вопрос о числе диагональных сечений n -угольной призмы труднее, чем вопрос о числе диагоналей. Сечений будет столько же сколько диагоналей у основания. Мы знаем, что у выпуклой призмы в основаниях – выпуклые многоугольники, а у выпуклого n -угольника диагоналей. И так можно говорить, что диагональных сечений вдвое меньше, чем диагоналей.

Заметим: При построении сечений параллелепипеда на рисунке следует учитывать тот факт, что если секущая плоскость пересекает две противоположные грани по каким – то отрезкам, то эти отрезки параллельны «по свойству параллелепипеда т.е. противоположные грани параллелепипеда параллельны и равны.»

Дадим ответы на часто возникающие вопросы:

Какие многоугольники получаются в сечении куба плоскостью?

«треугольник, четырехугольник, пятиугольник, шестиугольник ».

Может ли в сечении куба плоскостью получиться семиугольник? А восьмиугольник?

«не могут».

3)Возникает вопрос чему равно наибольшее число сторон многоугольника, полученного сечением многогранника с плоскостью?

Наибольшее число сторон многоугольника, полученного в сечении многогранника плоскостью, равно числу граней многогранника .

Пример 3. Построить сечение призмы A 1 B 1 C 1 D 1 ABCD плоскостью, проходящей через три точки M, N, K.

Рассмотрим случай расположения точек M, N, K на поверхности призмы (рис. 5).

Рассмотрим случай: В данном случае очевидно, что M1 = B1.

Построение:

Пример 4. Построить сечение параллелепипеда ABCDA 1 B 1 C 1 D 1 плоскостью, проходящей через точки M, N, P (точки указаны на чертеже (рис.6)).

Решение:

Рис. 6

Точки N и P лежат в плоскости сечения и в плоскости нижнего основания параллелепипеда. Построим прямую, проходящую через эти точки. Эта прямая является следом секущей плоскости на плоскость основания параллелепипеда.

Продолжим прямую, на которой лежит сторона AB параллелепипеда. Прямые AB и NP пересекутся в некоторой точке S. Эта точка принадлежит плоскости сечения.

Так как точка M также принадлежит плоскости сечения и пересекает прямую АА 1 в некоторой точке Х.

Точки X и N лежат в одной плоскости грани АА 1 D 1 D, соединим их и получим прямую XN.

Так как плоскости граней параллелепипеда параллельны, то через точку M можно провести прямую в грани A 1 B 1 C 1 D 1 , параллельную прямой NP. Эта прямая пересечет сторону В 1 С 1 в точке Y.

Аналогично проводим прямую YZ, параллельно прямой XN. Соединяем Z с P и получаем искомое сечение – MYZPNX.

Сечения пирамиды плоскостями, проходящими через ее вершину, представляют собой треугольники. В частности, треугольниками являются диагональные сечения. Это сечения плоскостями, проходящими через два не соседних боковых ребра пирамиды.

Пример 4. Построить сечение пирамиды АВС D плоскостью, проходящей через точки К, L , M .

Решение:

1. Проведем еще одну вспомогательную плоскость DCK и построим точку пересечения В L и D К – точку Е. Эта точка принадлежит обеим вспомогательным плоскостям (рис. 7, б);

   Найдем точку пересечения отрезков LM и ЕС (эти отрезки лежат в плоскости BLC , рис.7, в) – точку F . Точка F лежит в плоскости сечения и в плоскости DCK ;

   Проведем прямую KF и найдем точку пересечения этой прямой с DC – точку N (точка N принадлежит сечению). Четырехугольник KLNM – искомое сечение.

Этот же пример решим по другому .

Допустим что по точкам К, L , и М построено сечение KLNM (рис. 7). Обозначим через F точку пересечения диагоналей четырехугольника KLNM . Проведем прямую DF и обозначим через F 1 ее точку пересечения с гранью АВС. Точка F 1 совпадает с точкой пересечения прямых АМ и СК (F 1 одновременно принадлежит плоскостям АМ D и D СК). Точку F 1 легко построить. Далее строим точку F как точку пересечения DF 1 и LM . Далее находим точку N .

Рассмотренный прием называют методом внутреннего проектирования . (Для нашего случая речь идет о центральном проектировании. Четырехугольник K МСА есть проекция четырехугольника KMNL из точки D . При этом точка пересечения диагоналей KMNL – точка F – переходит в точку пересечения диагоналей четырехугольника K МСА – точку F 1 .

Площадь сечения многогранника.

Задача на вычисление площади сечения многогранника обычно решается в несколько этапов. Если в задаче говориться, что сечение построено (или что секущая плоскость проведена и т.п.), то на первом этапе решения выясняют вид фигуры полученной в сечении.

Это необходимо сделать, чтобы выбрать соответствующую формулу для вычисления площади сечения. После того как вид фигуры, полученной в сечении, выяснен и выбрана формула для подсчета площади этой фигуры, переходят непосредственно к вычислительной работе.

В некоторых случаях может оказаться проще, если, не выясняя вида фигуры, полученной в сечении, перейти сразу к вычислениям ее площади по формуле, которая следует из теоремы.

Теорема о площади ортогональной проекции многоугольника: площадь ортогональной проекции многоугольника на плоскость равна произведению его площади на косинус угла между плоскостью многоугольника и плоскостью проекции: .

Справедлива формула для вычисления площади сечения: где это площадь ортогональной проекции фигуры, полученной в сечении, аэто угол между секущей плоскостью и плоскостью, на которую фигура спроектирована. При таком ходе решения необходимо построить ортогональную проекцию фигуры, полученной в сечении, и подсчитать

Если в условии задачи говориться, что сечение требуется построить и найти площадь полученного сечения, то на первом этапе следует обосновано выполнить построение заданного сечения, и затем, естественно, определить вид фигуры, полученной в сечении, и т.д.

Отметим следующий факт: так как строятся сечения выпуклых многогранников, то многоугольник сечения будет тоже выпуклым, поэтому его площадь можно найти разбиением на треугольники, то есть площадь сечения равна сумме площадей треугольников из которых оно составлено.

Задача 1.

– правильная треугольная пирамида со стороной основания равной и высотой равной Постройте сечение пирамиды плоскостью, проходящей через точки, где – середина стороны, и найдите его площадь (рис.8).

Решение.

Сечением пирамиды является треугольник. Найдем его площадь.

Так как основание пирамиды – равносторонний треугольник и точка – середина стороны, то является высотой и тогда, .

Площадь треугольника можно найти:

Задача 2.

Боковое ребро правильной призмы равно стороне основания. Построить сечения призмы плоскостями, проходящими через точку A , перпендикулярно прямой Если найти площадь полученного сечения призмы.

Решение.

Построим заданное сечение. Сделаем это из чисто геометрических соображений, например, следующим образом.

В плоскости проходящей через заданную прямую и заданную точку проведем через эту точку прямую, перпендикулярную прямой (рис. 9). Воспользуемся с этой целью тем, что в треугольнике то есть его медиана является и высотой этого треугольника. Таким образом, прямая.

Через точку проведем еще одну прямую, перпендикулярную прямой. Проведем ее, например, в плоскости, проходящей через прямую. Ясно, что этой прямой является прямая

Итак, построены две пересекающиеся прямые, перпендикулярные прямой. Этими прямимы определяется плоскость, проходящая через точку перпендикулярно прямой то есть задана секущая плоскость.

Построим сечение призмы этой плоскостью. Заметим, что так как, то прямая параллельна плоскости. Тогда плоскость, проходящая через прямую, пересекает плоскость по прямой, параллельной прямой, то есть и прямой. Проведем через точку прямую и полученную точку соединим точкой.

Четырехугольник заданное сечение. Определим его площадь.

Понятно что четырехугольник является прямоугольником, то есть его площадь

рис. 9

Метод сечений многогранников в стереометрии используется в задачах на построение. В его основе лежит умение строить сечение многогранника и определять вид сечения.

Данный материал характеризуется следующим особенностями:

1. Метод сечений применяется только для многогранников, так как различные сложные (наклонные) виды сечений тел вращения не входят в программу средней школы.
2. В задачах используются в основном простейшие многогранники.
3. Задачи представлены в основном без числовых данных, чтобы создать возможность их многовариантного использования.

Чтобы решить задачу построения сечения многогранника ученик должен знать:

• что значит построить сечение многогранника плоскостью;
• как могут располагаться относительно друг друга многогранник и плоскость;
• как задается плоскость;
• когда задача на построение сечения многогранника плоскостью считается решенной.

Поскольку плоскость определяется:

• тремя точками;
• прямой и точкой;
• двумя параллельными прямыми;
• двумя пересекающимися прямыми,

построение плоскости сечения проходит в зависимости от задания этой плоскости. Поэтому все способы построения сечений многогранников можно разделить на методы.

Существует три основных метода построения сечений многогранников:

1. Метод следов.
2. Метод вспомогательных сечений.
3. Комбинированный метод.

Первые два метода являются разновидностями Аксиоматического метода построения сечений.

Можно также выделить следующие методы построения сечений многогранников:

• построение сечения многогранника плоскостью, проходящей через заданную точку параллельно заданной плоскости;
• построение сечения, проходящего через заданную прямую параллельно другой заданной прямой;
• построение сечения, проходящего через заданную точку параллельно двум заданным скрещивающимся прямым;
• построение сечения многогранника плоскостью, проходящей через заданную прямую перпендикулярно заданной плоскости;
• построение сечения многогранника плоскостью, проходящей через заданную точку перпендикулярно заданной прямой.

В федеральный перечень учебников по геометрии для 10-11 класов входят учебники авторов:

• Атанасяна Л.С., Бутузова В.Ф., Кадомцева С.Б. и др (Геометрия, 10-11);
• Погорелова А.В. (Геометрия, 7-11);
• Александрова А.Д., Вернера А.Л., Рыжик В.И. (Геометрия, 10-11);
• Смирновой И.М. (Геометрия, 10-11);
• Шарыгина И.Ф. (Геометрия, 10-11).

Рассмотрим подробнее учебники Л.С, Атанасяна и Погорелова А.В.

В учебнике Л.С. Атанасяна на тему “Построение сечений многогранников” выделено два часа. В 10 классе в теме “Параллельность прямых и плоскостей” после изучения тетраэдра и параллелепипеда отводится один час на изложение параграфа “Задачи на построение сечений”. Рассматриваются сечения тетраэдра и параллелепипеда. И тема “Параллельность прямых и плоскостей” завершается решением задач на одном или двух часах (всего задач на построение сечений в учебнике восемь).

В учебнике Погорелова А.В. на построение сечений отводится около трех часов в главе “Многогранники”: один – на изучение темы “Изображение призмы и построение ее сечений”, второй – на изучение темы “Построение пирамиды и ее плоских сечений” и третий – на решение задач. В списке задач, приведенных после темы, задач на сечение насчитывается всего около десяти.

Мы предлагаем систему уроков по теме “Построение сечений многогранников” для учебника Погорелова А.В.

Материал предлагается расположить в той последовательности, в какой он может применяться для обучения учащихся. Из изложения темы “Многогранники” предлагается исключить следующие параграфы: “Построение сечений призмы” и “Построение сечений пирамиды” с тем, чтобы систематизировать данный материал в конце этой темы “Многогранники”. Классифицировать его по тематике задач с примерным соблюдением принципа “от простого к сложному” можно весьма условно следующим образом:

1. Определение сечения многогранников.
2. Построение сечений призмы, параллелепипеда, пирамиды методом следов. (Как правило в школьном курсе стереометрии используются задачи на построение сечений многогранников, решаемые основными методами. Остальные методы, в связи с их более высоким уровнем сложности, учитель может оставить для рассмотрения на факультативных занятиях или на самостоятельное изучение. В задачах на построение основными методами требуется построить плоскость сечения, проходящую через три точки).
3. Нахождение площади сечений в многогранниках (без использования теоремы о площади ортогональной проекции многоугольника).
4. Нахождение площади сечений в многогранниках (с применением теоремы о площади ортогональной проекции многоугольника).

СТЕРЕОМЕТРИЧЕСКИЕ ЗАДАЧИ НА ПОСТРОЕНИЕ СЕЧЕНИЙ МНОГОГРАННИКОВ И МЕТОДИКА ИХ ИСПОЛЬЗОВАНИЯ НА УРОКАХ В 10-11 КЛАССАХ.

(система уроков и факультативных занятий по теме “Построение сечений многогранников”)

УРОК 1.

Тема урока: “Построение сечений многогранников”.

Цель урока: ознакомление с методами построений сечений многогранников.

Этапы урока:

1. Актуализация опорных знаний.
2. Постановка задачи.
3. Изучение нового материала:

А) Определение сечения.

Б) Методы построений сечений:

а) метод следов;

б) метод вспомогательных сечений;

в) комбинированный метод.

1. Закрепление материала.

Примеры построений сечений методом следов.

1. Подведение итогов урока.

Ход урока.

1. Актуализация опорных знаний.

Вспомним:
- пересечение прямой с плоскостью;
- пересечение плоскостей;
- свойства параллельных плоскостей.

2. Постановка задачи.

Вопросы к классу:
- Что значит построить сечение многогранника плоскостью?
- Как могут располагаться относительно друг друга многогранник и плоскость?
- Как задается плоскость?
- Когда задача на построение сечения многогранника плоскостью считается решенной?

3. Изучение нового материала.

А) Итак, задача состоит в построении пересечения двух фигур: многогранника и плоскости (рис.1). Это могут быть: пустая фигура (а), точка (б), отрезок (в), многоугольник (г). Если пересечение многогранника и плоскости есть многоугольник, то этот многоугольник называется сечением многогранника плоскостью.

Будем рассматривать только случай, когда плоскость пересекает многогранник по его внутренности. При этом пересечением данной плоскости с каждой гранью многогранника будет некоторый отрезок. Таким образом, задача считается решенной, если найдены все отрезки, по которым плоскость пересекает грани многогранника.

Исследуйте сечения куба (рис.2) и ответьте на следующие вопросы:

Какие многоугольники получаются в сечении куба плоскостью? (Важно число сторон многоугольника);

[ Предполагаемые ответы: треугольник, четырехугольник, пятиугольник, шестиугольник.]

Может ли в сечении куба плоскостью получиться семиугольник? А восьмиугольник и т.д.? Почему?

Давайте рассмотрим призму и ее возможные сечения плоскостью (на модели). Какие многоугольники получаются?

Какой можно сделать вывод? Чему равно наибольшее число сторон многоугольника, полученного сечением многогранника с плоскостью?

[ Наибольшее число сторон многоугольника, полученного в сечении многогранника плоскостью, равно числу граней многогранника.]

Б) а) Метод следов заключается в построении следов секущей плоскости на плоскость каждой грани многогранника. Построение сечения многогранника методом следов обычно начинают с построения так называемого основного следа секущей плоскости, т.е. следа секущей плоскости на плоскости основания многогранника.

б) Метод вспомогательных сечений построения сечений многогранников является в достаточной мере универсальным. В тех случаях, когда нужный след (или следы) секущей плоскости оказывается за пределами чертежа, этот метод имеет даже определенные преимущества. Вместе с тем следует иметь ввиду, что построения, выполняемые при использовании этого метода, зачастую получаются “скученными”. Тем не менее в некоторых случаях метод вспомогательных сечений оказывается наиболее рациональным.

Метод следов и метод вспомогательных сечений являются разновидностями аксиоматического метода построения сечений многогранников плоскостью.

в) Суть комбинированного метода построения сечений многогранников состоит в применении теорем о параллельности прямых и плоскостей в пространстве в сочетании с аксиоматическим методом.

А теперь на примере решения задач рассмотрим метод следов.

4. Закрепление материала.

Задача 1.

Построить сечение призмы ABCDA 1 B 1 C 1 D 1 плоскостью, проходящей через точки P, Q, R (точки указаны на чертеже (рис.3)).

Решение.

Рис. 3

1. Построим след секущей плоскости на плоскость нижнего основания призмы. Рассмотрим грань АА 1 В 1 В. В этой грани лежат точки сечения P и Q. Проведем прямую PQ.
2. Продолжим прямую PQ, которая принадлежит сечению, до пересечения с прямой АВ. Получим точку S 1 , принадлежащую следу.
3. Аналогично получаем точку S 2 пересечением прямых QR и BC.
4. Прямая S 1 S 2 - след секущей плоскости на плоскость нижнего основания призмы.
5. Прямая S 1 S 2 пересекает сторону AD в точке U, сторону CD в точке Т. Соединим точки P и U, так как они лежат в одной плоскости грани АА 1 D 1 D. Аналогично получаем TU и RT.
6. PQRTU – искомое сечение.

Построить сечение параллелепипеда ABCDA 1 B 1 C 1 D 1 плоскостью, проходящей через точки M, N, P (точки указаны на чертеже (рис.4)).

Решение.

1. Точки N и P лежат в плоскости сечения и в плоскости нижнего основания параллелепипеда. Построим прямую, проодящую через эти точки. Эта прямая является следом секущей плоскости на плоскость основания параллелепипеда.
2. Продолжим прямую, на которой лежит сторона AB параллелепипеда. Прямые AB и NP пересекутся в некоторой точке S. Эта точка принадлежит плоскости сечения.
3. Так как точка M также принадлежит плоскости сечения и пересекает прямую АА 1 в некоторой точке Х.
4. Точки X и N лежат в одной плоскости грани АА 1 D 1 D, соединим их и получим прямую XN.
5. Так как плоскости граней параллелепипеда параллельны, то через точку M можно провести прямую в грани A 1 B 1 C 1 D 1 , параллельную прямой NP. Эта прямая пересечет сторону В 1 С 1 в точке Y.
6. Аналогично проводим прямую YZ, параллельно прямой XN. Соединяем Z с P и получаем искомое сечение – MYZPNX.

Задача 3 (для самостоятельного решения).

Построить сечение тетраэдра DACB плоскостью, проходящей через точки M, N, P (точки указаны на чертеже (рис.5)).

5. Подведение итогов урока.

Ответьте на вопрос: являются ли закрашенные фигуры сечениями изображенных многогранников плоскостью PQR? И выполните правильное построение (рис. 6).

Вариант 1.

Вариант 2.

Тема урока: НАХОЖДЕНИЕ ПЛОЩАДИ СЕЧЕНИЯ.

Цель урока: познакомить со способами нахождения площади сечения многогранника.

Этапы урока:

1. Актуализация опорных знаний.

Вспомнить теорему о площади ортогональной проекции многоугольника.

2. Решение задач на нахождение площади сечения:

Без использования теоремы о площади ортогональной проекции многоугольника;

С использованием теоремы о площади ортогональной проекции многоугольника.

3. Подведение итогов урока.

Ход урока.

1. Актуализация опорных знаний.

Вспомним теорему о площади ортогональной проекции многоугольника: площадь ортогональной проекции многоугольника на плоскость равна произведению его площади на косинус угла между плоскостью многоугольника и плоскостью проекции.

2. Решение задач.

ABCD – правильная треугольная пирамида со стороной основания AB равной а и высотой DH равной h . Постройте сечение пирамиды плоскостью, проходящей через точки D, C и М, где М – середина стороны АВ, и найдите его площадь (рис.7).

Сечением пирамиды является треугольник MCD. Найдем его площадь.

S = 1/2 · DH · CM = 1/2 · =

Найти площадь сечения куба ABCDA 1 B 1 C 1 D 1 с ребром а плоскостью, проходящей через вершину D и точки Е и F на ребрах А 1 D 1 и C 1 D 1 соответственно, если A 1 E = k · D 1 E и C 1 F = k · D 1 F.

Построение сечения:

1. Поскольку точки Е и F принадлежат плоскости сечения и плоскости грани A 1 B 1 C 1 D 1 , а две плоскости пересекаются по прямой, то прямая EF будет являться следом секущей плоскости на плоскость грани A 1 B 1 C 1 D 1 (рис.8).
2. Аналогично получаются прямые ED и FD.
3. EDF – искомое сечение.

Задача 3 (для самостоятельного решения).

Построить сечение куба ABCDA 1 B 1 C 1 D 1 со стороной а плоскостью, проходящей через точки B, M и N, где Ь – середина ребра АА 1 , а N – середина ребра СС 1 .

Сечение строим методом следов.

Площадь сечения находим с помощью теоремы о площади ортогональной проекции многоугольника. Ответ: S = 1/2 · a 2 .