Пирамида 4 угла. Объем четырехугольной пирамиды. Что такое пирамида

Понятие многочлена

Определение многочлена: многочлен - это сумма одночленов. Пример многочлена:

здесь мы видим сумму двух одночленов, а это и есть многочлен, т.е. сумма одночленов.

Слагаемые, из которых состоит многочлен, называются членами многочлена.

Является ли разность одночленов многочленом? Да, является, ведь разность легко приводится к сумме, пример: 5a – 2b = 5a + (-2b).

Одночлены тоже считают многочленами. Но в одночлене нет суммы, тогда почему его считают многочленом? А к нему можно прибавить ноль и получить его сумму с нулевым одночленом. Итак, одночлен - это частный случай многочлена, он состоит из одного члена.

Число ноль - это нулевой многочлен.

Стандартный вид многочлена

Что такое многочлен стандартного вида? Многочлен есть сумма одночленов и если все эти одночлены, составляющие многочлен, записаны в стандартном виде, кроме того среди них не должно быть подобных, тогда многочлен записан в стандартном виде.

Пример многочлена в стандартном виде:

здесь многочлен состоит из 2-х одночленов, каждый из которых имеет стандартный вид, среди одночленов нет подобных.

Теперь пример многочлена, который не имеет стандартный вид:

здесь два одночлена: 2a и 4a являются подобными. Надо их сложить, тогда многочлен получит стандартный вид:

Ещё пример:

Этот многочлен приведен к стандартному виду? Нет, у него второй член не записан в стандартом виде. Записав его в стандартном виде, получаем многочлен стандартного вида:

Степень многочлена

Что такое степень многочлена?

Степень многочлена определение:

Степень многочлена - наибольшая степень, которую имеют одночлены, составляющие данный многочлен стандартного вида.

Пример. Какова степень многочлена 5h? Степень многочлена 5h равна одному, ведь в этот многочлен входит всего один одночлен и степень его равна одному.

Другой пример. Какова степень многочлена 5a 2 h 3 s 4 +1? Степень многочлена 5a 2 h 3 s 4 + 1 равна девяти, ведь в этот многочлен входят два одночлена, наибольшую степень имеет первый одночлен 5a 2 h 3 s 4 , а его степень равна 9-ти.

Ещё пример. Какова степень многочлена 5? Степень многочлена 5 равна нулю. Итак, степень многочлена, состоящего только из числа, т.е. без букв, равна нулю.

Последний пример. Какова степень нулевого многочлена, т.е. нуля? Степень нулевого многочлена не определена.

Среди различных выражений, которые рассматриваются в алгебре, важное место занимают суммы одночленов. Приведем примеры таких выражений:
\(5a^4 - 2a^3 + 0,3a^2 - 4,6a + 8 \)
\(xy^3 - 5x^2y + 9x^3 - 7y^2 + 6x + 5y - 2 \)

Сумму одночленов называют многочленом. Слагаемые в многочлене называют членами многочлена. Одночлены также относят к многочленам, считая одночлен многочленом, состоящим из одного члена.

Например, многочлен
\(8b^5 - 2b \cdot 7b^4 + 3b^2 - 8b + 0,25b \cdot (-12)b + 16 \)
можно упростить.

Представим все слагаемые в виде одночленов стандартного вида:
\(8b^5 - 2b \cdot 7b^4 + 3b^2 - 8b + 0,25b \cdot (-12)b + 16 = \)
\(= 8b^5 - 14b^5 + 3b^2 -8b -3b^2 + 16 \)

Приведем в полученном многочлене подобные члены:
\(8b^5 -14b^5 +3b^2 -8b -3b^2 + 16 = -6b^5 -8b + 16 \)
Получился многочлен, все члены которого являются одночленами стандартного вида, причем среди них нет подобных. Такие многочлены называют многочленами стандартного вида .

За степень многочлена стандартного вида принимают наибольшую из степеней его членов. Так, двучлен \(12a^2b - 7b \) имеет третью степень, а трехчлен \(2b^2 -7b + 6 \) - вторую.

Обычно члены многочленов стандартного вида, содержащих одну переменную, располагают в порядке убывания показателей ее степени. Например:
\(5x - 18x^3 + 1 + x^5 = x^5 - 18x^3 + 5x + 1 \)

Сумму нескольких многочленов можно преобразовать (упростить) в многочлен стандартного вида.

Иногда члены многочлена нужно разбить на группы, заключая каждую группу в скобки. Поскольку заключение в скобки - это преобразование, обратное раскрытию скобок, то легко сформулировать правила раскрытия скобок:

Если перед скобками ставится знак «+», то члены, заключаемые в скобки, записываются с теми же знаками.

Если перед скобками ставится знак «-», то члены, заключаемые в скобки, записываются с противоположными знаками.

Преобразование (упрощение) произведения одночлена и многочлена

С помощью распределительного свойства умножения можно преобразовать (упростить) в многочлен произведение одночлена и многочлена. Например:
\(9a^2b(7a^2 - 5ab - 4b^2) = \)
\(= 9a^2b \cdot 7a^2 + 9a^2b \cdot (-5ab) + 9a^2b \cdot (-4b^2) = \)
\(= 63a^4b - 45a^3b^2 - 36a^2b^3 \)

Произведение одночлена и многочлена тождественно равно сумме произведений этого одночлена и каждого из членов многочлена.

Этот результат обычно формулируют в виде правила.

Чтобы умножить одночлен на многочлен, надо умножить этот одночлен на каждый из членов многочлена.

Мы уже неоднократно использовали это правило для умножения на сумму.

Произведение многочленов. Преобразование (упрощение) произведения двух многочленов

Вообще, произведение двух многочленов тождественно равно сумме произведении каждого члена одного многочлена и каждого члена другого.

Обычно пользуются следующим правилом.

Чтобы умножить многочлен на многочлен, надо каждый член одного многочлена умножить на каждый член другого и сложить полученные произведения.

Формулы сокращенного умножения. Квадраты суммы, разности и разность квадратов

С некоторыми выражениями в алгебраических преобразованиях приходится иметь дело чаще, чем с другими. Пожалуй, наиболее часто встречаются выражения \((a + b)^2, \; (a - b)^2 \) и \(a^2 - b^2 \), т. е. квадрат суммы, квадрат разности и разность квадратов. Вы заметили, что названия указанных выражений как бы не закончены, так, например, \((a + b)^2 \) - это, конечно, не просто квадрат суммы, а квадрат суммы а и b. Однако квадрат суммы а и b встречается не так уж часто, как правило, вместо букв а и b в нем оказываются различные, иногда довольно сложные выражения.

Выражения \((a + b)^2, \; (a - b)^2 \) нетрудно преобразовать (упростить) в многочлены стандартного вида, собственно, вы уже встречались с таким заданием при умножении многочленов:
\((a + b)^2 = (a + b)(a + b) = a^2 + ab + ba + b^2 = \)
\(= a^2 + 2ab + b^2 \)

Полученные тождества полезно запомнить и применять без промежуточных выкладок. Помогают этому краткие словесные формулировки.

\((a + b)^2 = a^2 + b^2 + 2ab \) - квадрат суммы равен сумме квадратов и удвоенного произведения.

\((a - b)^2 = a^2 + b^2 - 2ab \) - квадрат разности равен сумме квадратов без удвоенного произведения.

\(a^2 - b^2 = (a - b)(a + b) \) - разность квадратов равна произведению разности на сумму.

Эти три тождества позволяют в преобразованиях заменять свои левые части правыми и обратно - правые части левыми. Самое трудное при этом - увидеть соответствующие выражения и понять, чем в них заменены переменные а и b. Рассмотрим несколько примеров использования формул сокращенного умножения.

• апофема — высота боковой грани правильной пирамиды , которая проведена из ее вершины (кроме того, апофемой является длина перпендикуляра, который опущен из середины правильного многоугольника на 1-ну из его сторон);
• боковые грани (ASB, BSC, CSD, DSA) — треугольники, которые сходятся в вершине;
• боковые ребра ( AS , BS , CS , DS ) — общие стороны боковых граней;
• вершина пирамиды (т. S) — точка, которая соединяет боковые ребра и которая не лежит в плоскости основания;
• высота ( SO ) — отрезок перпендикуляра, который проведен через вершину пирамиды к плоскости ее основания (концами такого отрезка будут вершина пирамиды и основание перпендикуляра);
• диагональное сечение пирамиды — сечение пирамиды, которое проходит через вершину и диагональ основания;
• основание (ABCD) — многоугольник, которому не принадлежит вершина пирамиды.

Свойства пирамиды.

1. Когда все боковые ребра имеют одинаковую величину, тогда:

• около основания пирамиды легко описать окружность , при этом вершина пирамиды будет проецироваться в центр этой окружности;
• боковые ребра образуют с плоскостью основания одинаковые углы ;
• кроме того, верно и обратное, т.е. когда боковые ребра образуют с плоскостью основания равные углы, либо когда около основания пирамиды можно описать окружность и вершина пирамиды будет проецироваться в центр этой окружности, значит, все боковые ребра пирамиды имеют одинаковую величину.

2. Когда боковые грани имеют угол наклона к плоскости основания одной величины, тогда:

• около основания пирамиды легко описать окружность, при этом вершина пирамиды будет проецироваться в центр этой окружности;
• высоты боковых граней имеют равную длину;
• площадь боковой поверхности равняется ½ произведения периметра основания на высоту боковой грани.

3. Около пирамиды можно описать сферу в том случае, если в основании пирамиды лежит многоугольник, вокруг которого можно описать окружность (необходимое и достаточное условие). Центром сферы станет точка пересечения плоскостей, которые проходят через середины ребер пирамиды перпендикулярно им. Из этой теоремы делаем вывод, что как около всякой треугольной, так и около всякой правильной пирамиды можно описать сферу.

4. В пирамиду можно вписать сферу в том случае, если биссекторные плоскости внутренних двугранных углов пирамиды пересекаются в 1-ной точке (необходимое и достаточное условие). Эта точка станет центром сферы.

Простейшая пирамида.

По количеству углов основания пирамиды делят на треугольные, четырехугольные и так далее.

Пирамида будет треугольной , четырехугольной , и так далее, когда основанием пирамиды будет треугольник, четырехугольник и так далее. Треугольная пирамида есть четырехгранник — тетраэдр . Четырехугольная — пятигранник и так далее.

Четырехугольной пирамидой называется многогранник, в основании которого лежит квадрат, а все боковые грани являются одинаковыми равнобедренными треугольниками.

У данного многогранника есть множество различных свойств:

• Его боковые ребра и прилегающие к ним двугранные углы равны между собой;
• Площади боковых граней одинаковы;
• В основании правильной четырехугольной пирамиды лежит квадрат;
• Высота, опущенная из вершины пирамиды, пересекается с точкой пересечения диагоналей основания.

Все эти свойства помогают легко находить . Однако довольно часто помимо нее требуется рассчитать объем многогранника. Для этого применяется формула объема четырехугольной пирамиды:

То есть объем пирамиды равен одной третьей произведения высоты пирамиды на площадь основания. Так как равна произведению его равных сторон, то мы сразу вписываем в выражение объема формулу площади квадрата.
Рассмотрим пример расчета объема четырехугольной пирамиды.

Пусть дана четырехугольная пирамида, в основании которой лежит квадрат со стороной a = 6 см. Боковая грань пирамиды равна b = 8 см. Найдите объем пирамиды.

Чтобы найти объем заданного многогранника, нам потребуется длина его высоты. Поэтому мы найдем ее, применив теорему Пифагора. Для начала рассчитаем длину диагонали. В синем треугольнике она будет гипотенузой. Стоит также помнить, что диагонали квадрата равны между собой и в точке пересечения делятся пополам:


Теперь из красного треугольника найдем необходимую нам высоту h . Она будет равна:

Подставим необходимые значения и найдем высоту пирамиды:

Теперь, зная высоту, можем подставлять все значения в формулу объема пирамиды и рассчитывать необходимую величину:

Вот таким образом, зная несколько простых формул, мы смогли рассчитать объем правильной четырехугольной пирамиды. Не забывайте, что данная величина измеряется в кубических единицах.

Площадь поверхности пирамиды. В этой статье мы рассмотрим с вами задачи с правильными пирамидами. Напомню, что правильная пирамида – это пирамида, основанием которой является правильный многоугольник, вершина пирамиды проецируется в центр этого многоугольника.

Боковая грань такой пирамиды это равнобедренный треугольник. Высота этого треугольника, проведенная из вершины правильной пирамиды, называется апофемой, SF – апофема:

В представленном ниже типе задач требуется найти площадь поверхности всей пирамиды или площадь её боковой поверхности. На блоге уже рассмотрено несколько задач с правильными пирамидами, где ставился вопрос о нахождении элементов (высоты, ребра основания, бокового ребра), .

В заданиях ЕГЭ, как правило, рассматриваются правильные треугольные, четырёхугольные и шестиугольные пирамиды. Задач с правильными пятиугольными и семиугольными пирамидами не встречал.

Формула площади всей поверхности проста — требуется найти сумму площади основания пирамиды и площади её боковой поверхности:

Рассмотрим задачи:

Стороны основания правильной четырехугольной пирамиды равны 72, боковые ребра равны 164. Найдите площадь поверхности этой пирамиды.

Площадь поверхности пирамиды равна сумме площадей боковой поверхности и основания:

*Боковая поверхность состоит из четырёх равных по площади треугольников. Основание пирамиды это квадрат.

Площадь боковой стороны пирамиды можем вычислить воспользовавшись :

Таким образом, площадь поверхности пирамиды равна:

Ответ: 28224

Стороны основания правильной шестиугольной пирамиды равны 22, боковые ребра равны 61. Найдите площадь боковой поверхности этой пирамиды.

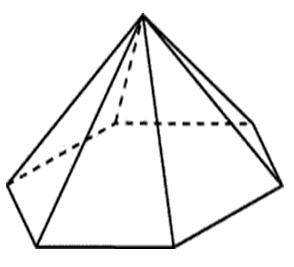
Основанием правильной шестиугольной пирамиды является правильный шестиугольник.

Площадь боковой поверхности данной пирамиды состоит из шести площадей равных треугольников с сторонами 61,61 и 22:

Найдём площадь треугольника, воспользуемся формулой Герона:

Таким образом, площадь боковой поверхности равна:

Ответ: 3240

*В представленных выше задачах площадь боковой грани можно было найти используя другую формулу треугольника, но для этого нужно вычислить апофему.

27155. Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 6 и высота равна 4.

Для того, чтобы найти площадь поверхности пирамиды нам необходимо знать площадь основания и площадь боковой поверхности:

Площадь основания равна 36, так как это квадрат со стороной 6.

Боковая поверхность состоит из четырёх граней, которые являются равными треугольниками. Для того, чтобы найти площадь такого треугольника требуется знать его основание и высоту (апофему):

*Площадь треугольника равна половине произведения основания и высоты проведённой к этому основанию.

Основание известно, оно равно шести. Найдём высоту. Рассмотрим прямоугольный треугольник (он выделен жёлтым):

Один катет равен 4, так как это высота пирамиды, другой равен 3, так как он равен половине ребра основания. Можем найти гипотенузу, по теореме Пифагора:

Значит площадь боковой поверхности пирамиды равна:

Таким образом, площадь поверхности всей пирамиды равна:

Ответ: 96

27069. Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.

27070. Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды.

Существуют ещё формулы площади боковой поверхности правильной пирамиды. В правильной пирамиде основание является ортогональной проекцией боковой поверхности, поэтому:

P - периметр основания, l - апофема пирамиды

*Эта формула основывается на формуле площади треугольника.

Если хотите узнать подробнее как эти формулы выводятся, не пропустите, следите за публикацией статей. На этом всё. Успеха Вам!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.