مختصات قطبی مختصات کارتزین
یک سیستم مختصات مستطیلی در یک صفحه توسط دو محور مختصات متقابل عمود بر X'X و Y'Y تشکیل می شود. محورهای مختصات در نقطه O که مبدأ نامیده می شود قطع می شوند، جهت مثبت محورها (در یک سیستم مختصات سمت راست) انتخاب می شود تا زمانی که محور X'X می چرخد. در خلاف جهت عقربه های ساعت 90 درجه، جهت مثبت آن با جهت مثبت محور Y'Y منطبق است. چهار زاویه (I، II، III، IV) که توسط محورهای مختصات X'X و Y'Y تشکیل شده اند، زوایای مختصات نامیده می شوند (شکل 1 را ببینید).
موقعیت نقطه A در صفحه با دو مختصات x و y تعیین می شود. مختصات x برابر طول قطعه OB، مختصات y برابر طول قطعه OC در واحدهای اندازه گیری انتخاب شده است. بخشهای OB و OC با خطوطی که از نقطه A موازی با محورهای Y'Y و X'X ترسیم میشوند، تعریف میشوند. مختصات x را ابسیسا نقطه A و مختصات y را مختصات نقطه A می نامند که به صورت زیر نوشته می شود: A(x,y).
اگر نقطه A در زاویه مختصات I قرار داشته باشد، نقطه A دارای ابسیسا و مختصات مثبت است. اگر نقطه A در زاویه مختصات II قرار داشته باشد، نقطه A دارای یک ابسیسا منفی و یک مختصات مثبت است. اگر نقطه A در زاویه مختصات III قرار گیرد، نقطه A دارای ابسیسا و مختصات منفی است. اگر نقطه A در زاویه مختصات IV قرار گیرد، نقطه A دارای یک ابسیسا مثبت و یک مختصات منفی است.
سیستم مختصات مستطیلی در فضاتوسط سه محور مختصات عمود بر یکدیگر OX، OY و OZ تشکیل شده است. محورهای مختصات در نقطه O که مبدا نامیده می شود قطع می شوند، در هر محور یک جهت مثبت انتخاب می شود که با فلش ها نشان داده می شود و واحد اندازه گیری قطعات روی محورها نشان داده می شود. واحدهای اندازه گیری برای همه محورها یکسان است. OX - محور ابسیسا، OY - محور ارتین، OZ - محور کاربردی. جهت مثبت محورها طوری انتخاب می شود که وقتی محور OX در خلاف جهت عقربه های ساعت 90 درجه می چرخد، اگر این چرخش از جهت مثبت محور OZ مشاهده شود، جهت مثبت آن با جهت مثبت محور OY منطبق شود. چنین سیستم مختصاتی را راست دست می نامند. اگر شست دست راست به عنوان جهت X، انگشت اشاره به عنوان جهت Y و انگشت وسط به عنوان جهت Z در نظر گرفته شود، سیستم مختصات راست دست تشکیل می شود. انگشتان مشابه دست چپ سیستم مختصات چپ را تشکیل می دهند. ترکیب سیستم مختصات راست و چپ به طوری که محورهای مربوطه بر هم منطبق شوند غیرممکن است (شکل 2 را ببینید).

موقعیت نقطه A در فضا با سه مختصات x، y و z تعیین می شود. مختصات x برابر طول قطعه OB، مختصات y طول قطعه OC، مختصات z طول قطعه OD در واحدهای اندازه گیری انتخاب شده است. بخش های OB، OC و OD به ترتیب توسط صفحاتی که از نقطه A موازی با صفحات YOZ، XOZ و XOY ترسیم می شوند، تعریف می شوند. مختصات x را ابسیسا نقطه A، مختصات y را مختصات نقطه A، مختصات z را مصداق نقطه A می نامند که به صورت زیر نوشته می شود: A(a, b, c).
اورتی
یک سیستم مختصات مستطیلی (از هر بعد) نیز با مجموعه ای از بردارهای واحد که با محورهای مختصات تراز شده اند توصیف می شود. تعداد بردارهای واحد برابر با بعد دستگاه مختصات است و همگی بر یکدیگر عمود هستند.
در حالت سه بعدی، چنین بردارهای واحدی معمولاً نشان داده می شوند من j کیا هایکس ه y ه z. در این مورد، در مورد یک سیستم مختصات راست دست، فرمول های زیر با حاصلضرب بردارها معتبر است:
- [من j]=ک ;
- [j ک]=من ;
- [ک من]=j .
داستان
سیستم مختصات مستطیلی اولین بار توسط رنه دکارت در اثر خود "گفتار در مورد روش" در سال 1637 معرفی شد. بنابراین، سیستم مختصات مستطیلی نیز نامیده می شود - سیستم مختصات دکارتی. روش مختصات توصیف اجسام هندسی آغاز هندسه تحلیلی بود. پیر فرما نیز به توسعه روش مختصات کمک کرد، اما آثار او برای اولین بار پس از مرگش منتشر شد. دکارت و فرما از روش مختصات فقط در هواپیما استفاده کردند.
روش مختصات برای فضای سه بعدی اولین بار توسط لئونارد اویلر در قرن هجدهم مورد استفاده قرار گرفت.
همچنین ببینید
پیوندها
بنیاد ویکی مدیا 2010.
- سیستم مختصات دکارتی
- درجه دکارتی
ببینید «مختصات دکارتی» در فرهنگهای دیگر چیست:
مختصات کارتزینی- (سیستم مختصات دکارتی) یک سیستم مختصات در یک صفحه یا در فضا، معمولاً با محورهای متقابل عمود بر هم و مقیاس های مساوی در امتداد محورها. به نام R. Descartes ... فرهنگ لغت دایره المعارفی بزرگ
مختصات کارتزین- یک سیستم مختصات متشکل از دو محور عمود بر هم. موقعیت یک نقطه در چنین سیستمی با استفاده از دو عدد که فاصله از مرکز مختصات را در امتداد هر یک از محورها تعیین می کند، تشکیل می شود. موضوعات اطلاع رسانی...... راهنمای مترجم فنی
مختصات کارتزین- (سیستم مختصات دکارتی)، سیستم مختصات در یک صفحه یا در فضا، معمولاً با محورهای متقابل عمود بر هم و مقیاس های مساوی در امتداد محورها. به نام R. Descartes ... فرهنگ لغت دایره المعارفی
مختصات کارتزین- Dekarto koordinatės statusas T sritis Standartizacija ir metrologija apibrėžtis Tiesinė plokštumos arba erdvės koordinačių sistema. Joje ašių masteliai paprastai būna lygūs. atitikmenys: انگلیسی. مختصات دکارتی vok. Kartesische Koordinaten، f… Penkiakalbis aiškinamasis metrologijos terminų žodynas
مختصات کارتزین- Dekarto koordinatės statusas T sritis fizika atitikmenys: engl. مختصات کارتزین؛ مختصات شبکه vok. kartesische Koordinaten، f rus. مختصات دکارتی، f pranc. coordonnées cartésiennes, f … Fizikos terminų žodynas
مختصات کارتزینی- روشی برای تعیین موقعیت نقاط روی صفحه با فاصله آنها تا دو محور مستقیم عمود بر هم. این مفهوم قبلاً در ارشمیدس و آپولوگیس پرگا بیش از دو هزار سال پیش و حتی در میان مصریان باستان دیده شده است. برای اولین بار این...... دایره المعارف ریاضی
مختصات کارتزینی- سیستم مختصات دکارتی [به نام فرانسوی ها. فیلسوف و ریاضیدان R. Descartes (R. Descartes; 1596 1650)]، یک سیستم مختصات در یک صفحه یا در فضا، معمولا با محورهای متقابل عمود بر یکدیگر و مقیاس های مساوی در امتداد محورهای مستطیلی D ... فرهنگ لغت بزرگ دایره المعارفی پلی تکنیک
مختصات کارتزینی- (سیستم مختصات دکارتی)، سیستم مختصاتی در یک صفحه یا در فضا، معمولاً با محورهای متقابل عمود بر هم و مقیاس های مساوی در امتداد محورهای مستطیلی به نام R. Descartes. علوم طبیعی. فرهنگ لغت دایره المعارفی
مختصات کارتزینی- سیستمی برای قرار دادن هر نقطه ای که روی استخوان ها نسبت به دو محور که در زوایای قائم متقاطع هستند. این سیستم که توسط رنه دکارت ابداع شد، مبنایی برای روشهای استاندارد برای نمایش گرافیکی دادهها شد. خط افقی… … فرهنگ لغت توضیحی روانشناسی
مختصات- مختصات در هواپیما (چپ) و در فضا (راست). مختصات (از لاتین co together و ordinatus ordered)، اعدادی که موقعیت یک نقطه را روی یک خط مستقیم، صفحه، سطح، در فضا تعیین می کنند. مختصات فاصله هستند... فرهنگ لغت دایره المعارف مصور
مختصات قطبی
شماره تماس گرفته می شود شعاع قطبینقطه یا اولین مختصات قطبی. فاصله نمی تواند منفی باشد، بنابراین شعاع قطبی هر نقطه برابر است. اولین مختصات قطبی نیز با یک حرف یونانی ("rho") نشان داده می شود، اما من به نسخه لاتین عادت دارم و در آینده از آن استفاده خواهم کرد.
شماره تماس گرفته می شود زاویه قطبینقطه داده شده یا مختصات قطبی دوم. زاویه قطبی معمولاً در داخل (به اصطلاح) متفاوت است مقادیر زاویه اصلی). با این حال، استفاده از محدوده کاملاً قابل قبول است و در برخی موارد نیاز مستقیم به در نظر گرفتن تمام مقادیر زاویه از صفر تا "بی نهایت" وجود دارد. به هر حال، توصیه میکنم به اندازهگیری رادیان یک زاویه عادت کنید، زیرا کار کردن با درجه در ریاضیات بالاتر بهعنوان comme il faut در نظر گرفته نمیشود.
زن و شوهر نامیده می شود مختصات قطبینقطه ها پیدا کردن معانی خاص آنها آسان است. مماس یک زاویه تند مثلث قائم الزاویه، نسبت ضلع مقابل به ضلع مجاور است: بنابراین، خود زاویه: ![]() . طبق قضیه فیثاغورث، مجذور هیپوتانوس برابر است با مجموع مربع های پاها: , که به معنای شعاع قطبی است:
. طبق قضیه فیثاغورث، مجذور هیپوتانوس برابر است با مجموع مربع های پاها: , که به معنای شعاع قطبی است:
بدین ترتیب، ![]() .
.
یک پنگوئن خوب است، اما یک گله بهتر است: 
گوشه هایی با جهت گیری منفی ![]() در صورتی که برخی از خوانندگان هنوز از این جهت گیری اطلاعی نداشتند، آن را با فلش ها علامت گذاری کردم. در صورت تمایل، می توانید 1 دور (رادی یا 360 درجه) به هر یک از آنها "پیچ" کنید و به هر حال راحت باشید. مقادیر جدول:
در صورتی که برخی از خوانندگان هنوز از این جهت گیری اطلاعی نداشتند، آن را با فلش ها علامت گذاری کردم. در صورت تمایل، می توانید 1 دور (رادی یا 360 درجه) به هر یک از آنها "پیچ" کنید و به هر حال راحت باشید. مقادیر جدول:
اما نقطه ضعف این زوایای «سنتی» این است که بیش از حد (بیش از 180 درجه) در خلاف جهت عقربههای ساعت «پیچیده» میشوند. من این سوال را پیشبینی میکنم: "چرا یک نقطه ضعف وجود دارد و اصلاً چرا برخی زوایای منفی لازم است؟" در ریاضیات کوتاه ترین و منطقی ترین مسیرها ارزش گذاری می شود. خوب، از نقطه نظر فیزیک، جهت چرخش اغلب از اهمیت اساسی برخوردار است - هر یک از ما سعی کردیم با کشیدن دستگیره در جهت اشتباه در را باز کنیم =)
ترتیب و تکنیک ساختن نقاط در مختصات قطبی
تصاویر زیبا زیبا هستند، اما ساختن آنها در یک سیستم مختصات قطبی کار نسبتاً پر زحمتی است. با نقاطی که زوایای قطبی آنها هستند هیچ مشکلی وجود ندارد ![]() ، در مثال ما اینها نکات هستند
، در مثال ما اینها نکات هستند ![]() ; مقادیری که مضرب 45 درجه هستند نیز مشکل خاصی ایجاد نمی کنند: . اما چگونه می توان مثلاً یک نقطه را به درستی و با شایستگی ساخت؟
; مقادیری که مضرب 45 درجه هستند نیز مشکل خاصی ایجاد نمی کنند: . اما چگونه می توان مثلاً یک نقطه را به درستی و با شایستگی ساخت؟
شما به یک تکه کاغذ شطرنجی، یک مداد و ابزارهای طراحی زیر نیاز دارید: خط کش، قطب نما، نقاله. به عنوان آخرین راه، می توانید تنها با یک خط کش یا حتی ... بدون آن از پس آن برآیید! به ادامه مطلب بروید و مدرک دیگری دریافت خواهید کرد که این کشور شکست ناپذیر است =)
مثال 1
یک نقطه در سیستم مختصات قطبی بسازید.
اول از همه، شما باید درجه اندازه گیری زاویه را دریابید. اگر گوشه ناآشنا است یا شک دارید، بهتر است همیشه از آن استفاده کنید جدولیا یک فرمول کلی برای تبدیل رادیان به درجه. بنابراین زاویه ما (یا) است.
بیایید یک سیستم مختصات قطبی رسم کنیم (به ابتدای درس مراجعه کنید) و یک نقاله برداریم. صاحبان یک ساز گرد هیچ مشکلی برای علامت گذاری 240 درجه نخواهند داشت، اما به احتمال زیاد نسخه نیم دایره ای از دستگاه را روی دستان خود خواهید داشت. مشکل عدم وجود کامل نقاله در حضور چاپگر و قیچی با کاردستی حل شد.
دو راه وجود دارد: ورق را برگردانید و 120 درجه علامت بزنید یا نیم چرخش را پیچ کنید و به زاویه مخالف نگاه کنید. بیایید روش بزرگسالان را انتخاب کنیم و علامت 60 درجه بگذاریم: 
یا نقاله لیلیپوتی، یا قفس غول پیکر =) با این حال، برای اندازه گیری زاویه، مقیاس مهم نیست.
با استفاده از یک مداد، یک خط مستقیم نازک از قطب و علامت ایجاد شده بکشید: 
ما زاویه را مرتب کردیم، حالا شعاع قطبی بعدی است. یک قطب نما بگیرید و در امتداد خطما راه حل آن را روی 3 واحد تنظیم می کنیم، البته اغلب این، سانتی متر است: 
حالا سوزن را با دقت روی میله قرار می دهیم و با یک حرکت چرخشی یک بریدگی کوچک (رنگ قرمز) ایجاد می کنیم. نقطه مورد نیاز ساخته شد: 
می توانید بدون قطب نما با اعمال خط کش مستقیماً روی خط مستقیم ساخته شده و اندازه گیری 3 سانتی متر انجام دهید. اما همانطور که بعدا خواهیم دید، در مسائل مربوط به ساخت و ساز در یک سیستم مختصات قطبییک موقعیت معمولی زمانی است که باید دو یا چند نقطه را با شعاع قطبی یکسان علامت گذاری کنید، بنابراین سخت کردن فلز کارآمدتر است. به طور خاص، در نقاشی ما، با چرخش پایه قطب نما 180 درجه، به راحتی می توان یک بریدگی دوم ایجاد کرد و یک نقطه متقارن نسبت به قطب ایجاد کرد. بیایید از آن برای کار کردن با مطالب پاراگراف بعدی استفاده کنیم:
رابطه بین سیستم مختصات مستطیلی و قطبی
به طور مشخص بیایید اضافه کنیمبه سیستم مختصات قطبی، یک شبکه مختصات "منظم" و یک نقطه در نقاشی بکشید: 
هنگام ترسیم مختصات قطبی، همیشه مفید است که این ارتباط را در نظر داشته باشید. هر چند خواه ناخواه خود را بدون هیچ اشاره ای نشان می دهد.
بیایید با استفاده از مثال یک نقطه خاص رابطه بین مختصات قطبی و دکارتی را برقرار کنیم. مثلث قائم الزاویه ای را در نظر بگیرید که در آن هیپوتنوس برابر با شعاع قطبی است: و پاهای آن برابر با مختصات "X" و "Y" نقطه در سیستم مختصات دکارتی است: ![]() .
.
سینوس یک زاویه حاد نسبت طرف مقابل به هیپوتنوز است: ![]()
کسینوس یک زاویه حاد نسبت پای مجاور به هیپوتونوس است: ![]()
در عین حال تعاریف سینوس، کسینوس (و تانژانت کمی زودتر) را از برنامه درسی پایه نهم مدرسه جامع تکرار کردیم.
لطفاً فرمول های کاری را در کتاب مرجع خود اضافه کنید که مختصات دکارتی یک نقطه را از طریق مختصات قطبی آن بیان می کند - ما باید بیش از یک بار با آنها برخورد کنیم و دفعه بعد همین الان =)
بیایید مختصات یک نقطه را در یک سیستم مختصات مستطیلی پیدا کنیم: 
بدین ترتیب:
فرمولهای بهدستآمده، حفره دیگری را در مسئله ساختوساز باز میکنند، زمانی که اصلاً میتوانید بدون نقاله این کار را انجام دهید: ابتدا مختصات دکارتی نقطه را پیدا میکنیم (البته در پیشنویس)، سپس به صورت ذهنی مکان مورد نظر را روی نقشه پیدا میکنیم و این نکته را علامت بزنید در مرحله آخر یک خط مستقیم نازک می کشیم که از نقطه ساخته شده و قطب می گذرد. در نتیجه، معلوم می شود که ظاهراً زاویه با نقاله اندازه گیری شده است.
خندهدار است که دانشآموزان بسیار ناامید حتی میتوانند بدون خطکش انجام دهند و به جای آن از لبه صاف کتاب درسی، دفتر یا کتاب نمره استفاده کنند - بالاخره سازندگان نوتبوک به معیارهای اندازهگیری، 1 مربع = 5 میلیمتر توجه کردند.
همه اینها مرا به یاد یک جوک معروف انداخت که در آن خلبانان مدبر مسیری را در امتداد یک بسته بلومور ترسیم کردند =) اگرچه به کنار شوخی، این شوخی چندان دور از واقعیت نیست، به یاد دارم که در یکی از پروازهای داخلی روسیه فدراسیون، همه ابزار ناوبری در هواپیما از کار افتاد و خدمه با موفقیت هواپیما را با استفاده از یک لیوان آب معمولی فرود آوردم که زاویه هواپیما را نسبت به زمین نشان می داد. و فرودگاه - اینجاست که از شیشه جلو قابل مشاهده است.
با استفاده از قضیه فیثاغورث ذکر شده در ابتدای درس، به راحتی می توان فرمول های معکوس را بدست آورد: , بنابراین:

خود زاویه "phi" به طور استاندارد از طریق مماس قطبی بیان می شود - کاملاً مشابه آرگومان عدد مختلطبا تمام مشکلاتش
همچنین توصیه می شود گروه دوم فرمول ها را در چمدان مرجع خود قرار دهید.
پس از توضیح مفصل با نکات جداگانه، اجازه دهید به ادامه طبیعی موضوع بپردازیم:
معادله یک خط در مختصات قطبی
اساساً معادله یک خط در یک سیستم مختصات قطبی است تابع شعاع قطبی از زاویه قطبی (برهان). در این مورد، زاویه قطبی در نظر گرفته می شود در رادیان(!) و به طور مداوممقادیر را از تا می گیرد (گاهی اوقات باید آن را تا بی نهایت در نظر گرفت، یا در تعدادی از مشکلات برای راحتی از تا). هر مقدار از زاویه "phi" که در آن گنجانده شده است دامنهتابع، مربوط به یک مقدار واحد از شعاع قطبی است.
عملکرد قطبی را می توان با نوعی رادار مقایسه کرد - زمانی که یک پرتو نوری که از یک قطب تابیده می شود در خلاف جهت عقربه های ساعت می چرخد و یک خط را "تشخیص" (کشش) می کند.
یک مثال استاندارد از منحنی قطبی است مارپیچ ارشمیدسی. تصویر زیر او را نشان می دهد دور اول- وقتی شعاع قطبی زیر زاویه قطبی مقادیری از 0 تا: 
علاوه بر این، با عبور از محور قطبی در نقطه، مارپیچ به باز شدن ادامه میدهد و بینهایت دورتر از قطب حرکت میکند. اما چنین مواردی در عمل بسیار نادر است. یک وضعیت معمولی تر زمانی است که در تمام چرخش های بعدی ما "در همان خطی" که در محدوده به دست آمده است راه می رویم.
در مثال اول با مفهوم مواجه می شویم حوزه تعریفتابع قطبی: از آنجایی که شعاع قطبی غیر منفی است، در اینجا نمی توان زوایای منفی را در نظر گرفت.
! توجه داشته باشید : در برخی موارد مرسوم است که استفاده شود مختصات قطبی تعمیم یافته، که در آن شعاع می تواند منفی باشد و کمی بعد به طور خلاصه این رویکرد را بررسی خواهیم کرد
علاوه بر مارپیچ ارشمیدس، بسیاری از منحنی های معروف دیگر نیز وجود دارد، اما، همانطور که می گویند، شما نمی توانید از هنر به اندازه کافی لذت ببرید، بنابراین من نمونه هایی را انتخاب کردم که اغلب در کارهای عملی واقعی یافت می شوند.
ابتدا ساده ترین معادلات و ساده ترین خطوط:
یک معادله شکل، معادله ای را که از قطب خارج می شود، مشخص می کند اشعه. در واقع، در مورد آن فکر کنید، اگر مقدار زاویه همیشه(هر چیزی که "er" باشد) به طور مداوم، پس چه خطی است؟
توجه داشته باشید : در سیستم مختصات قطبی تعمیم یافته، این معادله خط مستقیمی را که از قطب می گذرد تعریف می کند
یک معادله فرم تعیین می کند... اولین بار حدس بزنید - اگر برای هرکسشعاع زاویه "فی" ثابت می ماند؟ در واقع این تعریف است دایرهمرکز در قطب شعاع .
مثلا، . برای وضوح، معادله این خط را در یک سیستم مختصات مستطیلی پیدا می کنیم. با استفاده از فرمول به دست آمده در پاراگراف قبل، جایگزینی را انجام می دهیم:
بیایید هر دو طرف را مربع کنیم:
– معادله یک دایرهبا مرکز در مبدا شعاع 2، که باید بررسی شود.
از زمان ایجاد و انتشار مقاله در مورد وابستگی خطی و استقلال خطی بردارهاچندین نامه از بازدیدکنندگان سایت دریافت کردم که سؤالی با این روحیه پرسیدند: "یک سیستم مختصات مستطیلی ساده و راحت وجود دارد، چرا ما به یک مورد مورب دیگر نیاز داریم؟" پاسخ ساده است: ریاضیات تلاش می کند همه چیز و همه را در آغوش بگیرد! علاوه بر این، در یک موقعیت معین، راحتی مهم است - همانطور که می بینید، به دلیل سادگی بیش از حد معادله، کار با دایره در مختصات قطبی بسیار سودآورتر است.
و گاهی اوقات یک مدل ریاضی اکتشافات علمی را پیش بینی می کند. بنابراین ، در یک زمان رئیس دانشگاه کازان N.I. لوباچفسکی به شدت ثابت شده است، از طریق یک نقطه دلخواه از هواپیما می توان ترسیم کرد بی نهایت خطوط مستقیم، به موازات این یکی. در نتیجه، او مورد بدنام تمام دنیای علمی قرار گرفت، اما ... هیچ کس نتوانست این واقعیت را رد کند. تنها یک قرن بعد، ستاره شناسان دریافتند که نور در فضا در امتداد مسیرهای منحنی حرکت می کند، جایی که هندسه غیر اقلیدسی لوباچفسکی، که به طور رسمی مدت ها قبل از این کشف توسط او ایجاد شده بود، شروع به کار می کند. فرض بر این است که این ویژگی خود فضا است که انحنای آن به دلیل فاصله های کوچک (با استانداردهای نجومی) برای ما نامرئی است.
بیایید وظایف ساخت و ساز معنی دارتری را در نظر بگیریم:
مثال 2
یک خط بسازید
راه حل: اول از همه بیایید پیدا کنیم دامنه. از آنجایی که شعاع قطبی غیرمنفی است، نابرابری باید برقرار باشد. شما می توانید قوانین مدرسه را برای حل نابرابری های مثلثاتی به خاطر بسپارید، اما در موارد ساده مانند این، من یک روش حل سریع تر و بصری تر را توصیه می کنم:
یک نمودار کسینوس را تصور کنید. اگر هنوز در حافظه شما ثبت نشده است، آن را در صفحه پیدا کنید نمودارهای توابع ابتدایی. نابرابری به ما چه می گوید؟ به ما می گوید که نمودار کسینوس باید قرار گیرد نه کمترمحور آبسیسا و این در بخش اتفاق می افتد. و بر این اساس، فاصله مناسب نیست.
بنابراین، دامنه تعریف تابع ما این است: ، یعنی نمودار در سمت راست قطب قرار دارد (در اصطلاح سیستم دکارتی - در نیمه صفحه سمت راست).
در مختصات قطبی، اغلب یک ایده مبهم وجود دارد که کدام خط یک معادله خاص را تعریف می کند، بنابراین برای ساختن آن، باید نقاطی را که به آن تعلق دارند پیدا کنید - و هر چه بیشتر، بهتر. معمولاً آنها به ده یا دو (یا حتی کمتر) محدود می شوند. البته ساده ترین راه این است که بگیرید مقادیر زاویه جدول. برای وضوح بیشتر، یک نوبت به مقادیر منفی "پیچ" می کنم: 
به دلیل برابری کسینوس ![]() مقادیر مثبت مربوطه نیازی به شمارش مجدد ندارند:
مقادیر مثبت مربوطه نیازی به شمارش مجدد ندارند: 
بیایید یک سیستم مختصات قطبی را به تصویر بکشیم و نقاط پیدا شده را رسم کنیم، در حالی که ترسیم همان مقادیر "er" در یک زمان راحت است، و با استفاده از فناوری مورد بحث در بالا، بریدگی های جفتی با قطب نما ایجاد می کنیم: 
در اصل، خط به وضوح ترسیم شده است، اما برای تایید کامل حدس، اجازه دهید معادله آن را در سیستم مختصات دکارتی پیدا کنیم. می توانید فرمول های اخیراً مشتق شده را اعمال کنید ![]() ، اما من یک ترفند حیله گرانه تر را به شما می گویم. ما به طور مصنوعی هر دو طرف معادله را در "er" ضرب می کنیم: و از فرمول های انتقال فشرده تر استفاده می کنیم:
، اما من یک ترفند حیله گرانه تر را به شما می گویم. ما به طور مصنوعی هر دو طرف معادله را در "er" ضرب می کنیم: و از فرمول های انتقال فشرده تر استفاده می کنیم:
با جداسازی یک مربع کامل، معادله خط را به شکل قابل تشخیص در می آوریم: 
![]() – معادله یک دایرهبا مرکز در نقطه، شعاع 2.
– معادله یک دایرهبا مرکز در نقطه، شعاع 2.
از آنجایی که طبق شرایط فقط لازم بود ساخت و ساز انجام شود و تمام است ، نقاط پیدا شده را به آرامی با یک خط به هم وصل می کنیم: 
آماده. اشکالی ندارد اگر کمی ناهموار باشد، لازم نیست بدانید که دایره بوده است ;-)
چرا مقادیر زاویه را خارج از بازه در نظر نگرفتیم؟ پاسخ ساده است: فایده ای ندارد. به دلیل تناوب بودن تابع، با یک حرکت بی پایان در امتداد دایره ساخته شده مواجه می شویم.
به راحتی می توان یک تحلیل ساده انجام داد و به این نتیجه رسید که یک معادله شکل دایره ای با قطر را با مرکز در نقطه مشخص می کند. به بیان تصویری ، همه این دایره ها روی محور قطبی "نشسته" و لزوماً از قطب عبور می کنند. با این حال، اگر شرکت شاد به سمت چپ حرکت کند - به ادامه محور قطبی (به این فکر کنید که چرا).
یک کار مشابه برای حل به تنهایی:
مثال 3
یک خط بسازید و معادله آن را در یک سیستم مختصات مستطیلی پیدا کنید.
اجازه دهید روند حل مشکل را سیستماتیک کنیم:
اول از همه، ما دامنه تعریف تابع را می یابیم که بررسی آن راحت است سینوسیفوراً بفهمید که سینوس کجا غیر منفی است.
در مرحله دوم با استفاده از مختصات قطبی نقاط را محاسبه می کنیم مقادیر زاویه جدول; تجزیه و تحلیل کنید که آیا امکان کاهش تعداد محاسبات وجود دارد؟
در مرحله سوم نقاط سیستم مختصات قطبی را رسم می کنیم و با دقت آنها را با خط به هم وصل می کنیم.
و در نهایت معادله خط را در دستگاه مختصات دکارتی می یابیم.
نمونه راه حل در پایان درس است.
ما الگوریتم کلی و تکنیک ساخت را در مختصات قطبی توضیح می دهیم
و سرعت قابل توجهی را افزایش دهددر قسمت دوم سخنرانی، اما قبل از آن با یک خط مشترک دیگر آشنا می شویم:
رز قطبی
درست است، ما در مورد یک گل با گلبرگ صحبت می کنیم:
مثال 4
خطوطی را که توسط معادلات در مختصات قطبی داده می شود بسازید
دو روش برای ساخت گل رز قطبی وجود دارد. ابتدا، با فرض اینکه شعاع قطبی نمی تواند منفی باشد، مسیر پیچ خورده را دنبال می کنیم:
راه حل:
الف) دامنه تعریف تابع را پیدا می کنیم: ![]()
این نابرابری مثلثاتی نیز به راحتی قابل حل است: از مواد مقاله تبدیل هندسی نمودارهامشخص است که اگر آرگومان یک تابع دو برابر شود، نمودار آن 2 برابر به محور مختصات کوچک می شود. لطفا نمودار تابع را در مثال اول این درس پیدا کنید. این سینوسی بالای محور x کجا قرار دارد؟ در فواصل زمانی ![]() . در نتیجه، نابرابری توسط بخش های مربوطه ارضا می شود، و دامنهعملکرد ما:
. در نتیجه، نابرابری توسط بخش های مربوطه ارضا می شود، و دامنهعملکرد ما: ![]() .
.
به طور کلی، راه حل نابرابری های مورد بررسی، اتحاد تعداد نامتناهی از بخش ها است، اما، دوباره، ما فقط به یک دوره علاقه مندیم.
شاید برای برخی از خوانندگان استفاده از یک روش تحلیلی برای یافتن دامنه تعریف آسانتر باشد. ما قطع می کنیم به قسمت های مساویو اول از همه مرزهای قطعه اول را پیدا کنید. ما چنین استدلال می کنیم: سینوس غیر منفی است, چه زمانی استدلال او از 0 تا راد متغیر است. شامل. در مثال ما: . با تقسیم تمام قسمت های نابرابری مضاعف بر 2، بازه لازم را بدست می آوریم:
اکنون شروع به "برش قطعات مساوی 90 درجه" در خلاف جهت عقربه های ساعت می کنیم:
- بخش یافت شده، البته، در حوزه تعریف گنجانده شده است.
- فاصله بعدی - شامل نمی شود.
- بخش بعدی - شامل؛
– و در نهایت، فاصله – گنجانده نشده است.
درست مثل دیزی - "دوست دارد، دوست ندارد، دوست دارد، دوست ندارد" =) با این تفاوت که در اینجا فال گیری وجود ندارد. بله، این فقط نوعی عشق به روش چینی است….
بنابراین، ![]() و خط نشان دهنده یک گل رز با دو گلبرگ یکسان است. کشیدن طرح به صورت شماتیک کاملاً امکان پذیر است ، اما بسیار توصیه می شود که به درستی پیدا و علامت گذاری شود بالای گلبرگ ها. رئوس مطابقت دارند نقاط میانی بخش های حوزه تعریف، که در این مثال مختصات زاویه ای آشکاری دارند
و خط نشان دهنده یک گل رز با دو گلبرگ یکسان است. کشیدن طرح به صورت شماتیک کاملاً امکان پذیر است ، اما بسیار توصیه می شود که به درستی پیدا و علامت گذاری شود بالای گلبرگ ها. رئوس مطابقت دارند نقاط میانی بخش های حوزه تعریف، که در این مثال مختصات زاویه ای آشکاری دارند ![]() . که در آن طول گلبرگهستند:
. که در آن طول گلبرگهستند: 
در اینجا نتیجه طبیعی یک باغبان دلسوز است: 
لازم به ذکر است که طول گلبرگ را می توان به راحتی از معادله مشاهده کرد - زیرا سینوس محدود است: ، بنابراین حداکثر مقدار "er" مطمئناً از دو تجاوز نخواهد کرد.
ب) خط داده شده توسط معادله را بسازیم. بدیهی است که طول گلبرگ این گل رز نیز دو است، اما قبل از هر چیز به حوزه تعریف علاقه مندیم. بیایید روش تحلیلی "برش" را اعمال کنیم: سینوس وقتی که آرگومانش باشد غیر منفی استدر محدوده صفر تا پی است، در این مورد: . تمام قسمت های نابرابری را بر 3 تقسیم می کنیم و اولین بازه را بدست می آوریم:
در مرحله بعد، «تکهکردن پای» را با راد شروع میکنیم. (60 درجه):
- بخش وارد دامنه تعریف می شود.
– فاصله – شامل نخواهد شد.
- بخش - مناسب خواهد بود؛
– فاصله – شامل نخواهد شد.
- بخش - مناسب خواهد بود؛
– فاصله – شامل نخواهد شد.
این فرآیند در 360 درجه با موفقیت انجام می شود.
بنابراین، دامنه تعریف عبارت است از: ![]() .
.
اعمالی که به طور کلی یا جزئی انجام می شود به راحتی قابل انجام ذهنی است.
ساخت و ساز. اگر در پاراگراف قبلی همه چیز با زوایای راست و زوایای 45 درجه به خوبی انجام شد، در اینجا باید کمی سرهم بندی کنید. بیایید پیدا کنیم بالای گلبرگ ها. طول آنها از همان ابتدای کار قابل مشاهده بود. 
لطفاً توجه داشته باشید که بین بالای گلبرگ ها باید فضاهای مساوی وجود داشته باشد، در این مورد 120 درجه.
توصیه می شود نقاشی را در بخش های 60 درجه (که با خطوط سبز مشخص شده اند) علامت گذاری کنید و جهت بالای گلبرگ ها (خطوط خاکستری) را بکشید. راحت است که رئوس خود را با استفاده از قطب نما علامت گذاری کنید - یک بار فاصله 2 واحدی را اندازه گیری کنید و سه بریدگی در جهت های ترسیم شده 30، 150 و 270 درجه ایجاد کنید: 
آماده. من درک می کنم که این یک کار مشکل ساز است، اما اگر می خواهید همه چیز را عاقلانه ترتیب دهید، باید وقت بگذارید.
اجازه دهید یک فرمول کلی را فرموله کنیم: معادله ای از شکل، یک عدد طبیعی است)، یک گل رز قطبی را تعریف می کند که طول گلبرگ آن برابر است.
به عنوان مثال، معادله یک چهار برگ با طول گلبرگ 5 واحد را مشخص می کند، معادله یک گل رز 5 گلبرگ با طول گلبرگ 3 واحد را مشخص می کند. و غیره.
دستورالعمل ها
اگر نمی توانید از ماشین حساب استفاده کنید، اما به اینترنت دسترسی دارید، عملیات ریاضی را به صورت متنی یادداشت کنید و آنها را در قسمت جستجوی جستجو در صفحه اصلی وب سایت گوگل وارد کنید. این موتور جستجو دارای یک ماشین حساب چند منظوره داخلی است که استفاده از آن بسیار ساده تر از هر موتور دیگری است. هیچ رابطی با دکمه ها وجود ندارد - تمام داده ها باید به صورت متنی در یک فیلد وارد شوند. مثلاً اگر معلوم باشد مختصاتنقاط افراطی بخشدر یک سیستم مختصات سه بعدی A(51.34 17.2 13.02) و A(-11.82 7.46 33.5)، سپس مختصاتنقطه میانی بخش C((51.34-11.82)/2 (17.2+7.46)/2 (13.02+33.5)/2). با وارد کردن (51.34-11.82)/2 در قسمت عبارت جستجو، سپس (17.2+7.46)/2 و (13.02+33.5)/2، می توانید از Google برای دریافت استفاده کنید. مختصات C(19.76 12.33 23.26).
معادله استاندارد یک دایره به شما امکان می دهد چندین اطلاعات مهم در مورد این شکل پیدا کنید، به عنوان مثال، مختصات مرکز آن، طول شعاع. در برخی از مسائل، برعکس، شما نیاز به ایجاد یک معادله با استفاده از پارامترهای داده شده دارید.

دستورالعمل ها
بر اساس وظیفه ای که به شما داده شده است، مشخص کنید که چه اطلاعاتی در مورد دایره دارید. به یاد داشته باشید که هدف نهایی تعیین مختصات مرکز و همچنین قطر است. تمام اقدامات شما باید در جهت دستیابی به این نتیجه خاص باشد.
از داده ها در مورد وجود نقاط تقاطع با خطوط مختصات یا خطوط دیگر استفاده کنید. لطفا توجه داشته باشید که اگر دایره از محور آبسیسا عبور کند، دایره دوم دارای مختصات 0 و اگر از محور مختصات عبور کند، دایره اول خواهد بود. این مختصات به شما امکان می دهد مختصات مرکز دایره را بیابید و شعاع را نیز محاسبه کنید.
ویژگی های اساسی سکنت ها و مماس ها را فراموش نکنید. به ویژه، مفیدترین قضیه این است که در نقطه تماس شعاع و مماس یک زاویه قائمه تشکیل می دهند. اما لطفاً توجه داشته باشید که ممکن است از شما خواسته شود که تمام قضایای استفاده شده در طول دوره را اثبات کنید.
استانداردترین انواع را حل کنید تا بیاموزید که چگونه از داده های خاص برای معادله یک دایره استفاده کنید. بنابراین، علاوه بر مشکلات ذکر شده با مختصات مستقیم داده شده و مواردی که در آنها اطلاعاتی در مورد وجود نقاط تقاطع داده می شود، برای تدوین معادله یک دایره، می توانید از دانش مرکز دایره، طول دایره استفاده کنید. وتر و این وتر بر روی آن نهفته است.
برای حل یک مثلث متساوی الساقین بسازید که قاعده آن وتر داده شده و اضلاع مساوی آن شعاع باشد. کامپایل که از آن به راحتی می توانید داده های لازم را پیدا کنید. برای این کار کافی است از فرمول یافتن طول یک قطعه در یک صفحه استفاده کنید.
ویدیو در مورد موضوع
دایره به شکل شکلی شناخته می شود که از نقاط زیادی در صفحه ای با فاصله مساوی از مرکز آن تشکیل شده است. فاصله از مرکز تا نقاط دایرهشعاع نامیده می شود.

سیستم منظم متشکل از دو یا سه محور متقاطع عمود بر یکدیگر با مبدأ مشترک (منشا مختصات) و یک واحد طول مشترک نامیده می شود. سیستم مختصات دکارتی مستطیلی .
سیستم مختصات دکارتی عمومی (سیستم مختصات افین) ممکن است لزوماً شامل محورهای عمودی نباشد. به افتخار ریاضیدان فرانسوی رنه دکارت (1596-1662)، دقیقاً چنین سیستم مختصاتی نامگذاری شده است که در آن یک واحد طول مشترک در همه محورها اندازه گیری می شود و محورها مستقیم هستند.
سیستم مختصات دکارتی مستطیلی در یک هواپیما دارای دو محور و سیستم مختصات دکارتی مستطیلی در فضا - سه محور هر نقطه در یک صفحه یا در فضا با مجموعه منظمی از مختصات - اعداد مربوط به واحد طول سیستم مختصات - تعریف می شود.
توجه داشته باشید که همانطور که از تعریف بر می آید، یک سیستم مختصات دکارتی در یک خط مستقیم، یعنی در یک بعد وجود دارد. معرفی مختصات دکارتی بر روی یک خط یکی از روش هایی است که هر نقطه از یک خط را با یک عدد واقعی کاملاً مشخص، یعنی یک مختصات مرتبط می کند.
روش مختصات، که در آثار رنه دکارت به وجود آمد، نشانگر یک بازسازی انقلابی در تمام ریاضیات بود. تفسیر معادلات جبری (یا نابرابری ها) در قالب تصاویر هندسی (نمودار) و برعکس، جستجوی راه حل برای مسائل هندسی با استفاده از فرمول های تحلیلی و سیستم های معادلات امکان پذیر شد. بله، نابرابری z < 3 геометрически означает полупространство, лежащее ниже плоскости, параллельной координатной плоскости xOyو در بالای این هواپیما توسط 3 واحد واقع شده است.
با استفاده از سیستم مختصات دکارتی، عضویت یک نقطه در یک منحنی معین با این واقعیت مطابقت دارد که اعداد ایکسو yبرآورده کردن برخی از معادله بنابراین، مختصات یک نقطه روی یک دایره با مرکز در یک نقطه معین ( آ; ب) معادله را برآورده کنید (ایکس - آ)² + ( y - ب)² = آر² .
سیستم مختصات دکارتی مستطیلی در یک هواپیما
دو محور عمود بر صفحه ای با مبدأ مشترک و واحد مقیاس یکسان تشکیل می شوند سیستم مختصات مستطیلی دکارتی در هواپیما . یکی از این محورها محور نام دارد گاو نر، یا محور x ، دیگری - محور اوه، یا محور y . به این محورها، محورهای مختصات نیز می گویند. اجازه دهید با نشان دادن مایکسو مyبه ترتیب، طرح یک نقطه دلخواه مدر محور گاو نرو اوه. چگونه می توان پیش بینی ها را دریافت کرد؟ از نکته بگذریم م گاو نر. این خط مستقیم محور را قطع می کند گاو نردر نقطه مایکس. از نکته بگذریم مخط مستقیم عمود بر محور اوه. این خط مستقیم محور را قطع می کند اوهدر نقطه مy. این در تصویر زیر نشان داده شده است.
ایکسو yنکته ها مبر این اساس مقادیر بخش های هدایت شده را فراخوانی می کنیم OMایکسو OMy. مقادیر این بخش های هدایت شده بر این اساس محاسبه می شود ایکس = ایکس0 - 0 و y = y0 - 0 . مختصات کارتزین ایکسو yنکته ها م اوکیسا و ترتیب . این واقعیت که نقطه ممختصات دارد ایکسو y، به صورت زیر نشان داده می شود: م(ایکس, y) .
محورهای مختصات هواپیما را به چهار تقسیم می کنند ربع که شماره گذاری آن در شکل زیر نشان داده شده است. همچنین ترتیب علائم مختصات نقاط را بسته به موقعیت آنها در یک ربع خاص نشان می دهد.
علاوه بر مختصات مستطیلی دکارتی در یک صفحه، سیستم مختصات قطبی نیز اغلب در نظر گرفته می شود. در مورد روش انتقال از یک سیستم مختصات به دیگری - در درس سیستم مختصات قطبی .

سیستم مختصات دکارتی مستطیلی در فضا
مختصات دکارتی در فضا در قیاس کامل با مختصات دکارتی در صفحه معرفی شده است.
سه محور متقابل عمود بر هم در فضا (محورهای مختصات) با مبدأ مشترک Oو با همان مقیاس واحد تشکیل می دهند سیستم مختصات مستطیلی دکارتی در فضا .
یکی از این محورها محور نام دارد گاو نر، یا محور x ، دیگری - محور اوه، یا محور y ، سوم - محور اوز، یا محور اعمال می شود . اجازه دهید مایکس, مy مz- پیش بینی یک نقطه دلخواه مفضای روی محور گاو نر , اوهو اوزبه ترتیب.
از نکته بگذریم م گاو نرگاو نردر نقطه مایکس. از نکته بگذریم مصفحه عمود بر محور اوه. این صفحه محور را قطع می کند اوهدر نقطه مy. از نکته بگذریم مصفحه عمود بر محور اوز. این صفحه محور را قطع می کند اوزدر نقطه مz.

مختصات مستطیلی دکارتی ایکس , yو zنکته ها مبر این اساس مقادیر بخش های هدایت شده را فراخوانی می کنیم OMایکس, OMyو OMz. مقادیر این بخش های هدایت شده بر این اساس محاسبه می شود ایکس = ایکس0 - 0 , y = y0 - 0 و z = z0 - 0 .
مختصات کارتزین ایکس , yو zنکته ها مبر این اساس نامیده می شوند اوکیسا , ترتیب و اعمال کنید .
محورهای مختصاتی که به صورت جفت گرفته شده اند در صفحات مختصات قرار دارند xOy , yOzو zOx .
مسائل مربوط به نقاط در سیستم مختصات دکارتی
مثال 1.
آ(2; -3) ;
ب(3; -1) ;
سی(-5; 1) .
مختصات برآمدگی این نقاط را روی محور آبسیسا بیابید.
راه حل. همانطور که از قسمت تئوری این درس بر می آید، طرح ریزی یک نقطه بر روی محور آبسیسا روی خود محور آبسیسا، یعنی محور قرار دارد. گاو نر، و بنابراین دارای یک ابسیسا برابر با آبسیسا خود نقطه و یک مختصات (مختصات روی محور) است. اوه، که محور x آن را در نقطه 0 قطع می کند) که برابر با صفر است. بنابراین مختصات زیر را از این نقاط در محور x بدست می آوریم:
آx(2;0);
بx(3;0);
سیx (-5; 0).
مثال 2.در سیستم مختصات دکارتی، نقاط روی صفحه داده می شود
آ(-3; 2) ;
ب(-5; 1) ;
سی(3; -2) .
مختصات برآمدگی این نقاط را بر روی محور ارتین پیدا کنید.
راه حل. همانطور که از قسمت تئوری این درس بر می آید، طرح ریزی یک نقطه بر روی محور ترتیبی بر روی خود محور ترتیبی، یعنی محور قرار دارد. اوهو بنابراین دارای یک ترتیب برابر با مختصات خود نقطه و یک ابسیسا (مختصات روی محور) است. گاو نر، که محور ارتین آن را در نقطه 0 قطع می کند) که برابر با صفر است. بنابراین مختصات زیر را از این نقاط در محور ارتین بدست می آوریم:
آy (0;2);
بy (0;1);
سیy (0;-2).
مثال 3.در سیستم مختصات دکارتی، نقاط روی صفحه داده می شود
آ(2; 3) ;
ب(-3; 2) ;
سی(-1; -1) .
گاو نر .
گاو نر گاو نر گاو نر، دارای ابسیسا یکسان با نقطه داده شده، و یک مجرا از نظر قدر مطلق با ترتیب نقطه داده شده، و در مقابل علامت خواهد داشت. بنابراین مختصات زیر را از نقاط متقارن با این نقاط نسبت به محور بدست می آوریم گاو نر :
آ"(2; -3) ;
ب"(-3; -2) ;
ج"(-1; 1) .
خودتان مسائل را با استفاده از سیستم مختصات دکارتی حل کنید و سپس به راه حل ها نگاه کنید
مثال 4.تعیین کنید که در کدام ربع (چهارم، ترسیم با ربع - در انتهای بند "سیستم مختصات دکارتی مستطیلی در یک صفحه") یک نقطه می تواند قرار گیرد م(ایکس; y) ، اگر
1) xy > 0 ;
2) xy < 0 ;
3) ایکس − y = 0 ;
4) ایکس + y = 0 ;
5) ایکس + y > 0 ;
6) ایکس + y < 0 ;
7) ایکس − y > 0 ;
8) ایکس − y < 0 .
مثال 5.در سیستم مختصات دکارتی، نقاط روی صفحه داده می شود
آ(-2; 5) ;
ب(3; -5) ;
سی(آ; ب) .
مختصات نقاط متقارن با این نقاط را نسبت به محور پیدا کنید اوه .
بیایید با هم به حل مشکلات ادامه دهیم
مثال 6.در سیستم مختصات دکارتی، نقاط روی صفحه داده می شود
آ(-1; 2) ;
ب(3; -1) ;
سی(-2; -2) .
مختصات نقاط متقارن با این نقاط را نسبت به محور پیدا کنید اوه .
راه حل. 180 درجه حول محور بچرخانید اوهبخش جهت دار از محور اوهتا این نقطه. در شکل، جایی که ربع های صفحه نشان داده شده است، می بینیم که نقطه متقارن با نقطه داده شده نسبت به محور است. اوه، دارای همان ترتیب نقطه داده شده و یک ابسیسا از نظر قدر مطلق برابر با ابسیسا نقطه داده شده و مقابل علامت است. بنابراین مختصات زیر را از نقاط متقارن با این نقاط نسبت به محور بدست می آوریم اوه :
آ"(1; 2) ;
ب"(-3; -1) ;
ج"(2; -2) .
مثال 7.در سیستم مختصات دکارتی، نقاط روی صفحه داده می شود
آ(3; 3) ;
ب(2; -4) ;
سی(-2; 1) .
مختصات نقاط متقارن با این نقاط را نسبت به مبدا پیدا کنید.
راه حل. قطعه جهت دار را که از مبدا به نقطه داده شده می رود 180 درجه حول مبدا می چرخانیم. در شکلی که ربع های صفحه نشان داده شده است، می بینیم که نقطه ای متقارن با نقطه داده شده نسبت به مبدأ مختصات، دارای یک ابسیسا و اردیتی برابر با ابسیسا و ارتکاب نقطه داده شده است، اما مقابل علامت بنابراین مختصات زیر را از نقاط متقارن با این نقاط نسبت به مبدا بدست می آوریم:
آ"(-3; -3) ;
ب"(-2; 4) ;
سی(2; -1) .
مثال 8.
آ(4; 3; 5) ;
ب(-3; 2; 1) ;
سی(2; -3; 0) .
مختصات پیش بینی این نقاط را بیابید:
1) در هواپیما اکسی ;
2) در هواپیما Oxz ;
3) به هواپیما اویز ;
4) در محور آبسیسا؛
5) در محور ترتیبی؛
6) در محور کاربردی.
1) طرح ریزی یک نقطه بر روی یک صفحه اکسیبر روی خود این صفحه قرار دارد و بنابراین دارای یک ابسیسا و یک مجمل برابر با ابسیسا و مختص یک نقطه معین و یک اطلاق برابر با صفر است. بنابراین مختصات زیر را از پیش بینی های این نقاط به دست می آوریم اکسی :
آxy (4; 3; 0);
بxy (-3; 2; 0);
سیxy(2;-3;0).
2) طرح ریزی یک نقطه بر روی یک صفحه Oxzدر خود این صفحه قرار دارد و بنابراین دارای یک ابسیسا و اطلاق برابر با ابسیسا و اطلاق یک نقطه معین و یک مصداق برابر با صفر است. بنابراین مختصات زیر را از پیش بینی های این نقاط به دست می آوریم Oxz :
آxz (4; 0; 5);
بxz (-3; 0; 1);
سیxz (2; 0; 0).
3) طرح ریزی یک نقطه بر روی یک صفحه اویزبر روی خود این صفحه قرار دارد و بنابراین دارای یک ارتین و اطلاق برابر با مصداق و یک نقطه داده شده و یک ابسیسا برابر با صفر است. بنابراین مختصات زیر را از پیش بینی های این نقاط به دست می آوریم اویز :
آyz(0; 3; 5);
بyz (0; 2; 1);
سیyz (0; -3; 0).
4) همانطور که از قسمت تئوری این درس بر می آید، طرح ریزی یک نقطه بر روی محور آبسیسا روی خود محور آبسیسا، یعنی محور قرار دارد. گاو نر، و بنابراین دارای یک ابسیسا برابر با آبسیسا خود نقطه است و ترتیب و کاربرد برآمدگی برابر با صفر است (از آنجایی که محورهای مختص و کاربردی در نقطه 0 ابسیسا را قطع می کنند). مختصات زیر را از برجستگی این نقاط بر روی محور آبسیسا بدست می آوریم:
آx (4; 0; 0);
بx (-3; 0; 0);
سیx(2;0;0).
5) برآمدگی یک نقطه بر روی محور ارتین بر روی خود محور ارتین، یعنی محور قرار دارد. اوه، و بنابراین دارای یک اردین برابر با خود نقطه است، و ابسیسا و اعمال برجستگی برابر با صفر است (از آنجایی که ابسیسا و محورهای کاربردی در نقطه 0 محور رده را قطع می کنند). مختصات زیر را از برجستگی این نقاط بر روی محور ارتین بدست می آوریم:
آy(0; 3; 0);
بy (0; 2; 0);
سیy(0;-3;0).
6) طرح ریزی یک نقطه بر روی محور کاربردی روی خود محور کاربردی، یعنی محور قرار دارد. اوز، و بنابراین دارای یک اطلاق برابر با کاربرد خود نقطه است، و ابسیسا و مختصات برجستگی برابر با صفر است (از آنجایی که محورهای ابسیسا و ارتین، محور اعمالی را در نقطه 0 قطع می کنند). مختصات زیر را از پیش بینی این نقاط بر روی محور کاربردی بدست می آوریم:
آz (0; 0; 5);
بz (0; 0; 1);
سیz(0; 0; 0).
مثال 9.در دستگاه مختصات دکارتی، نقاط در فضا داده می شوند
آ(2; 3; 1) ;
ب(5; -3; 2) ;
سی(-3; 2; -1) .
مختصات نقاط متقارن با این نقاط را با توجه به:
1) هواپیما اکسی ;
2) هواپیماها Oxz ;
3) هواپیما اویز ;
4) محورهای آبسیسا;
5) محورهای ترتیبی؛
6) محورها را اعمال کنید.
7) مبدا مختصات.
1) نقطه را در طرف دیگر محور "حرکت دهید". اکسی اکسی، دارای ابسیسا و مجملی برابر با ابسیسا و مختص یک نقطه معین و یک اطلاق مساوی از نظر بزرگی با انتزاعی یک نقطه داده شده، اما در مقابل علامت. بنابراین، مختصات زیر را از نقاط متقارن با داده های نسبت به صفحه بدست می آوریم اکسی :
آ"(2; 3; -1) ;
ب"(5; -3; -2) ;
ج"(-3; 2; 1) .
2) نقطه را در طرف دیگر محور "حرکت دهید". Oxzبه همان فاصله از شکلی که فضای مختصات را نشان می دهد، می بینیم که یک نقطه متقارن با یک نقطه داده شده نسبت به محور است. Oxz، دارای یک ابسیسا و اطلاق برابر با ابسیسا و اطلاق یک نقطه معین، و یک مجرای مساوی از نظر بزرگی با امتداد یک نقطه معین، اما در مقابل علامت. بنابراین، مختصات زیر را از نقاط متقارن با داده های نسبت به صفحه بدست می آوریم Oxz :
آ"(2; -3; 1) ;
ب"(5; 3; 2) ;
ج"(-3; -2; -1) .
3) "حرکت" نقطه در سمت دیگر محور اویزبه همان فاصله از شکلی که فضای مختصات را نشان می دهد، می بینیم که یک نقطه متقارن با یک نقطه داده شده نسبت به محور است. اویز، یک ترتیب و یک مصداق برابر با ترتیب و یک مضمون یک نقطه داده شده و یک ابسیسا از نظر مقدار با ابسیسا یک نقطه داده شده، اما در مقابل علامت خواهد داشت. بنابراین، مختصات زیر را از نقاط متقارن با داده های نسبت به صفحه بدست می آوریم اویز :
آ"(-2; 3; 1) ;
ب"(-5; -3; 2) ;
ج"(3; 2; -1) .
با قیاس با نقاط متقارن در یک صفحه و نقاطی در فضا که متقارن با داده های نسبت به صفحات هستند، توجه می کنیم که در مورد تقارن با توجه به برخی از محورهای دستگاه مختصات دکارتی در فضا، مختصات روی محور با توجه به که تقارن داده شده علامت خود را حفظ می کند و مختصات دو محور دیگر از نظر قدر مطلق با مختصات یک نقطه داده شده یکسان است، اما در علامت مخالف خواهد بود.
4) ابسیسا علامت خود را حفظ می کند، اما دستور و اعمال علامت ها را تغییر می دهند. بنابراین، مختصات زیر را از نقاط متقارن با داده ها نسبت به محور آبسیسا بدست می آوریم:
آ"(2; -3; -1) ;
ب"(5; 3; -2) ;
ج"(-3; -2; 1) .
5) منتخب علامت خود را حفظ می کند، اما انتزاع و اطلاق علامت ها را تغییر می دهند. بنابراین، مختصات زیر را از نقاط متقارن با داده ها نسبت به محور ارتین بدست می آوریم:
آ"(-2; 3; -1) ;
ب"(-5; -3; -2) ;
ج"(3; 2; 1) .
6) درخواست علامت خود را حفظ می کند، اما انتزاع و حکم تغییر علائم می دهد. بنابراین، مختصات زیر را از نقاط متقارن با داده ها نسبت به محور کاربردی بدست می آوریم:
آ"(-2; -3; 1) ;
ب"(-5; 3; 2) ;
ج"(3; -2; -1) .
7) بر اساس قیاس با تقارن در مورد نقاط روی صفحه، در مورد تقارن در مورد مبدأ مختصات، تمام مختصات یک نقطه متقارن با یک معین از نظر مقدار مطلق با مختصات یک نقطه معین برابر خواهد بود. اما در علامت مخالف بنابراین، مختصات زیر را از نقاط متقارن با داده ها نسبت به مبدا بدست می آوریم.
تعریف 1. محور اعداد ( خط شماره، خط مختصات) Ox خط مستقیمی است که نقطه O روی آن انتخاب می شود مبدا (منشا مختصات)(شکل 1)، جهت
O → ایکس
فهرست شده به عنوان جهت مثبتو یک قطعه مشخص می شود که طول آن در نظر گرفته می شود واحد طول.


تعریف 2. قطعه ای که طول آن به عنوان واحد طول در نظر گرفته شود مقیاس نامیده می شود.
هر نقطه در محور عدد دارای مختصاتی است که یک عدد واقعی است. مختصات نقطه O صفر است. مختصات یک نقطه دلخواه A که روی پرتو Ox قرار دارد با طول قطعه OA برابر است. مختصات یک نقطه دلخواه A از محور عددی که روی پرتو Ox قرار ندارد منفی است و در مقدار مطلق برابر با طول قطعه OA است.
تعریف 3. سیستم مختصات دکارتی مستطیلی Oxy در هواپیمابا دو نفر تماس بگیرید عمود برمحورهای عددی Ox و Oy با همان مقیاسو نقطه مرجع مشترکدر نقطه O، و به گونه ای که چرخش از پرتو Ox با زاویه 90 درجه به پرتو Oy در جهت انجام شود. پادساعتگرد(شکل 2).


توجه داشته باشید. سیستم مختصات دکارتی مستطیلی Oxy که در شکل 2 نشان داده شده است نامیده می شود سیستم مختصات درست، بر خلاف سیستم مختصات چپ، که در آن چرخش تیر Ox با زاویه 90 درجه نسبت به تیر Oy در جهت عقربه های ساعت انجام می شود. در این راهنما ما ما فقط سیستم های مختصات راست دست را در نظر می گیریم، بدون اینکه مشخص شود.
اگر سیستمی از مختصات دکارتی مستطیلی Oxy را در صفحه معرفی کنیم، آنگاه هر نقطه از صفحه به دست خواهد آمد. دو مختصات – اوکیساو ترتیب، که به صورت زیر محاسبه می شوند. بگذارید A یک نقطه دلخواه در هواپیما باشد. بگذارید عمودها را از نقطه A رها کنیم A.A. 1 و A.A. 2 تا خطوط مستقیم Ox و Oy به ترتیب (شکل 3).


تعریف 4. آبسیسا نقطه A مختصات نقطه است آ 1 در محور عددی Ox، مختصات نقطه A مختصات نقطه است آ 2 در محور اعداد Oy.
تعیین مختصات (ابسیسا و مختصات) نقطه A در سیستم مختصات دکارتی مستطیلی Oxy (شکل 4) معمولا نشان داده می شود آ(ایکس;y) یا آ = (ایکس; y).
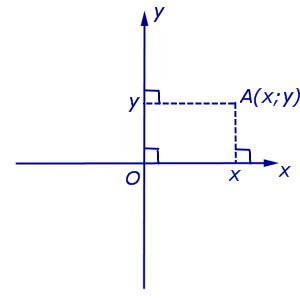

توجه داشته باشید. نقطه O، نامیده می شود اصل و نسب، مختصات دارد O(0 ; 0) .
تعریف 5. در سیستم مختصات دکارتی مستطیلی Oxy، محور عددی Ox را محور آبسیسا و محور عددی Oy را محور ارتین می نامند (شکل 5).
تعریف 6. هر سیستم مختصات دکارتی مستطیلی، صفحه را به 4 ربع (ربع) تقسیم می کند که شماره گذاری آنها در شکل 5 نشان داده شده است.


تعریف 7. صفحه ای که بر روی آن سیستم مختصات دکارتی مستطیلی داده می شود نامیده می شود هواپیمای مختصات.
توجه داشته باشید. محور آبسیسا در صفحه مختصات با معادله مشخص می شود y= 0، محور ارتین در صفحه مختصات با معادله داده می شود ایکس = 0.
بیانیه 1. فاصله بین دو نقطههواپیمای مختصات
آ 1 (ایکس 1 ;y 1) و آ 2 (ایکس 2 ;y 2)
محاسبه شد طبق فرمول
اثبات شکل 6 را در نظر بگیرید.


| |آ 1 آ 2 | 2 = = (ایکس 2 -ایکس 1) 2 + (y 2 -y 1) 2 . | (1) |
از این رو،
Q.E.D.
معادله دایره در صفحه مختصات
اجازه دهید در صفحه مختصات Oxy (شکل 7) دایره ای به شعاع R با مرکز در نقطه در نظر بگیریم. آ 0 (ایکس 0 ;y 0) .











