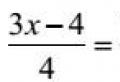Sode in lihe funkcije. Kako določiti sode in lihe funkcije Enačbe, ki dajejo grafe sodih funkcij

- ; soda funkcija se pokliče, ko je za kateri koli dve različni vrednosti njenega argumenta f (x) =f(x) , na primer y= |x|; liho - taka funkcija, ko je f (x) \u003d - f (x), na primer y \u003d x2n + 1, kjer je n ... ... Ekonomsko-matematični slovar

sode in lihe funkcije- Sodo funkcijo pokličemo, ko je za kateri koli dve različni vrednosti njenega argumenta f (x) =f(x) , na primer y= |x|; taka funkcija je liha, če je f(x) = f(x), na primer y= x2n+1, kjer je n poljubno naravno število. Funkcije, ki niso niti... Priročnik tehničnega prevajalca

PARITETA- kvantno število, ki označuje simetrijo valovne funkcije fizikalnega sistema ali elementarnega delca pri nekaterih diskretnih transformacijah: če pri taki transformaciji? ne spremeni predznaka, potem je pariteta pozitivna, če se spremeni, potem pariteta ... ... Veliki enciklopedični slovar

PARITETA RAVNI- pariteta stanja fizičnega. sistem (valovna pariteta. funkcije), ki ustreza danemu nivoju energije. Takšna karakterizacija nivojev je mogoča za sistem h c, med katerima je el. magn. ali strup. sile, ki ohranjajo pariteto. Ob upoštevanju šibke interakcije ... ... Fizična enciklopedija

Pariteta

Pariteta (matematika)- Pariteta v teoriji števil je zmožnost celega števila, da se brez ostanka deli z 2. Pariteta funkcije v matematični analizi določa, ali funkcija spremeni predznak, ko se spremeni predznak argumenta: za sodo / liho funkcijo. Pariteta v kvantni mehaniki ... ... Wikipedia

TRIGONOMETRIČNE FUNKCIJE- razred elementarnih funkcij: sinus, kosinus, tangens, kotangens, sekans, kosekans. Ustrezno označeno: sin x, cos x, tg x, ctg x, sec x, cosec x. Trigonometrične funkcije realnega argumenta. Naj bo A točka kroga s središčem v ... ... Matematična enciklopedija

NOTRANJA PARITETA- (P), ena od značilnosti (kvantnih števil) elementov. tsy, ki določa obnašanje njegove valovne funkcije y med prostorsko inverzijo (zrcalni odboj), to je, ko se spremenijo koordinate x® x, y® y, z® z. Če s takim odsevom y ne spremeni predznaka, V. h. h tsy ... ... Fizična enciklopedija

Pariteta naboja- Konjugacija naboja je operacija zamenjave delca z antidelcem (na primer elektrona s pozitronom). Pariteta naboja Pariteta naboja je kvantno število, ki določa obnašanje valovne funkcije delca med operacijo zamenjave delca z antidelcem ... ... Wikipedia

Ciklično preverjanje parnosti- Algoritem za izračun kontrolne vsote (angl. Cyclic redundancy code, CRC cyclic redundancy code) je metoda digitalne identifikacije določenega zaporedja podatkov, ki je sestavljena iz izračuna kontrolne vrednosti njegovega cikličnega ... ... Wikipedia

Nazaj naprej

Pozor! Predogled diapozitiva je zgolj informativne narave in morda ne predstavlja celotnega obsega predstavitve. Če vas to delo zanima, prenesite polno različico.

Cilji:

• oblikovati koncept parnih in lihih funkcij, učiti sposobnost določanja in uporabe teh lastnosti pri preučevanju funkcij, risanju;
• razvijati ustvarjalno dejavnost učencev, logično razmišljanje, sposobnost primerjave, posploševanja;
• gojiti marljivost, matematično kulturo; razvijati komunikacijske sposobnosti .

Oprema: multimedijska instalacija, interaktivna tabla, izročki.

Oblike dela: frontalni in skupinski z elementi iskalne in raziskovalne dejavnosti.

Viri informacij:

1. Algebra razred 9 A.G. Mordkovich. Učbenik.
2. Algebra 9. razred A.G. Mordkovich. Opravilna knjiga.
3. Algebra 9. razred. Naloge za učenje in razvoj učencev. Belenkova E.Yu. Lebedintseva E.A.

MED POUKOM

1. Organizacijski trenutek

Določitev ciljev in ciljev lekcije.

2. Preverjanje domače naloge

10.17 (Problem knjiga 9. razred A.G. Mordkovich).

A) pri = f(X), f(X) =

b) f (–2) = –3; f (0) = –1; f(5) = 69;

c) 1. D( f) = [– 2; + ∞)
2. E( f) = [– 3; + ∞)
3. f(X) = 0 za X ~ 0,4
4. f(X) >0 pri X > 0,4 ; f(X) < 0 при – 2 < X < 0,4.
5. Funkcija se poveča z X € [– 2; + ∞)
6. Funkcija je omejena od spodaj.
7. pri najem = - 3, pri naib ne obstaja
8. Funkcija je neprekinjena.

(Ali ste uporabili algoritem za raziskovanje funkcij?) Zdrs.

2. Poglejmo tabelo, ki ste jo vprašali na prosojnici.

Izpolni tabelo
	Domena	Funkcijske ničle	Intervali konstantnosti		Koordinate presečišč grafa z Oy
		x = -5, x = 2	х € (–5;3) U U(2;∞)	х € (–∞;–5) U U (–3;2)
	x ∞ -5, x ≠ 2		х € (–5;3) U U(2;∞)	х € (–∞;–5) U U (–3;2)
	x ≠ -5, x ≠ 2		x € (–∞; –5) U U(2;∞)	x € (–5; 2)

3. Posodobitev znanja

– Funkcije so podane.
– Določite domeno definicije za vsako funkcijo.
– Primerjaj vrednost posamezne funkcije za vsak par vrednosti argumentov: 1 in – 1; 2 in - 2.
– Za katero od danih funkcij v domeni definicije veljajo enakosti f(– X) = f(X), f(– X) = – f(X)? (vnesite podatke v tabelo) Zdrs

		f(1) in f(– 1)	f(2) in f(– 2)	lestvice	f(– X) = –f(X)	f(– X) = f(X)
1. f(X) =
2. f(X) = X 3
3. f(X) = | X |
4.f(X) = 2X – 3
5. f(X) =	X ≠ 0
6. f(X)=	X > –1		in ni definiran.

4. Novo gradivo

- Med opravljanjem tega dela, fantje, smo razkrili še eno lastnost funkcije, ki vam ni znana, a nič manj pomembna od drugih - to je parnost in lihost funkcije. Zapišite temo lekcije: "Sode in lihe funkcije", naša naloga je, da se naučimo določiti sode in lihe funkcije, ugotoviti pomen te lastnosti pri študiju funkcij in risanju.
Torej, poiščimo definicije v učbeniku in preberimo (str. 110) . Zdrs

Def. 1 funkcija pri = f (X), definirana na množici X, se imenuje celo, če za kakršno koli vrednost XЄ X v teku enakost f (–x) = f (x). Navedite primere.

Def. 2 funkcija y = f(x), definirana na množici X se imenuje Čuden, če za kakršno koli vrednost XЄ X izpolnjena je enakost f(–х)= –f(х). Navedite primere.

Kje smo srečali izraza "sodo" in "liho"?
Katera od teh funkcij bo enakomerna, kaj mislite? Zakaj? Kateri so nenavadni? Zakaj?
Za katero koli funkcijo obrazca pri= x n, Kje n je celo število, lahko trdimo, da je funkcija liha za n je liho in funkcija je soda za n- celo.
– Ogled funkcij pri= in pri = 2X– 3 ni ne sodo ne liho, saj enakosti niso izpolnjene f(– X) = – f(X), f(– X) = f(X)

Preučevanje vprašanja, ali je funkcija soda ali liha, se imenuje preučevanje funkcije za pariteto. Zdrs

Definiciji 1 in 2 sta obravnavali vrednosti funkcije pri x in - x, zato se predpostavlja, da je funkcija definirana tudi pri vrednosti X in pri - X.

uradna razvojna pomoč 3.Če številska množica skupaj z vsakim svojim elementom x vsebuje nasprotni element x, potem množica X imenujemo simetrična množica.

Primeri:

(–2;2), [–5;5]; (∞;∞) so simetrične množice in , [–5;4] so nesimetrične.

- Ali imajo sode funkcije domeno definicije - simetrično množico? Tiste nenavadne?
- Če D( f) je asimetrična množica, kaj je potem funkcija?
– Tako, če funkcija pri = f(X) sodo ali liho, potem je njegova definicijska domena D( f) je simetrična množica. Toda ali velja obratno, če je domena funkcije simetrična množica, potem je soda ali liha?
- Prisotnost simetrične množice domene definicije je torej nujen pogoj, ne pa tudi zadosten.
– Kako lahko torej raziščemo funkcijo za pariteto? Poskusimo napisati algoritem.

Zdrs

Algoritem za preverjanje paritete funkcije

1. Ugotovite, ali je domena funkcije simetrična. Če ne, potem funkcija ni niti soda niti liha. Če da, pojdite na 2. korak algoritma.

2. Napišite izraz za f(–X).

3. Primerjaj f(–X).In f(X):

• če f(–X).= f(X), potem je funkcija soda;
• če f(–X).= – f(X), potem je funkcija liha;
• če f(–X) ≠ f(X) In f(–X) ≠ –f(X), potem funkcija ni niti soda niti liha.

Primeri:

Raziščite funkcijo za pariteto a) pri= x 5 +; b) pri= ; V) pri= .

rešitev.

a) h (x) \u003d x 5 +,

1) D(h) = (–∞; 0) U (0; +∞), simetrična množica.

2) h (- x) \u003d (-x) 5 + - x5 - \u003d - (x 5 +),

3) h (- x) \u003d - h (x) \u003d\u003e funkcija h(x)= x 5 + liho.

b) y =,

pri = f(X), D(f) = (–∞; –9)? (–9; +∞), asimetrična množica, zato funkcija ni niti soda niti liha.

V) f(X) = , y = f(x),

1) D( f) = (–∞; 3] ≠ ; b) (∞; –2), (–4; 4]?

Možnost 2

1. Ali je dana množica simetrična: a) [–2;2]; b) (∞; 0], (0; 7) ?

A); b) y \u003d x (5 - x 2). 2. Preglejte funkcijo za pariteto:

a) y \u003d x 2 (2x - x 3), b) y \u003d

3. Na sl. narisano pri = f(X), za vse X, ki izpolnjuje pogoj X? 0.
Narišite funkcijo pri = f(X), če pri = f(X) je soda funkcija.

3. Na sl. narisano pri = f(X), za vse x, ki ustrezajo x? 0.
Narišite funkcijo pri = f(X), če pri = f(X) je liha funkcija.

Medsebojno preverjanje vključeno zdrs.

6. Domača naloga: №11.11, 11.21,11.22;

Dokaz geometrijskega pomena paritetne lastnosti.

*** (Dodelitev možnosti USE).

1. Liha funkcija y \u003d f (x) je definirana na celotni realni črti. Za vsako nenegativno vrednost spremenljivke x vrednost te funkcije sovpada z vrednostjo funkcije g( X) = X(X + 1)(X + 3)(X– 7). Poiščite vrednost funkcije h( X) = pri X = 3.

7. Povzemanje

Odvisnost spremenljivke y od spremenljivke x, pri kateri vsaka vrednost x ustreza eni sami vrednosti y, se imenuje funkcija. Zapis je y=f(x). Vsaka funkcija ima številne osnovne lastnosti, kot so monotonost, parnost, periodičnost in druge.

Razmislite o lastnosti paritete podrobneje.

Funkcija y=f(x) je poklicana, tudi če izpolnjuje naslednja dva pogoja:

2. Vrednost funkcije v točki x, ki pripada obsegu funkcije, mora biti enaka vrednosti funkcije v točki -x. To pomeni, da mora za katero koli točko x iz domene funkcije veljati naslednja enakost f (x) \u003d f (-x).

Graf sode funkcije

Če zgradite graf sode funkcije, bo ta simetričen glede na os y.

Na primer, funkcija y=x^2 je soda. Preverimo. Definicijsko področje je celotna numerična os, kar pomeni, da je simetrična glede na točko O.

Vzemite poljuben x=3. f(x)=3^2=9.

f(-x)=(-3)^2=9. Zato je f(x) = f(-x). Tako sta za nas izpolnjena oba pogoja, kar pomeni, da je funkcija soda. Spodaj je graf funkcije y=x^2.

Slika prikazuje, da je graf simetričen glede na os y.

Graf lihe funkcije

Funkcija y=f(x) se imenuje liha, če izpolnjuje naslednja dva pogoja:

1. Domena dane funkcije mora biti simetrična glede na točko O. To pomeni, da če neka točka a pripada domeni funkcije, mora tudi ustrezna točka -a pripadati domeni dane funkcije.

2. Za katero koli točko x iz domene funkcije mora biti izpolnjena naslednja enakost f (x) \u003d -f (x).

Graf lihe funkcije je simetričen glede na točko O - izhodišče. Na primer, funkcija y=x^3 je liha. Preverimo. Definicijsko področje je celotna numerična os, kar pomeni, da je simetrična glede na točko O.

Vzemimo poljuben x=2. f(x)=2^3=8.

f(-x)=(-2)^3=-8. Zato je f(x) = -f(x). Tako sta za nas izpolnjena oba pogoja, kar pomeni, da je funkcija liha. Spodaj je graf funkcije y=x^3.

Slika jasno kaže, da je liha funkcija y=x^3 simetrična glede na izvor.

Skrij Pokaži

Načini za nastavitev funkcije

Naj bo funkcija podana s formulo: y=2x^(2)-3 . Če neodvisni spremenljivki x dodelite poljubno vrednost, lahko uporabite to formulo za izračun ustreznih vrednosti odvisne spremenljivke y. Na primer, če x=-0,5 , potem z uporabo formule dobimo, da je ustrezna vrednost y y=2 \cdot (-0,5)^(2)-3=-2,5 .

Glede na katero koli vrednost, ki jo prevzame argument x v formuli y=2x^(2)-3, je mogoče izračunati samo eno vrednost funkcije, ki ji ustreza. Funkcijo lahko predstavimo kot tabelo:

x	−2	−1	0	1	2	3
l	−4	−3	−2	−1	0	1

S to tabelo lahko ugotovite, da bo za vrednost argumenta -1 ustrezala vrednost funkcije -3; in vrednost x=2 bo ustrezala y=0 itd. Pomembno je tudi vedeti, da vsaka vrednost argumenta v tabeli ustreza le eni vrednosti funkcije.

Več funkcij je mogoče nastaviti z uporabo grafov. S pomočjo grafa ugotovimo, katera vrednost funkcije korelira z določeno vrednostjo x. Najpogosteje bo to približna vrednost funkcije.

Soda in liha funkcija

Funkcija je celo funkcijo, ko je f(-x)=f(x) za kateri koli x iz domene. Takšna funkcija bo simetrična glede na os Oy.

Funkcija je nenavadna funkcija ko je f(-x)=-f(x) za kateri koli x v domeni. Takšna funkcija bo simetrična glede na izvor O (0;0) .

Funkcija je niti približno, niti čudno in poklical splošna funkcija kadar nima simetrije glede na os ali izhodišče.

Za pariteto preučimo naslednjo funkcijo:

f(x)=3x^(3)-7x^(7)

D(f)=(-\infty ; +\infty) s simetrično domeno definicije glede izvora. f(-x)= 3 \cdot (-x)^(3)-7 \cdot (-x)^(7)= -3x^(3)+7x^(7)= -(3x^(3)-7x^(7))= -f(x).

Zato je funkcija f(x)=3x^(3)-7x^(7) liha.

Periodična funkcija

Funkcija y=f(x) , v domeni katere f(x+T)=f(x-T)=f(x) velja za vsak x, se imenuje periodična funkcija z obdobjem T \neq 0 .

Ponovitev grafa funkcije na poljubnem segmentu abscisne osi, ki ima dolžino T .

Intervali, kjer je funkcija pozitivna, to je f (x) > 0 - segmenti abscisne osi, ki ustrezajo točkam grafa funkcije, ki ležijo nad abscisno osjo.

f(x) > 0 vklopljeno (x_(1); x_(2)) \skodelica (x_(3); +\infty)

Intervali, kjer je funkcija negativna, tj. f(x)< 0 - отрезки оси абсцисс, которые отвечают точкам графика функции, лежащих ниже оси абсцисс.

f(x)< 0 на (-\infty; x_(1)) \skodelica (x_(2); x_(3))

Omejitev delovanja

omejena od spodaj običajno je poklicati funkcijo y=f(x), x \in X, ko obstaja število A, za katerega velja neenakost f(x) \geq A za katerikoli x \in X .

Primer spodaj omejene funkcije: y=\sqrt(1+x^(2)), ker je y=\sqrt(1+x^(2)) \geq 1 za poljuben x .

omejena od zgoraj funkcija y=f(x), x \in X se pokliče, če obstaja število B, za katero velja neenakost f(x) \neq B za vsak x \in X .

Spodaj omejen primer funkcije: y=\sqrt(1-x^(2)), x \in [-1;1] ker je y=\sqrt(1+x^(2)) \neq 1 za kateri koli x \in [-1;1] .

Omejeno je običajno poklicati funkcijo y=f(x), x \in X, ko obstaja število K > 0, za katero velja neenakost \left | f(x) \desno | \neq K za poljuben x \in X .

Primer omejene funkcije: y=\sin x je omejena na celo številsko premico, ker \levo | \sin x \desno | \neq 1.

Naraščajoča in padajoča funkcija

Običajno govorimo o funkciji, ki narašča na obravnavanem intervalu kot povečanje funkcije ko bo večja vrednost x ustrezala večji vrednosti funkcije y=f(x) . Od tu se izkaže, da če iz obravnavanega intervala vzamemo dve poljubni vrednosti argumenta x_(1) in x_(2) ter x_(1) > x_(2) , bo y(x_(1)) > y(x_(2)) .

Imenuje se funkcija, ki pada na obravnavanem intervalu zmanjševanje funkcije ko bo večja vrednost x ustrezala manjši vrednosti funkcije y(x) . Od tu se izkaže, da če iz obravnavanega intervala vzamemo dve poljubni vrednosti argumenta x_(1) in x_(2) ter x_(1) > x_(2) , bo y(x_(1))< y(x_{2}) .

Funkcijske korenine običajno je poimenovati točke, v katerih funkcija F=y(x) seka abscisno os (dobimo jih kot rezultat reševanja enačbe y(x)=0 ).

a) Če soda funkcija narašča za x > 0, potem pada za x< 0

b) Ko soda funkcija pada za x > 0, potem narašča za x< 0

c) Ko liha funkcija narašča za x > 0, potem narašča tudi za x< 0

d) Ko liha funkcija pada za x > 0, potem se zmanjšuje tudi za x< 0

Ekstremne funkcije

Minimalna točka funkcije y=f(x) običajno imenujemo takšno točko x=x_(0) , v kateri bo njena okolica imela druge točke (razen točke x=x_(0) ), zanje pa velja neenakost f( x) > f (x_(0)) . y_(min) - oznaka funkcije v točki min.

Najvišja točka funkcije y=f(x) običajno imenujemo takšno točko x=x_(0) , v kateri bo njena soseska imela druge točke (razen točke x=x_(0) ), nato pa neenakost f(x) bo zanje zadovoljen< f(x^{0}) . y_{max} - обозначение функции в точке max.

Nujen pogoj

Po Fermatovem izreku: f"(x)=0, potem ko je funkcija f(x) , ki je diferenciabilna v točki x_(0) , se bo v tej točki pojavil ekstrem.

Zadosten pogoj

1. Ko se predznak odvoda spremeni iz plusa v minus, bo x_(0) najmanjša točka;
2. x_(0) - bo največja točka le, ko odvod spremeni predznak iz minusa v plus, ko gre skozi stacionarno točko x_(0) .

Največja in najmanjša vrednost funkcije na intervalu

Koraki izračuna:

1. Iskanje izpeljanke f"(x) ;
2. Poiščemo stacionarne in kritične točke funkcije ter izberemo tiste, ki pripadajo intervalu;
3. Vrednosti funkcije f(x) najdemo na stacionarnih in kritičnih točkah ter koncih segmenta. Najmanjši rezultat bo najmanjša vrednost funkcije, in več - največji.

. Če želite to narediti, uporabite grafični papir ali grafični kalkulator. Izberite poljubno število številskih vrednosti za neodvisno spremenljivko x (\displaystyle x) in jih vključite v funkcijo za izračun vrednosti odvisne spremenljivke y (\displaystyle y). Najdene koordinate točk postavite na koordinatno ravnino in nato povežite te točke, da zgradite graf funkcije.

• V funkcijo nadomestite pozitivne številske vrednosti x (\displaystyle x) in ustrezne negativne številske vrednosti. Na primer, glede na funkcijo f (x) = 2 x 2 + 1 (\displaystyle f(x)=2x^(2)+1). Vanjo nadomestite naslednje vrednosti x (\displaystyle x):

Preverite, ali je graf funkcije simetričen glede na os y. Simetrija se nanaša na zrcalno sliko grafa glede na os y. Če se del grafa desno od osi y (pozitivne vrednosti neodvisne spremenljivke) ujema z delom grafa levo od osi y (negativne vrednosti neodvisne spremenljivke), graf je simetričen glede na os y. Če je funkcija simetrična glede na os y, je funkcija soda.

Preverite, ali je graf funkcije simetričen glede na izvor. Izhodišče je točka s koordinatami (0,0). Simetrija glede na izvor pomeni pozitivno vrednost y (\displaystyle y)(s pozitivno vrednostjo x (\displaystyle x)) ustreza negativni vrednosti y (\displaystyle y)(z negativno vrednostjo x (\displaystyle x)), in obratno. Lihe funkcije imajo simetrijo glede na izvor.

Preverite, ali ima graf funkcije simetrijo. Zadnja vrsta funkcije je funkcija, katere graf nima simetrije, to pomeni, da ni zrcalne slike glede na os y in glede na izvor. Na primer, glede na funkcijo.

• V funkcijo nadomestite več pozitivnih in ustreznih negativnih vrednosti x (\displaystyle x):
• Glede na dobljene rezultate simetrije ni. Vrednote y (\displaystyle y) za nasprotne vrednosti x (\displaystyle x) se ne ujemajo in niso nasprotne. Tako funkcija ni niti soda niti liha.
• Upoštevajte, da funkcija f (x) = x 2 + 2 x + 1 (\displaystyle f(x)=x^(2)+2x+1) lahko zapišemo takole: f (x) = (x + 1) 2 (\displaystyle f(x)=(x+1)^(2)). Zapisana v tej obliki se zdi, da je funkcija soda, ker obstaja sodi eksponent. Toda ta primer dokazuje, da oblike funkcije ni mogoče hitro določiti, če je neodvisna spremenljivka v oklepaju. V tem primeru morate odpreti oklepaje in analizirati nastale eksponente.