Свойства сферы и шара. Шар и сфера, объем шара, площадь сферы, формулы. Секущая, хорда, секущая плоскость сферы и их свойства

В пятом веке до нашей эры древнегреческий философ Зенон Элейский сформулировал свои знаменитые апории, самой известной из которых является апория "Ахиллес и черепаха". Вот как она звучит:

Допустим, Ахиллес бежит в десять раз быстрее, чем черепаха, и находится позади неё на расстоянии в тысячу шагов. За то время, за которое Ахиллес пробежит это расстояние, черепаха в ту же сторону проползёт сто шагов. Когда Ахиллес пробежит сто шагов, черепаха проползёт ещё десять шагов, и так далее. Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху.

Это рассуждение стало логическим шоком для всех последующих поколений. Аристотель, Диоген, Кант, Гегель, Гильберт... Все они так или иначе рассматривали апории Зенона. Шок оказался настолько сильным, что "... дискуссии продолжаются и в настоящее время, прийти к общему мнению о сущности парадоксов научному сообществу пока не удалось... к исследованию вопроса привлекались математический анализ, теория множеств, новые физические и философские подходы; ни один из них не стал общепризнанным решением вопроса... " [Википедия, " Апории Зенона "]. Все понимают, что их дурят, но никто не понимает, в чем заключается обман.

С точки зрения математики, Зенон в своей апории наглядно продемонстрировал переход от величины к . Этот переход подразумевает применение вместо постоянных. Насколько я понимаю, математический аппарат применения переменных единиц измерения либо ещё не разработан, либо его не применяли к апории Зенона. Применение же нашей обычной логики приводит нас в ловушку. Мы, по инерции мышления, применяем постоянные единицы измерения времени к обратной величине. С физической точки зрения это выглядит, как замедление времени до его полной остановки в момент, когда Ахиллес поравняется с черепахой. Если время останавливается, Ахиллес уже не может перегнать черепаху.

Если перевернуть привычную нам логику, всё становится на свои места. Ахиллес бежит с постоянной скоростью. Каждый последующий отрезок его пути в десять раз короче предыдущего. Соответственно, и время, затрачиваемое на его преодоление, в десять раз меньше предыдущего. Если применять понятие "бесконечность" в этой ситуации, то правильно будет говорить "Ахиллес бесконечно быстро догонит черепаху".

Как избежать этой логической ловушки? Оставаться в постоянных единицах измерения времени и не переходить к обратным величинам. На языке Зенона это выглядит так:

За то время, за которое Ахиллес пробежит тысячу шагов, черепаха в ту же сторону проползёт сто шагов. За следующий интервал времени, равный первому, Ахиллес пробежит ещё тысячу шагов, а черепаха проползет сто шагов. Теперь Ахиллес на восемьсот шагов опережает черепаху.

Этот подход адекватно описывает реальность без всяких логических парадоксов. Но это не полное решение проблемы. На Зеноновскую апорию "Ахиллес и черепаха" очень похоже утверждение Эйнштейна о непреодолимости скорости света. Эту проблему нам ещё предстоит изучить, переосмыслить и решить. И решение нужно искать не в бесконечно больших числах, а в единицах измерения.

Другая интересная апория Зенона повествует о летящей стреле:

Летящая стрела неподвижна, так как в каждый момент времени она покоится, а поскольку она покоится в каждый момент времени, то она покоится всегда.

В этой апории логический парадокс преодолевается очень просто - достаточно уточнить, что в каждый момент времени летящая стрела покоится в разных точках пространства, что, собственно, и является движением. Здесь нужно отметить другой момент. По одной фотографии автомобиля на дороге невозможно определить ни факт его движения, ни расстояние до него. Для определения факта движения автомобиля нужны две фотографии, сделанные из одной точки в разные моменты времени, но по ним нельзя определить расстояние. Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в один момент времени, но по ним нельзя определить факт движения (естественно, ещё нужны дополнительные данные для расчетов, тригонометрия вам в помощь). На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве - это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования.

среда, 4 июля 2018 г.

Очень хорошо различия между множеством и мультимножеством описаны в Википедии . Смотрим.

Как видите, "во множестве не может быть двух идентичных элементов", но если идентичные элементы во множестве есть, такое множество называется "мультимножество". Подобную логику абсурда разумным существам не понять никогда. Это уровень говорящих попугаев и дрессированных обезьян, у которых разум отсутствует от слова "совсем". Математики выступают в роли обычных дрессировщиков, проповедуя нам свои абсурдные идеи.

Когда-то инженеры, построившие мост, во время испытаний моста находились в лодке под мостом. Если мост обрушивался, бездарный инженер погибал под обломками своего творения. Если мост выдерживал нагрузку, талантливый инженер строил другие мосты.

Как бы математики не прятались за фразой "чур, я в домике", точнее "математика изучает абстрактные понятия", есть одна пуповина, которая неразрывно связывает их с реальностью. Этой пуповиной являются деньги. Применим математическую теорию множеств к самим математикам.

Мы очень хорошо учили математику и сейчас сидим в кассе, выдаем зарплату. Вот приходит к нам математик за своими деньгами. Отсчитываем ему всю сумму и раскладываем у себя на столе на разные стопки, в которые складываем купюры одного достоинства. Затем берем с каждой стопки по одной купюре и вручаем математику его "математическое множество зарплаты". Поясняем математику, что остальные купюры он получит только тогда, когда докажет, что множество без одинаковых элементов не равно множеству с одинаковыми элементами. Вот здесь начнется самое интересное.

В первую очередь, сработает логика депутатов: "к другим это применять можно, ко мне - низьзя!". Дальше начнутся уверения нас в том, что на купюрах одинакового достоинства имеются разные номера купюр, а значит их нельзя считать одинаковыми элементами. Хорошо, отсчитываем зарплату монетами - на монетах нет номеров. Здесь математик начнет судорожно вспоминать физику: на разных монетах имеется разное количество грязи, кристаллическая структура и расположение атомов у каждой монеты уникально...

А теперь у меня самый интересный вопрос: где проходит та грань, за которой элементы мультимножества превращаются в элементы множества и наоборот? Такой грани не существует - всё решают шаманы, наука здесь и близко не валялась.

Вот смотрите. Мы отбираем футбольные стадионы с одинаковой площадью поля. Площадь полей одинакова - значит у нас получилось мультимножество. Но если рассматривать названия этих же стадионов - у нас получается множество, ведь названия разные. Как видите, один и тот же набор элементов одновременно является и множеством, и мультимножеством. Как правильно? А вот здесь математик-шаман-шуллер достает из рукава козырный туз и начинает нам рассказывать либо о множестве, либо о мультимножестве. В любом случае он убедит нас в своей правоте.

Чтобы понять, как современные шаманы оперируют теорией множеств, привязывая её к реальности, достаточно ответить на один вопрос: чем элементы одного множества отличаются от элементов другого множества? Я вам покажу, без всяких "мыслимое как не единое целое" или "не мыслимое как единое целое".

воскресенье, 18 марта 2018 г.

Сумма цифр числа - это пляска шаманов с бубном, которая к математике никакого отношения не имеет. Да, на уроках математики нас учат находить сумму цифр числа и пользоваться нею, но на то они и шаманы, чтобы обучать потомков своим навыкам и премудростям, иначе шаманы просто вымрут.

Вам нужны доказательства? Откройте Википедию и попробуйте найти страницу "Сумма цифр числа". Её не существует. Нет в математике формулы, по которой можно найти сумму цифр любого числа. Ведь цифры - это графические символы, при помощи которых мы записываем числа и на языке математики задача звучит так: "Найти сумму графических символов, изображающих любое число". Математики эту задачу решить не могут, а вот шаманы - элементарно.

Давайте разберемся, что и как мы делаем для того, чтобы найти сумму цифр заданного числа. И так, пусть у нас есть число 12345. Что нужно сделать для того, чтобы найти сумму цифр этого числа? Рассмотрим все шаги по порядку.

1. Записываем число на бумажке. Что же мы сделали? Мы преобразовали число в графический символ числа. Это не математическое действие.

2. Разрезаем одну полученную картинку на несколько картинок, содержащих отдельные цифры. Разрезание картинки - это не математическое действие.

3. Преобразовываем отдельные графические символы в числа. Это не математическое действие.

4. Складываем полученные числа. Вот это уже математика.

Сумма цифр числа 12345 равна 15. Вот такие вот "курсы кройки и шитья" от шаманов применяют математики. Но это ещё не всё.

С точки зрения математики не имеет значения, в какой системе счисления мы записываем число. Так вот, в разных системах счисления сумма цифр одного и того же числа будет разной. В математике система счисления указывается в виде нижнего индекса справа от числа. С большим числом 12345 я не хочу голову морочить, рассмотрим число 26 из статьи про . Запишем это число в двоичной, восьмеричной, десятичной и шестнадцатеричной системах счисления. Мы не будем рассматривать каждый шаг под микроскопом, это мы уже сделали. Посмотрим на результат.

Как видите, в разных системах счисления сумма цифр одного и того же числа получается разной. Подобный результат к математике никакого отношения не имеет. Это всё равно, что при определении площади прямоугольника в метрах и сантиметрах вы получали бы совершенно разные результаты.

Ноль во всех системах счисления выглядит одинаково и суммы цифр не имеет. Это ещё один аргумент в пользу того, что . Вопрос к математикам: как в математике обозначается то, что не является числом? Что, для математиков ничего, кроме чисел, не существует? Для шаманов я могу такое допустить, но для ученых - нет. Реальность состоит не только из чисел.

Полученный результат следует рассматривать как доказательство того, что системы счисления являются единицами измерения чисел. Ведь мы не можем сравнивать числа с разными единицами измерения. Если одни и те же действия с разными единицами измерения одной и той же величины приводят к разным результатам после их сравнения, значит это не имеет ничего общего с математикой.

Что же такое настоящая математика? Это когда результат математического действия не зависит от величины числа, применяемой единицы измерения и от того, кто это действие выполняет.

Табличка на двери Открывает дверь и говорит:

Ой! А это разве не женский туалет?
- Девушка! Это лаборатория по изучению индефильной святости душ при вознесении на небеса! Нимб сверху и стрелочка вверх. Какой еще туалет?

Женский... Нимб сверху и стрелочка вниз - это мужской.

Если у вас перед глазами несколько раз в день мелькает вот такое вот произведение дизайнерского искусства,

Тогда не удивительно, что в своем автомобиле вы вдруг обнаруживаете странный значок:

Лично я делаю над собой усилие, чтобы в какающем человеке (одна картинка), увидеть минус четыре градуса (композиция из нескольких картинок: знак минус, цифра четыре, обозначение градусов). И я не считаю эту девушку дурой, не знающей физику. Просто у неё дугой стереотип восприятия графических образов. И математики нас этому постоянно учат. Вот пример.

1А - это не "минус четыре градуса" или "один а". Это "какающий человек" или число "двадцать шесть" в шестнадцатеричной системе счисления. Те люди, которые постоянно работают в этой системе счисления, автоматически воспринимают цифру и букву как один графический символ.

Умножение и деление дробей.

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно "не очень..."
И для тех, кто "очень даже...")

Эта операция гораздо приятнее сложения-вычитания ! Потому что проще. Напоминаю: чтобы умножить дробь на дробь, нужно перемножить числители (это будет числитель результата) и знаменатели (это будет знаменатель). То есть:

Например:

Всё предельно просто . И, пожалуйста, не ищите общий знаменатель! Не надо его здесь…

Чтобы разделить дробь на дробь, нужно перевернуть вторую (это важно!) дробь и их перемножить, т.е.:

Например:

Если попалось умножение или деление с целыми числами и дробями - ничего страшного. Как и при сложении, делаем из целого числа дробь с единицей в знаменателе - и вперёд! Например:

В старших классах часто приходится иметь дело с трехэтажными (а то и четырехэтажными!) дробями. Например:

Как эту дробь привести к приличному виду? Да очень просто! Использовать деление через две точки:

Но не забывайте о порядке деления! В отличие от умножения, здесь это очень важно! Конечно, 4:2, или 2:4 мы не спутаем. А вот в трёхэтажной дроби легко ошибиться. Обратите внимание, например:

В первом случае (выражение слева):

Во втором (выражение справа):

Чувствуете разницу? 4 и 1/9!

А чем задается порядок деления? Или скобками, или (как здесь) длиной горизонтальных черточек. Развивайте глазомер. А если нет ни скобок, ни черточек, типа:

то делим-умножаем по порядочку, слева направо !

И еще очень простой и важный приём. В действиях со степенями он вам ох как пригодится! Поделим единицу на любую дробь, например, на 13/15:

Дробь перевернулась! И так бывает всегда. При делении 1 на любую дробь, в результате получаем ту же дробь, только перевернутую.

Вот и все действия с дробями. Вещь достаточно простая, но ошибок даёт более, чем достаточно. Примите к сведению практические советы, и их (ошибок) будет меньше!

Практические советы:

1. Самое главное при работе с дробными выражениями - аккуратность и внимательность! Это не общие слова, не благие пожелания! Это суровая необходимость! Все вычисления на ЕГЭ делайте как полноценное задание, сосредоточенно и чётко. Лучше написать две лишние строчки в черновике, чем накосячить при расчёте в уме.

2. В примерах с разными видами дробей - переходим к обыкновенным дробям.

3. Все дроби сокращаем до упора.

4. Многоэтажные дробные выражения сводим к обыкновенным, используя деление через две точки (следим за порядком деления!).

5. Единицу на дробь делим в уме, просто переворачивая дробь.

Вот вам задания, которые нужно обязательно прорешать. Ответы даны после всех заданий. Используйте материалы этой темы и практические советы. Прикиньте, сколько примеров вы смогли решить правильно. С первого раза! Без калькулятора! И сделайте верные выводы...

Помните – правильный ответ, полученный со второго (тем более – третьего) раза – не считается! Такова суровая жизнь.

Итак, решаем в режиме экзамена ! Это уже подготовка к ЕГЭ, между прочим. Решаем пример, проверяем, решаем следующий. Решили все - проверили снова с первого по последний. И только потом смотрим ответы.

Вычислить:

Порешали?

Ищем ответы, которые совпадают с вашими. Я специально их в беспорядке записал, подальше от соблазна, так сказать... Вот они, ответы, через точку с запятой записаны.

0; 17/22; 3/4; 2/5; 1; 25.

А теперь делаем выводы. Если всё получилось - рад за вас! Элементарные вычисления с дробями - не ваша проблема! Можно заняться более серьёзными вещами. Если нет...

Значит, у вас одна из двух проблем. Или обе сразу.) Нехватка знаний и (или) невнимательность. Но... Это решаемые проблемы.

Если Вам нравится этот сайт...

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся - с интересом!)

можно познакомиться с функциями и производными.

В прошлый раз мы научились складывать и вычитать дроби (см. урок «Сложение и вычитание дробей »). Наиболее сложным моментом в тех действиях было приведение дробей к общему знаменателю.

Теперь настала пора разобраться с умножением и делением. Хорошая новость состоит в том, что эти операции выполняются даже проще, чем сложение и вычитание. Для начала рассмотрим простейший случай, когда есть две положительные дроби без выделенной целой части.

Чтобы умножить две дроби, надо отдельно умножить их числители и знаменатели. Первое число будет числителем новой дроби, а второе - знаменателем.

Чтобы разделить две дроби, надо первую дробь умножить на «перевернутую» вторую.

Обозначение:

Из определения следует, что деление дробей сводится к умножению. Чтобы «перевернуть» дробь, достаточно поменять местами числитель и знаменатель. Поэтому весь урок мы будем рассматривать в основном умножение.

В результате умножения может возникнуть (и зачастую действительно возникает) сократимая дробь - ее, разумеется, надо сократить. Если после всех сокращений дробь оказалась неправильной, в ней следует выделить целую часть. Но чего точно не будет при умножении, так это приведения к общему знаменателю: никаких методов «крест-накрест», наибольших множителей и наименьших общих кратных.

По определению имеем:

Умножение дробей с целой частью и отрицательных дробей

Если в дробях присутствует целая часть, их надо перевести в неправильные - и только затем умножать по схемам, изложенным выше.

Если в числителе дроби, в знаменателе или перед ней стоит минус, его можно вынести за пределы умножения или вообще убрать по следующим правилам:

1. Плюс на минус дает минус;
2. Минус на минус дает плюс.

До сих пор эти правила встречались только при сложении и вычитании отрицательных дробей, когда требовалось избавиться от целой части. Для произведения их можно обобщить, чтобы «сжигать» сразу несколько минусов:

1. Вычеркиваем минусы парами до тех пор, пока они полностью не исчезнут. В крайнем случае, один минус может выжить - тот, которому не нашлось пары;
2. Если минусов не осталось, операция выполнена - можно приступать к умножению. Если же последний минус не зачеркнут, поскольку ему не нашлось пары, выносим его за пределы умножения. Получится отрицательная дробь.

Задача. Найдите значение выражения:

Все дроби переводим в неправильные, а затем выносим минусы за пределы умножения. То, что осталось, умножаем по обычным правилам. Получаем:

Еще раз напомню, что минус, который стоит перед дробью с выделенной целой частью, относится именно ко всей дроби, а не только к ее целой части (это касается двух последних примеров).

Также обратите внимание на отрицательные числа: при умножении они заключаются в скобки. Это сделано для того, чтобы отделить минусы от знаков умножения и сделать всю запись более аккуратной.

Сокращение дробей «на лету»

Умножение - весьма трудоемкая операция. Числа здесь получаются довольно большие, и чтобы упростить задачу, можно попробовать сократить дробь еще до умножения . Ведь по существу, числители и знаменатели дробей - это обычные множители, и, следовательно, их можно сокращать, используя основное свойство дроби. Взгляните на примеры:

Задача. Найдите значение выражения:

По определению имеем:

Во всех примерах красным цветом отмечены числа, которые подверглись сокращению, и то, что от них осталось.

Обратите внимание: в первом случае множители сократились полностью. На их месте остались единицы, которые, вообще говоря, можно не писать. Во втором примере полного сокращения добиться не удалось, но суммарный объем вычислений все равно уменьшился.

Однако ни в коем случае не используйте этот прием при сложении и вычитании дробей! Да, иногда там встречаются похожие числа, которые так и хочется сократить. Вот, посмотрите:

Так делать нельзя!

Ошибка возникает из-за того, что при сложении в числителе дроби появляется сумма, а не произведение чисел. Следовательно, применять основное свойство дроби нельзя, поскольку в этом свойстве речь идет именно об умножении чисел.

Других оснований для сокращения дробей просто не существует, поэтому правильное решение предыдущей задачи выглядит так:

Правильное решение:

Как видите, правильный ответ оказался не таким красивым. В общем, будьте внимательны.

‌‌‌V‌ районная научно-практическая конференция исследовательских, проектных и творческих работ учащихся «Первые шаги в науке»

Исследовательская работа по теме:

«Сфера и шар – обычные геометрические тела».

Выполнил: ученик 9 класса МБОУ

«Кочетовская средняя общеобразовательная школа» Романов Дима.

Руководитель: учитель математики и физики Тремаскина В.С.

Введение ___________________________________________________________3

1. История изучения геометрических тел: шар, сфера_______________________3

2. Сфера и шар.

2.1. Понятие сферы и шара___________________________________________3-4

2.2. Уравнение сферы________________________________________________4

2.3. Взаимное расположение сферы и плоскости_________________________4-6

2.4. Касательная плоскость к сфере____________________________________6-7

2.5. Площадь сферы и объём шара____________________________________ 7

2.6. Получение сферы_______________________________________________ 7-8

2.7. Нахождение сферы и шара в природе______________________________ 9-13

2.8.Сфера и шар в повседневной жизни_________________________________14-15

2.9.Применение сферы и шара в архитектуре____________________________16-22

2.10. Применение сферы и шара в геодезии______________________________23

2.11Применение сферы и шара в астрономии и географии_________________24

2.12. Сфера и шар в искусстве_________________________________________25

Заключение___________________________________________________________25

Литература___________________________________________________________26

Актуальность выбранной темы.

На протяжении веков человечество не переставало пополнять свои научные знания в той или иной области наук. Множество ученых геометров, да и простых людей, интересовались такой фигурой как шар и его “оболочкой”, носящей название сфера. Многие реальные объекты в физике, астрономии, биологии и других естественных науках имеют форму шара. Поэтому вопросам изучения свойств шара отводилась в различные исторические эпохи и отводится в наше время значительная роль.

Цель исследования: изучить геометрические тела шар и сферу, рассмотреть их применение в разных областях науки, в повседневной жизни, в природе, создать презентацию «Сфера и шар – обычные геометрические тела».

Задачи:

1. Собрать материал о шаре и сфере используя различные источники информации, в том числе Интернет-ресурсы.

2. Систематизировать материал о шаре и сфере.

4. Создать презентацию«Сфера и шар – обычные геометрические тела ».

5. Представить работу на уроке геометрии при изучении темы «Сфера и шар».

Объект исследования : сфера и шар

Предмет исследования : элементы и свойства сферы и шара

Гипотеза: Шары нам нужны для того что бы делать наш мир более разнообразным и объёмным.

Методы: частично-поисковый, исследовательский, сравнительный анализ, синтез, практический.

Результат исследования: полученные знания нужны не только астрономам, штурманам морских кораблей, самолетов, космических кораблей, которые по звездам определяют свои координаты, но и строителям шахт, метрополитенов, тоннелей, архитекторам, а также при геодезических съёмках больших территорий поверхности Земли, когда становится необходимым учитывать её шарообразность, в повседневной жизни.

Научная новизна: теоретический материал представлен в форме доступной для понимания учащимися старших классов.

Практическая значимость: данный материал может использоваться в качестве основы для элективного курса в классах физико-математического профиля, на уроках при изучении тем «Сфера и шар».

Введение

На протяжении многих веков человечество не переставало пополнять свои научные знания в той или иной области науки. Стереометрия, как наука о фигурах в пространстве, неотъемлемо связана со многими из научных дисциплин. К таким дисциплинам относятся: математика, физика, информатика и программирование, а также химия и биология. В последних стоит проблема изучения микромира, который представляет собой сложнейшую комбинацию различных частиц в пространстве относительно друг друга. В архитектуре постоянно используются теоремы и следствия из стереометрии.

Множество учёных геометров, да и простых людей, интересовались такой фигурой как шар и его «оболочкой», носящей название сфера. Удивительно, но шар является единственным телом, обладающим большей площадью поверхности при объёме, равном объёму других сравниваемых тел, таких как куб, призма или прочие всевозможные многогранники. С шарами мы имеем дело ежедневно. К примеру, почти каждый человек пользуется шариковый ручкой в конец стержня которой вмонтирован металлический шар, вращающийся под действием сил трения между ним и бумагой и в процессе поворота на своей поверхности шар «выносит» очередную порцию чернил. В автомобильной промышленности изготавливаются шаровые опоры, являющиеся очень важной деталью в автомобиле и обеспечивающей правильный поворот колёс и устойчивость машины на дороге. Элементы машин, самолётов, ракет, мотоциклов, снарядов, плавательных судов, подвергающиеся постоянным воздействиям воды или воздуха, преимущественно имеют какие либо сферические поверхности, называемые обтекателями.

История изучения геометрических тел: шар, сфера

Шаром принято называть тело, ограниченное сферой, т.е. шар и сфера – это разные геометрические тела. Однако оба слова « шар» и « сфера» происходят от одного и того же греческого слова « сфайра» - мяч. При этом слово « шар» образовалось от перехода согласных сф в ш.

В XI книге «Начал» Евклид определяет шар как фигуру, описанную вращающимся около неподвижного диаметра полукругом. В древности сфера была в большом почёте. Астрономические наблюдения над небесным сводом неизменно вызывали образ сферы.

Сфера всегда широко применялась в различных областях науки и техники.

2.1. Понятие сферы и шара

Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки.

Тело, ограниченное сферой, называется шаром.

Данная точка называется центром сферы, а данное расстояние – радиусом сферы.

Отрезок, соединяющий две точки сферы и проходящий

через ее центр, называется диаметром сферы.

Центр, радиус, диаметр сферы называется также центром, радиусом и диаметром шара.

2.2. Уравнение сферы

Зададим прямоугольную систему координат О xyz

Построим сферу c центром в точке C (x 0;y 0;z 0)

и радиусом R

МС = (x – x 0 ) 2 + (y – y 0 ) 2 + (z – z 0 ) 2

МС = R , или МС2 = R2

следовательно уравнение

сферы имеет вид:

(x - x 0 ) 2 + (y - y 0 ) 2 + (z - z 0 ) 2 = R 2

2.3. Взаимное расположение сферы и плоскости

Дано:

Сфера радиуса R с центром С (х 0 ; у 0 ; z 0), точка М (х; у; z ) лежит на сфере.

Чему равно расстояние МС?

Т. к. МС = R , то

M

R

с

С С СС

Дано: плоскость α , сфера (С; R ),

d - расстояние от центра С до плоскости α .

Введем систему координат, где точка С (x 0 ;y 0 ;z 0). Составим уравнения сферы и плоскости α .

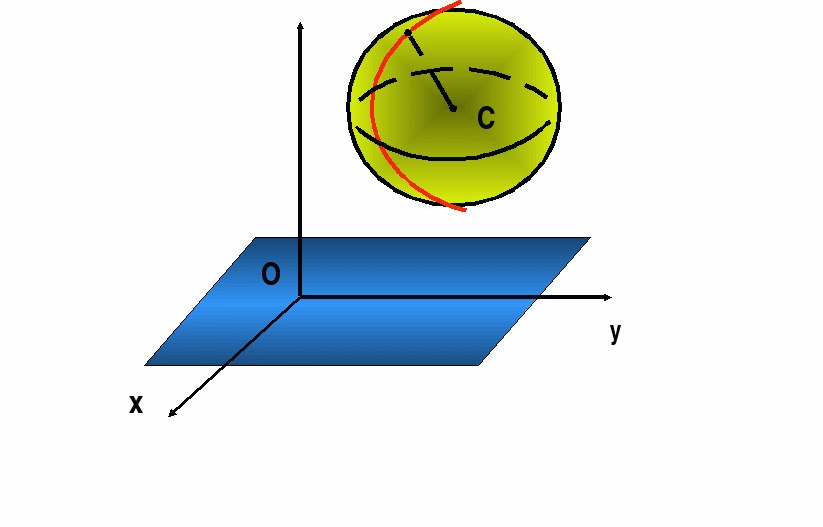
z

П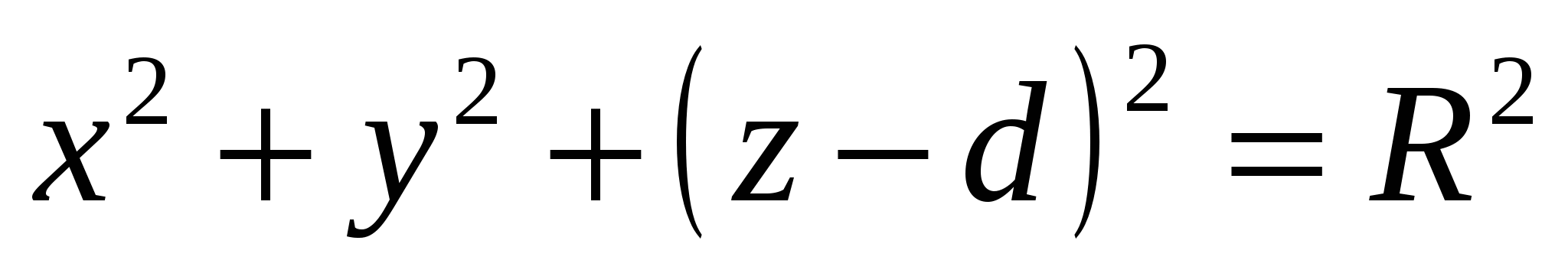
усть точка С лежит на оси z . Тогда ее координаты (0; 0; d ).

Уравнение сферы:

Уравнение плоскости α : z = 0

Исследуем систему уравнений:

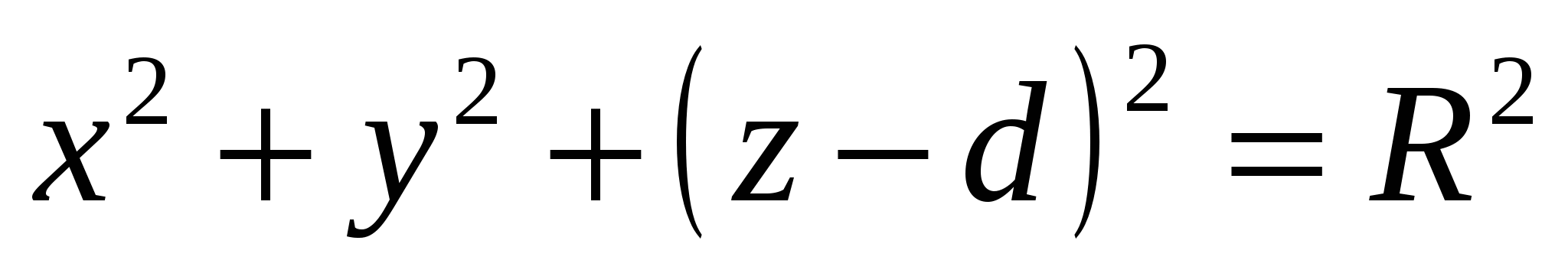
z = 0

Тогда

В зависимости от соотношения d и R возможны 3 случая…

1
) d < R .

Тогда

уравнение окружности (О; r )

Сечение сферы плоскостью – окружность

2
) d = R .

Тогда

Верно при

х = 0 и у = 0

Сфера и плоскость имеют одну общую точку.

3
) d > R .

Тогда

не имеет решений.

Сфера и плоскость не имеют общих точек.

2.4. Касательная плоскость к сфере

Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка называется точкой касания плоскости и сферы.

Теорема. Радиус сферы, проведенный в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.

Дано: сфера с центром О и радиусом R , α - касательная к сфере в точке А плоскость.

Доказать: OA а .

Доказательство: Пусть OA не перпендикулярна плоскости а , тогда OA является наклонной к плоскости, значит, расстояние от центра до плоскости d < R . Т.е. сфера должна пересекаться с плоскостью по окружности, но это не удовлетворяет условию теоремы. Значит, OA а .

Докажем обратную теорему.

Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащий на сфере, то эта плоскость является касательной к сфере.

Дано: сфера с центром О и радиусом OA , а, OA а .

Доказать: а – касательная плоскость.

Доказательство: Т.к. OA а , то расстояние от центра сферы до плоскости равно радиусу. Значит, сфера и плоскость имеют одну общую точку. По определению, плоскость является касательной к сфере.

2.5. Площадь сферы и объём шара

и шара радиуса определяются формулами:

Доказательство

Возьмём четверть круга радиуса R с центром в точке . Уравнение окружности этого круга: , откуда .

Функция непрерывная, возрастающая, неотрицательная. При вращении четверти круга вокруг оси Ox образуется полушар, следовательно:

Откуда Ч. т. д.

Доказательство

Ч. т. д.

Часть шара, [ ] осекаемая от него какой-нибудь плоскостью, называется шаровым или сферическим сегментом. Основанием шарового сегмента называется кругABCD . Высотой шарового сегмента называется отрезок NM , т.е. длина перпендикуляра, восстановленного из центраN основания до пересечения с поверхностью шара. ТочкаM называется вершиной шарового сегмента.

Объем шарового сегмента выражается формулой:

V = π h 2 ( R − 1/3 h)

Шаровой слой - это часть шара [ ], заключенная между двумя секущими параллельными плоскостями. Шаровой пояс или Шаровая зона - это кривая поверхность шарового слоя. Круги ABC и DEF это основания шарового пояса. Расстояние между основаниямиON - это высота шарового слоя.

Объем шарового слоя выражается формулой:

V = 1/6 π h 3 + 1/2 π( r 1 2 + r 2 2 ) h

Шаровой сектор - это часть шара [ ], ограниченная кривой поверхностью шарового сегмента и конической поверхностью основанием которой служит основание сегмента, а вершиной - центр шара.

Объем шарового сектора равен , основание которой имеет ту же площадь, что и вырезаемая сектором часть шаровой поверхности, а высота равна радиусу

V = 1/3 R S = 2/3 π R 2 h

2.6. Получение сферы

Сферу можно получить вращением полуокружности АСВ вокруг диаметра АВ

2.7. Нахождение сферы и шара в природе

Загадки природы - Шары-послания. Эти загадочные каменные образования идеально круглой формы были обнаружены в конце 1940-х годов в джунглях центрально американской Республики Коста-Рика. Шары имеют размеры от 10 см до 3-4 метров в диаметре. При аэросъемке выяснилось, что они разбросаны по поверхности земли не случайно, а составляют геометрические фигуры. Возможно даже, что шары не разбросаны, а разложены в виде огромной звездной карты; каждый шар - это звезда с соответствующим описанием.

Среди гипотез происхождения шаров есть только экзотические версии: от пришельцев до скульпторов Атлантиды. Есть версия и о том, что шары вырезали (в расчете на будущие дивиденды от туризма) скучающие нацистские мигранты, наводнившие Латинскую Америку после краха «третьего рейха». Естественными причинами объяснить обилие шаров и странные рисунки на них не удалось. В Казахстане при разработке песчаного карьера на достаточно большой глубине также были обнаружены несколько крупных экземпляров таких валунов… Об этой находке сообщала комиссия «Феномен»; увы, фотографий находок не сохранилось.

Хрустальный шарик. Макросъёмка. На ветке какого-то дерева лежит шар из стекла, в нём отражается окружающая его природа. Очень симпатичные жёлтые цветочки и зелёная сочная трава.

Светящиеся шары

на фото в местах силы - результат распада урана или плазмоидная форма жизни?

Храм Гроба Господня и другие места Израиля

И
нтересное природное явление на берегу мичиганского озера сформировались тысячи правильных ледяных шаров

Морские водоросли в виде необычных шаров

Странные шары появились на побережье Хэмптона, что на восточном побережье США, в июне 2002 года. Приливная волна стала выносить несметное число таких зеленоватых шаров - мягких, отдаленно напоминающих губку и размером с мячик для тенниса или гольфа. На расстоянии примерно 300 метров или больше весь песчаный пляж буквально был усеян такими шарами. Тут же начались споры- что это и откуда? В дебаты оказались вовлеченными и биологи маринисты, и отдыхающие на пляже, и случайные прохожие. Прежде никто не видел здесь ничего подобного.

Природа боится симметрии, природа не знает идеальных геометрических фигур. Зато человек может заставить природу приобрести эти чуждые ей формы. Наглядный пример тому - творчество корейского художника Lee Jae-Hyo, который создает из стволов деревьев идеальные сферы

Т

ысячи небольших фиолетовых шариков странным образом оказались в центре пустыни в штате Аризона, США. Жители города Тусон Джеральдина Варгас и ее муж обнаружили необъяснимое скопление непонятных шаров пару недель назад во время прогулки по окрестностям. "Мы фотографировали природу пустыни, когда натолкнулись на это странное место... не понимаю, как мы сразу его не заметили? - рассказала Джеральдина журналистам. – Оно просто искрилось на солнце". Фотографы отправили фото со странными объектами своей знакомой зоологу, но она не смогла сказать, что же это такое, у нее даже не было никаких предположений на этот счет.

Шары из минералов.

Аметист.Бразилия.

Горный хрусталь.Южный.Челяб.обл.Продан.

Амазонит.Кольский п-ов.Продан.

2.8 Сфера и шар в повседневной жизни

Н
а геометрический шар похожи глобус, футбольный мяч, новогодние игрушки.

Шар из пенопласта своими руками

Зорбинг (zorbing) – это один из самых модных экстремальных развлечений на сегодняшний день. Зорбинг позволит вам испытать новые, необычно яркие и мощные ощущения и встряхнуться от обыденности повседневной жизни.

Что такое шар Зорб

Зорб (ZORB) представляет из себя прозрачную сферу (шар) диаметром 3,2 метра внутри которой находится сфера диаметром 1,8 метра, в которой находится зорбонавт (пассажир зорба ). Пространство между этими сферами наполняется воздухом, давлением которого сферы распираются между собой, а стропами, наоборот, удерживаются. Такая система очень хорошо амортизирует, сглаживает неровности трассы и делает катание безопасным.

2.9.Применение сферы и шара в архитектуре

Такой дом называется ВИГВАМ . Такие дома строят ИНДЕЙЦЫ .

Шары и полусферы из нержавеющей стали

Фонтан "Вращающийся шар " в Санкт-

Петербурге -

Современные дома

А если дом не просто на дереве, а ещё и в форме шара.

Это поселок из самых настоящих круглых домов .

С
овременные круглые дома

Монреальская Биосфера - выставочный павильон США на Экспо-67 в Канаде,

созданная архитектором Ричардом Фуллером.

Отель в виде прозрачных шаров

В
о французском городе Рубе (Roubaix) в одном из парков открыли портативные гостиничные номера Hotel Bolha. Сделали это специально для людей, которые даже в центре городских джунглей желают побыть ближе к природе. Концепцию пузыря придумал дизайнер Пьер Стефан Дюма. Такая продвинутая конструкция была создана с целью временного присоединения постояльцев к неизведанному. Ведь не многие могут себе позволить поспать под круглым потолком.

Платье из шаров.

Дачный офис Скоро весна (а там и лето) и многие начнут ездить на дачу отдыхать.
Но иногда на даче нужно поработать (чтоб тебя!). Нет места где уединится?
Можно вот в таком вот небольшом шарообразном сооружение «Archipod»:

ЭНЕРГОЭФФЕКТИВНОСТЬ в архитектуре . Умный Дом - молекула.

В парке науки и техники La Vilette, построенном на месте скотобойни на восточной окраине Парижа, бросается в глаза гигантский шар, в зеркальной поверхности которого отражается парижское небо и окружающий пейзаж. На сегодняшний день это здание считается самым совершенным в мире сооружением сферической формы. Парижане называют его «Жеод» (Gеode). Это – панорамный

кинотеатр с самым большим в Европе экраном . дом-шар зеркало

Такие шары из ниток можно просто подвесить к веткам дерева, если ваш праздник проходит на природе, или к потолку. А также ими можно оформить банкетный стол, дополнив композицию свечами и цветами.

2.10. Применение сферы и шара в геодезии.

Картографические проекции

отображения всей поверхности земного эллипсоида (См. ) или какую-либо её части на плоскость, получаемые в основном с целью построения карты.

Масштаб. К. п. строятся в определённом масштабе. Уменьшая мысленно земной эллипсоид в М раз, например в 10 000 000 раз, получают его геометрическую модель - , изображение которого уже в натуральную величину на плоскости даёт карту поверхности этого эллипсоида. Величина 1: М (в примере 1: 10 000 000) определяет главный, или общий, масштаб карты. Т. к. поверхности эллипсоида и шара не могут быть развёрнуты на плоскость без разрывов и складок (они не принадлежат к классу развёртывающихся поверхностей (См. )), любой К. п. присущи искажения длин линий, углов и т.п., свойственные всякой карте. Основной характеристикой К. п. в любой её точке является частный масштаб μ. Это - величина, обратная отношению бесконечно малого отрезка ds на земном эллипсоиде к его изображению dσ на плоскости: μ min ≤ μ ≤ μ max , и равенство здесь возможно лишь в отдельных точках или вдоль некоторых линий на карте. Т. о., главный масштаб карты характеризует её только в общих чертах, в некотором осреднённом виде. Отношение μ/М называют относительным масштабом, или увеличением длины, разность М = 1.

1. Сети сферических координатных линий.

2.11. Применение сферы и шара в астрономии и географии.

Сфера и шар, так же как окружность и круг, рассматривали еще в глубокой древности. Открытие шарообразности Земли, появление представлений о небесной сфере дали толчок к развитию специальной науки – СФЕРИКИ, изучающей расположенные на сфере фигуры.

Осуществляя кругосветные путешествия, мореплаватели заметили, что при возвращении в то же место наблюдается потеря или выигрыш целых суток, что было бы совершенно невозможно, если бы Земля имела форму диска.

Итак, доказательствами шарообразности Земли в настоящее время служат:

Всегда кругообразная фигура горизонта в океане и в открытых низменностях или плоскогорьях;

Кругосветные путешествия.

Постепенное приближение или удаление предметов;

И
зучая различные географические карты, мы обнаружили, что в географии есть географические названия, связанные с шаром. Например, между Северным и Южными островами Новой Земли есть пролив, который соединяет Баренцево и Карское моря, который называется Маточкин Шар, или пролив между берегами острова Вайгач и материком Евразии – Югорский Шар. Мы думаем, что эти проливы названы шарами в силу того, что их размеры, форма дна напоминают шаровую поверхность.

2.12. Сфера и шар в искусстве

Математика Эшера

Кроме того, «игрой» с логикой пространства являются картины Эшера, на которых изображены различные «невозможные фигуры»; Эшер изображал их как отдельно, так и в сюжетных литографиях и гравюрах

Три сферы. 1946

Рука с отражающей сферой. 1935

Заключение

Думаю, что собранный мной материал и знания, полученные в ходе проделанной работы можно использовать на уроках геометрии, труда, в повседневной жизни, в качестве основы для элективного курса в классах физико-математического профиля, а так же на внеклассных занятиях для расширения кругозора учеников.

Литература

Адамар Ж. Элементарная геометрия. Ч.2. М. Учпедгиз, 1958. Андреев

Атанасян Л.С. Геометрия. Ч.2. – М: Просвещение, 1987. – 352с.

Базылев В.Т. Геометрия. М: Просвещение, 1975.

Базылев В.Т. Сборник задач по геометрии. М: Просвещение, 1980. -240с.

Егоров И.П. Геометрия. – М: Просвещение, 1979. – 256с.

Егоров И.П. Основания геометрии. – М: Просвещение, 1984. – 144с.

Задачник «Кванта»: Математика. Часть 1. / Под ред. Н.Б. Васильева. М: 1997.

Розенфельд Б.А. История неевклидовой геометрии. Развитие понятия о геометрическом пространстве. М. Наука., 1976. – 408с.

Энциклопедия элементарной математики. Кн.4 – Геометрия. М., 1963.

10.Интернет-ресурсы.

Сфера - это одно из первых тел, обладающих высокой симметрией, свойства которого изучают в школьном курсе геометрии. В данной статье рассматривается формула сферы, ее отличие от шара, а также приводится расчет площади поверхности нашей планеты.

Сфера: понятие в геометрии

Чтобы лучше понять формулу поверхности, которая будет дана ниже, необходимо познакомиться с понятием сферы. В геометрии она представляет собой трехмерное тело, которое заключает в себе некоторый объем пространства. Математическое определение сферы следующее: это совокупность точек, которые лежат на определенном одинаковом расстоянии от одной фиксированной точки, называемой центром. Отмеченное расстояние - это радиус сферы, который обозначается r или R и измеряется в метрах (километрах, сантиметрах и других единицах длины).

На рисунке ниже приведена описанная фигура. Линии показывают контуры ее поверхности. Черная точка - центр сферы.

Получить эту фигуру можно, если взять окружность и начать ее вращать вокруг любой из осей, проходящей через диаметр.

Сфера и шар: в чем разница и в чем сходство?

Часто школьники путают эти две фигуры, которые внешне похожи друг на друга, но обладают совершенно разными физическими свойствами. Сфера и шар в первую очередь отличаются своей массой: сфера - это бесконечно тонкий слой, шар же - это объемное тело конечной плотности, которая одинакова во всех его точках, ограниченных сферической поверхностью. То есть шар обладает конечной массой и является вполне реальным объектом. Сфера - это фигура идеальная, не имеющая массы, которая в действительности не существует, но она является удачной идеализацией в геометрии при изучении ее свойств.

Примерами реальных объектов, форма которых практически соответствует сфере, являются новогодняя игрушка в виде шарика для украшения елки или мыльный пузырь.

Что касается сходства между рассматриваемыми фигурами, то можно назвать следующие их признаки:

• обе они обладают одинаковой симметрией;
• для обеих формула площади поверхности является одинаковой, более того, они обладают равной площадью поверхности, если их радиусы равны;
• обе фигуры при равных радиусах занимают одинаковый объем в пространстве, только шар его заполняет полностью, а сфера лишь ограничивает своей поверхностью.

Сфера и шар равного радиуса приведены на рисунке ниже.

Заметим, что шар, так же как и сфера, является телом вращения, поэтому его можно получить, если вращать вокруг диаметра круг (не окружность!).

Элементы сферы

Так называются геометрические величины, знание которых позволяет описать либо всю фигуру, либо отдельные ее части. Основными ее элементами являются следующие:

• Радиус r, который уже был упомянут ранее. Он является расстоянием от центра фигуры до сферической поверхности. По сути, это единственная величина, которая описывает все свойства сферы.
• Диаметр d, или D. Это отрезок, концы которого лежат на сферической поверхности, а середина проходит через центральную точку фигуры. Диаметр сферы можно провести бесконечным числом способов, но все полученные отрезки будут иметь одинаковую длину, которая равна удвоенному радиусу, то есть D = 2*R.
• Площадь поверхности S - двумерная характеристика, формула для которой будет приведена ниже.
• Связанные со сферой трехмерные углы измеряются в стерадианах. Один стерадиан - это угол, вершина которого лежит в центре сферы, и который опирается на часть сферической поверхности, имеющей площадь R 2 .

Геометрические свойства сферы

Из приведенного описания этой фигуры можно самостоятельно догадаться об этих свойствах. Они следующие:

• Любая прямая, которая пересекает сферу и проходит через ее центр, является осью симметрии фигуры. Поворот сферы вокруг этой оси на любой угол переводит ее в саму себя.
• Плоскость, которая пересекает рассматриваемую фигуру через ее центр, делит сферу на две равные части, то есть является плоскостью отражения.

Площадь поверхности фигуры

Эта величина обозначается латинской буквой S. Формула вычисления площади сферы имеет следующий вид:

S = 4*pi*R 2 , где pi ≈ 3,1416.

Формула демонстрирует, что площадь S может быть вычислена при условии знания радиуса фигуры. Если же известен ее диаметр D, тогда формулу сферы можно записать так:

Иррациональное число pi, для которого приведены четыре знака после запятой, в ряде математических расчетов можно использовать с точностью до сотых, то есть 3,14.

Любопытно также рассмотреть вопрос, скольким стерадианам соответствует вся поверхность рассматриваемой фигуры. Исходя из определения этой величины, получаем:

Ω = S/R 2 = 4*pi*R 2 /R 2 = 4*pi стерадиан.

Для вычисления любого объемного угла следует в выражение выше подставить соответствующее значение площади S.

Поверхность планеты Земля

Формулу сферы можно применить для определения на которой мы живем. Перед тем как приступать к вычислениям, следует сделать пару оговорок:

• Во-первых, Земля не обладает идеальной сферической поверхностью. Ее экваториальный и полярный радиусы равны 6378 км и 6357 км соответственно. Отличие между этими цифрами не превышает 0,3%, поэтому для расчета можно взять средний радиус 6371 км.
• Во-вторых, рельеф является трехмерным, то есть на ней имеются впадины и горы. Эти характерные особенности планеты приводят к увеличению ее площади поверхности, тем не менее, в расчете их учитывать не будем, поскольку даже самая большая гора, Эверест, составляет 0,1% от земного радиуса (8,848/6371).

Используя формулу сферы, получаем:

S = 4*pi*R 2 = 4*3,1416*6371 2 ≈ 510,066 млн. км 2 .

Россия, по официальным данным, занимает площадь 17,125 млн км 2 , что составляет 3,36% от поверхности планеты. Если же учесть, что к суше относятся лишь 150,387 млн км 2 , тогда площадь нашей страны составит 11,4% от всей территории, не покрытой водой.