heim » Wohnungsgestaltung » Lokale Maximum- und Minimumdefinition. Extremum der Funktion. Beispiele für Problemlösungen

Lokale Maximum- und Minimumdefinition. Extremum der Funktion. Beispiele für Problemlösungen

Der Extrempunkt einer Funktion ist der Punkt im Definitionsbereich der Funktion, an dem der Wert der Funktion ein Minimum annimmt Maximalwert. Die Werte der Funktion an diesen Punkten werden Extrema (Minimum und Maximum) der Funktion genannt.

Definition. Punkt X1 Funktionsdomäne F(X) wird genannt Maximalpunkt der Funktion , wenn der Wert der Funktion an dieser Stelle ist mehr Werte Funktion an Punkten, die hinreichend nahe bei ihr liegen und sich rechts und links davon befinden (d. h. die Ungleichung). F(X0 ) > F(X 0 + Δ X) X1 maximal.

Definition. Punkt X2 Funktionsdomäne F(X) wird genannt Minimalpunkt der Funktion, wenn der Wert der Funktion an diesem Punkt kleiner ist als die Werte der Funktion an Punkten, die ausreichend nahe daran liegen, rechts und links davon liegen (d. h. die Ungleichung gilt). F(X0 ) < F(X 0 + Δ X) ). In diesem Fall sagen wir, dass die Funktion den Punkt hat X2 Minimum.

Sagen wir Punkt X1 - Maximalpunkt der Funktion F(X). Dann im Intervall bis X1 Funktion erhöht, also die Ableitung der Funktion Über Null (F "(X) > 0 ) und im Intervall danach X1 die Funktion nimmt also ab, Ableitung einer Funktion weniger als Null ( F "(X) < 0 ). Тогда в точке X1

Nehmen wir auch an, dass der Punkt X2 - Minimalpunkt der Funktion F(X). Dann im Intervall bis X2 Die Funktion nimmt ab und die Ableitung der Funktion ist kleiner als Null ( F "(X) < 0 ), а в интервале после X2 Die Funktion nimmt zu und die Ableitung der Funktion ist größer als Null ( F "(X) > 0 ). In diesem Fall auch an der Stelle X2 Die Ableitung der Funktion ist Null oder existiert nicht.

Satz von Fermat ( notwendiges Zeichen Existenz eines Extremums der Funktion). Wenn der Punkt X0 - Extrempunkt der Funktion F(X), dann ist die Ableitung der Funktion an diesem Punkt gleich Null ( F "(X) = 0 ) oder existiert nicht.

Definition. Es werden die Punkte aufgerufen, an denen die Ableitung einer Funktion Null ist oder nicht existiert kritische Punkte .

Beispiel 1. Betrachten wir die Funktion.

Am Punkt X= 0 ist die Ableitung der Funktion Null, also der Punkt X= 0 ist der kritische Punkt. Allerdings nimmt sie, wie im Diagramm der Funktion zu sehen ist, über den gesamten Definitionsbereich, also den Punkt, zu X= 0 ist nicht der Extrempunkt dieser Funktion.

Somit sind die Bedingungen, dass die Ableitung einer Funktion an einem Punkt gleich Null ist oder nicht existiert, notwendige Bedingungen für ein Extremum, aber nicht ausreichend, da außer der Funktion auch andere Beispiele für Funktionen angegeben werden können, für die diese Bedingungen erfüllt sind hat am entsprechenden Punkt kein Extremum. Deshalb Es müssen ausreichende Beweise vorliegen Dies ermöglicht die Beurteilung, ob an einem bestimmten kritischen Punkt ein Extremum vorliegt und um welche Art von Extremum es sich handelt – Maximum oder Minimum.

Satz (das erste hinreichende Zeichen für die Existenz eines Extremums einer Funktion). Kritischer Punkt X0 F(X) Wenn beim Durchlaufen dieses Punktes die Ableitung der Funktion das Vorzeichen ändert und wenn sich das Vorzeichen von „Plus“ nach „Minus“ ändert, dann handelt es sich um einen Maximalpunkt, und wenn von „Minus“ nach „Plus“, dann es ist ein Mindestpunkt.

Wenn in der Nähe des Punktes X0 , links und rechts davon behält die Ableitung ihr Vorzeichen, das bedeutet, dass die Funktion in einer bestimmten Umgebung des Punktes entweder nur abnimmt oder nur zunimmt X0 . In diesem Fall an der Stelle X0 es gibt kein Extrem.

Also, Um die Extrempunkte der Funktion zu bestimmen, müssen Sie Folgendes tun :

Finden Sie die Ableitung der Funktion.
Setzen Sie die Ableitung mit Null gleich und bestimmen Sie die kritischen Punkte.
Markieren Sie im Geiste oder auf dem Papier kritische Punkte Zahlenachse und bestimmen Sie die Vorzeichen der Ableitung der Funktion in den resultierenden Intervallen. Wenn sich das Vorzeichen der Ableitung von „Plus“ nach „Minus“ ändert, ist der kritische Punkt der Maximalpunkt, und wenn von „Minus“ nach „Plus“, dann der Minimalpunkt.
Berechnen Sie den Wert der Funktion an den Extrempunkten.

Beispiel 2. Finden Sie die Extrema der Funktion .

Lösung. Finden wir die Ableitung der Funktion:

Setzen wir die Ableitung mit Null gleich, um die kritischen Punkte zu finden:

Denn für alle Werte von „x“ gibt es keinen Nenner gleich Null, dann setzen wir den Zähler mit Null gleich:

Ich habe einen kritischen Punkt X= 3 . Bestimmen wir das Vorzeichen der Ableitung in den durch diesen Punkt begrenzten Intervallen:

im Bereich von minus unendlich bis 3 - ein Minuszeichen, d. h. die Funktion nimmt ab,

Im Intervall von 3 bis plus Unendlich gibt es ein Pluszeichen, das heißt, die Funktion nimmt zu.

Das heißt, Punkt X= 3 ist der Mindestpunkt.

Lassen Sie uns den Wert der Funktion am Minimalpunkt ermitteln:

Somit wird der Extrempunkt der Funktion gefunden: (3; 0) und es ist der Minimalpunkt.

Satz (das zweite hinreichende Zeichen für die Existenz eines Extremums einer Funktion). Kritischer Punkt X0 ist der Extrempunkt der Funktion F(X), wenn die zweite Ableitung der Funktion an dieser Stelle ungleich Null ist ( F ""(X) ≠ 0 ), und wenn die zweite Ableitung größer als Null ist ( F ""(X) > 0 ), dann der Maximalpunkt, und wenn die zweite Ableitung kleiner als Null ist ( F ""(X) < 0 ), то точкой минимума.

Hinweis 1. Wenn an der Stelle X0 Wenn sowohl die erste als auch die zweite Ableitung verschwinden, ist es zu diesem Zeitpunkt unmöglich, das Vorhandensein eines Extremums anhand des zweiten hinreichenden Kriteriums zu beurteilen. In diesem Fall müssen Sie das erste ausreichende Kriterium für das Extremum einer Funktion verwenden.

Bemerkung 2. Das zweite ausreichende Kriterium für das Extremum einer Funktion ist selbst dann nicht anwendbar, wenn die erste Ableitung an einem stationären Punkt nicht existiert (dann existiert auch die zweite Ableitung nicht). In diesem Fall müssen Sie auch das erste ausreichende Vorzeichen eines Extremums einer Funktion verwenden.

Lokale Natur der Extrema der Funktion

Aus den obigen Definitionen folgt, dass das Extremum der Funktion lokaler Natur ist – es ist das größte und kleinster Wert Funktionen im Vergleich zu nahegelegenen Werten.

Nehmen wir an, Sie betrachten Ihre Einnahmen über einen Zeitraum von einem Jahr. Wenn Sie im Mai 45.000 Rubel, im April 42.000 Rubel und im Juni 39.000 Rubel verdient haben, dann ist der Mai-Verdienst das Maximum der Verdienstfunktion im Vergleich zu nahegelegenen Werten. Aber im Oktober haben Sie 71.000 Rubel verdient, im September 75.000 Rubel und im November 74.000 Rubel, sodass der Oktoberverdienst das Minimum der Verdienstfunktion im Vergleich zu nahegelegenen Werten darstellt. Und Sie können leicht erkennen, dass das Maximum der Werte von April-Mai-Juni unter dem Minimum von September-Oktober-November liegt.

Im Allgemeinen kann eine Funktion in einem Intervall mehrere Extrema haben, und es kann sich herausstellen, dass ein Minimum der Funktion größer als ein Maximum ist. Für die in der Abbildung oben gezeigte Funktion gilt also .

Das heißt, man sollte nicht denken, dass das Maximum und das Minimum einer Funktion deren größter bzw. kleinster Wert im gesamten betrachteten Segment sind. Am Maximalpunkt hat die Funktion den größten Wert nur im Vergleich zu den Werten, die sie an allen Punkten hat, die ausreichend nahe am Maximalpunkt liegen, und am Minimalpunkt hat sie den kleinsten Wert nur im Vergleich zu diesen Werten dass es an allen Punkten ausreichend nahe am Minimalpunkt liegt.

Daher können wir das obige Konzept der Extrempunkte einer Funktion klarstellen und Minimalpunkte als lokale Minimalpunkte und Maximalpunkte als lokale Maximalpunkte bezeichnen.

Wir suchen gemeinsam nach den Extrema der Funktion

Beispiel 3.

Lösung: Die Funktion ist auf dem gesamten Zahlenstrahl definiert und stetig. Seine Ableitung existiert auch auf dem gesamten Zahlenstrahl. Deshalb in in diesem Fall Kritische Punkte sind nur diejenigen, an denen, d.h. , von wo und . Kritische Punkte und teilen Sie den gesamten Definitionsbereich der Funktion in drei Intervalle der Monotonie auf: . Wählen wir in jedem von ihnen einen Kontrollpunkt aus und ermitteln wir das Vorzeichen der Ableitung an diesem Punkt.

Für das Intervall kann der Kontrollpunkt sein: finden. Wenn wir einen Punkt im Intervall nehmen, erhalten wir, und wenn wir einen Punkt im Intervall nehmen, haben wir. Also, in den Intervallen und und im Intervall. Nach dem ersten ausreichendes Zeichen Es gibt kein Extremum, es gibt kein Extremum an dem Punkt (da die Ableitung ihr Vorzeichen im Intervall behält) und an dem Punkt hat die Funktion ein Minimum (da die Ableitung beim Durchgang durch diesen Punkt ihr Vorzeichen von Minus nach Plus ändert). Finden wir die entsprechenden Werte der Funktion: , a . Im Intervall nimmt die Funktion ab, da in diesem Intervall , und im Intervall nimmt sie zu, da in diesem Intervall .

Um den Aufbau des Graphen zu verdeutlichen, ermitteln wir seine Schnittpunkte mit den Koordinatenachsen. Wenn wir eine Gleichung erhalten, deren Wurzeln und sind, werden also zwei Punkte (0; 0) und (4; 0) des Funktionsgraphen gefunden. Aus allen erhaltenen Informationen erstellen wir ein Diagramm (siehe Anfang des Beispiels).

Beispiel 4. Finden Sie die Extrema der Funktion und erstellen Sie ihren Graphen.

Der Definitionsbereich einer Funktion ist der gesamte Zahlenstrahl mit Ausnahme des Punktes, d. h. .

Um die Studie zu verkürzen, können Sie die Tatsache nutzen, dass diese Funktion gerade ist, da . Daher ist sein Graph symmetrisch zur Achse Oy und die Studie kann nur für das Intervall durchgeführt werden.

Die Ableitung finden und kritische Punkte der Funktion:

1) ;

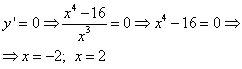2) ,

Da die Funktion an diesem Punkt jedoch eine Diskontinuität aufweist, kann es sich nicht um einen Extrempunkt handeln.

Auf diese Weise, gegebene Funktion hat zwei kritische Punkte: und . Unter Berücksichtigung der Parität der Funktion prüfen wir nur den Punkt anhand des zweiten ausreichenden Kriteriums für ein Extremum. Dazu ermitteln wir die zweite Ableitung und bestimmen Sie sein Vorzeichen bei: Wir erhalten . Da und ist es der Minimalpunkt der Funktion und .

Um ein vollständigeres Bild des Graphen einer Funktion zu erhalten, wollen wir ihr Verhalten an den Grenzen des Definitionsbereichs herausfinden:

(Hier zeigt das Symbol den Wunsch an X von rechts auf Null und X bleibt positiv; bedeutet in ähnlicher Weise Streben X von links auf Null und X bleibt negativ). Also wenn, dann. Als nächstes finden wir

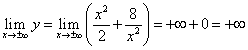diese. wenn, dann .

Der Graph einer Funktion hat keine Schnittpunkte mit den Achsen. Das Bild befindet sich am Anfang des Beispiels.

Wir suchen weiterhin gemeinsam nach Extrema der Funktion

Beispiel 8. Finden Sie die Extrema der Funktion.

Lösung. Finden wir den Definitionsbereich der Funktion. Da die Ungleichung erfüllt sein muss, erhalten wir aus .

Finden wir die erste Ableitung der Funktion:

Finden wir die kritischen Punkte der Funktion.

Für eine Funktion f(x) von vielen variabler Punkt x ist ein Vektor, f'(x) ist der Vektor der ersten Ableitungen (Gradient) der Funktion f(x), f ′ ′(x) ist die symmetrische Matrix der zweiten partiellen Ableitungen (Hessische Matrix – Hessisch) von die Funktion f(x).
Für die Funktion vieler Bedingungsvariablen Optimalitäten werden wie folgt formuliert.
Eine notwendige Voraussetzung für lokale Optimalität. Sei f(x) im Punkt x * R n differenzierbar. Wenn x * ein lokaler Extrempunkt ist, dann ist f’(x *) = 0.
Nach wie vor werden Punkte, die Lösungen eines Gleichungssystems sind, als stationär bezeichnet. Die Natur des stationären Punktes x * hängt mit dem bestimmten Vorzeichen der Hesse-Matrix f′ ′(x) zusammen.
Das Vorzeichen der Matrix A hängt von den Vorzeichen der quadratischen Form Q(α)= ab< α A, α >für alle ungleich Null α∈R n .
Hier und weiter bezeichnet durch Skalarprodukt Vektoren x und y. A-Priorat,

Eine Matrix A ist positiv (nicht negativ) definit, wenn Q(α)>0 (Q(α)≥0) für alle α∈R n ungleich Null; negativ (nicht positiv) definit wenn Q(α)<0 (Q(α)≤0) при всех ненулевых α∈R n ; неопределенной, если Q(α)>0 für ein von Null verschiedenes α∈R n und Q(α)<0 для остальных ненулевых α∈R n .
Ausreichende Bedingung für lokale Optimalität. Sei f(x) im Punkt x * R n zweimal differenzierbar und f’(x *)=0, d.h. x * − stationären Punkt. Wenn dann die Matrix f′′(x *) positiv (negativ) definit ist, dann ist x * ein lokaler minimaler (maximaler) Punkt; Wenn die Matrix f′′(x *) undefiniert ist, dann ist x * ein Sattelpunkt.
Wenn die Matrix f''(x *) nicht negativ (nicht positiv) definit ist, dann erfordert die Bestimmung der Natur des stationären Punktes x * die Untersuchung von Ableitungen höherer Ordnung.
Zur Überprüfung des Vorzeichens einer Matrix wird in der Regel das Sylvester-Kriterium verwendet. Nach diesem Kriterium ist eine symmetrische Matrix A genau dann positiv definit, wenn alle ihre Winkelminorwerte positiv sind. In diesem Fall ist der Nebenwinkel der Matrix A die Determinante einer Matrix, die aus Elementen der Matrix A aufgebaut ist, die sich am Schnittpunkt von Zeilen und Spalten mit denselben (und ersten) Zahlen befinden. Um die symmetrische Matrix A auf negative Bestimmtheit zu prüfen, müssen Sie die Matrix (−A) auf positive Bestimmtheit prüfen.
Der Algorithmus zur Bestimmung lokaler Extrempunkte einer Funktion vieler Variablen lautet also wie folgt.
1. Finden Sie f′(x).
2. Das System wird gelöst

Als Ergebnis werden stationäre Punkte x i berechnet.
3. Finden Sie f''(x) und setzen Sie i=1.
4. Finden Sie f''(x i)
5. Die Winkelminorwerte der Matrix f''(x i) werden berechnet. Wenn nicht alle Winkelminorwerte ungleich Null sind, erfordert die Bestimmung der Natur des stationären Punktes x i die Untersuchung von Ableitungen höherer Ordnung. In diesem Fall erfolgt der Übergang zu Schritt 8.
Andernfalls fahren Sie mit Schritt 6 fort.
6. Die Vorzeichen der Winkelminorwerte f''(x i) werden analysiert. Wenn f''(x i) positiv definit ist, dann ist x i ein lokaler Minimalpunkt. In diesem Fall erfolgt der Übergang zu Schritt 8.
Andernfalls fahren Sie mit Schritt 7 fort.
7. Die Winkelminorwerte der Matrix -f''(x i) werden berechnet und ihre Vorzeichen analysiert.
Wenn -f''(x i) − positiv definit ist, dann ist f''(x i) negativ definit und x i ist ein lokaler Maximalpunkt.
Ansonsten ist f''(x i) undefiniert und x i ein Sattelpunkt.
8. Die Bedingung zur Bestimmung der Natur aller stationären Punkte i=N wird überprüft.
Ist diese erfüllt, sind die Berechnungen abgeschlossen.
Ist die Bedingung nicht erfüllt, wird i=i+1 angenommen und der Übergang zu Schritt 4 durchgeführt.

Beispiel Nr. 1. Bestimmen Sie die Punkte lokaler Extrema der Funktion f(x) = x 1 3 – 2x 1 x 2 + x 2 2 – 3x 1 – 2x 2

Da alle Winkelminorwerte ungleich Null sind, wird der Charakter von x 2 durch f′′(x) definiert.
Da die Matrix f''(x 2) positiv definit ist, ist x 2 ein lokaler Minimalpunkt.
Antwort: Funktion f(x) = x 1 3 – 2x 1 x 2 + x 2 2 – 3x 1 – 2x 2 hat am Punkt x = (5/3; 8/3) lokales Minimum.

$E \subset \mathbb(R)^(n)$. Sie sagen, $f$ hat lokales Maximum am Punkt $x_(0) \in E$, wenn es eine Umgebung $U$ des Punktes $x_(0)$ gibt, so dass für alle $x \in U$ die Ungleichung $f\left(x\right ) \leqslant f ist erfüllt \left(x_(0)\right)$.

Das lokale Maximum wird aufgerufen strikt , wenn die Nachbarschaft $U$ so gewählt werden kann, dass für alle $x \in U$, die von $x_(0)$ verschieden sind, $f\left(x\right)< f\left(x_{0}\right)$.

Definition
Sei $f$ echte Funktion auf der offenen Menge $E \subset \mathbb(R)^(n)$. Sie sagen, $f$ hat lokales Minimum am Punkt $x_(0) \in E$, wenn es eine Umgebung $U$ des Punktes $x_(0)$ gibt, so dass für alle $x \in U$ die Ungleichung $f\left(x\right ) \geqslant f ist erfüllt \left(x_(0)\right)$.

Ein lokales Minimum heißt strikt, wenn eine Umgebung $U$ so gewählt werden kann, dass für alle $x \in U$, die von $x_(0)$ verschieden sind, $f\left(x\right) > f\left(x_ ( 0)\right)$.

Das lokale Extremum kombiniert die Konzepte des lokalen Minimums und des lokalen Maximums.

Satz ( notwendige Bedingung Extremum der differenzierbaren Funktion)
Sei $f$ eine reelle Funktion auf der offenen Menge $E \subset \mathbb(R)^(n)$. Wenn im Punkt $x_(0) \in E$ die Funktion $f$ an diesem Punkt ein lokales Extremum hat, dann ist $$\text(d)f\left(x_(0)\right)=0.$$ Das Gleich-Null-Differential entspricht der Tatsache, dass alle gleich Null sind, d. h. $$\displaystyle\frac(\partial f)(\partial x_(i))\left(x_(0)\right)=0.$$

Im eindimensionalen Fall ist dies – . Bezeichnen wir $\phi \left(t\right) = f \left(x_(0)+th\right)$, wobei $h$ ist beliebiger Vektor. Die Funktion $\phi$ ist für Werte von $t$ definiert, die im Absolutwert hinreichend klein sind. Darüber hinaus ist es differenzierbar nach , und $(\phi)’ \left(t\right) = \text(d)f \left(x_(0)+th\right)h$.
$f$ habe ein lokales Maximum am Punkt x $0$. Das bedeutet, dass die Funktion $\phi$ bei $t = 0$ ein lokales Maximum hat und nach dem Satz von Fermat $(\phi)’ \left(0\right)=0$ ist.
Wir haben also $df \left(x_(0)\right) = 0$, d.h. Funktion $f$ am Punkt $x_(0)$ ist auf jedem Vektor $h$ gleich Null.

Definition
Punkte, an denen die Differenz Null ist, d.h. diejenigen, bei denen alle partiellen Ableitungen gleich Null sind, werden stationär genannt. Kritische Punkte Funktionen $f$ sind jene Punkte, an denen $f$ nicht differenzierbar oder gleich Null ist. Wenn der Punkt stationär ist, folgt daraus nicht, dass die Funktion an diesem Punkt ein Extremum hat.

Beispiel 1.
Sei $f \left(x,y\right)=x^(3)+y^(3)$. Dann ist $\displaystyle\frac(\partial f)(\partial x) = 3 \cdot x^(2)$,$\displaystyle\frac(\partial f)(\partial y) = 3 \cdot y^(2 )$, also ist $\left(0,0\right)$ ein stationärer Punkt, aber die Funktion hat an diesem Punkt kein Extremum. Tatsächlich ist $f \left(0,0\right) = 0$, aber es ist leicht zu erkennen, dass die Funktion in jeder Umgebung des Punktes $\left(0,0\right)$ sowohl positive als auch negative Werte annimmt.

Beispiel 2.
Die Funktion $f \left(x,y\right) = x^(2) − y^(2)$ hat einen stationären Punkt in ihrem Ursprung, aber es ist klar, dass es an diesem Punkt kein Extremum gibt.

Satz ( ausreichender Zustand Extremum).
Die Funktion $f$ sei auf der offenen Menge $E \subset \mathbb(R)^(n)$ zweimal stetig differenzierbar. Sei $x_(0) \in E$ ein stationärer Punkt und $$\displaystyle Q_(x_(0)) \left(h\right) \equiv \sum_(i=1)^n \sum_(j=1 ) ^n \frac(\partial^(2) f)(\partial x_(i) \partial x_(j)) \left(x_(0)\right)h^(i)h^(j).$ $ Dann

Wenn $Q_(x_(0))$ – , dann hat die Funktion $f$ am Punkt $x_(0)$ ein lokales Extremum, nämlich ein Minimum, wenn die Form positiv definit ist, und ein Maximum, wenn die Form positiv ist negativ definitiv;
Wenn quadratische Form$Q_(x_(0))$ ist undefiniert, dann hat die Funktion $f$ am Punkt $x_(0)$ kein Extremum.

Verwenden wir die Entwicklung nach Taylors Formel (12.7 S. 292). Wenn man bedenkt, dass die partiellen Ableitungen erster Ordnung am Punkt $x_(0)$ gleich Null sind, erhalten wir $$\displaystyle f \left(x_(0)+h\right)−f \left(x_(0)\ rechts) = \ frac(1)(2) \sum_(i=1)^n \sum_(j=1)^n \frac(\partial^(2) f)(\partial x_(i) \partial x_ (j)) \left(x_(0)+\theta h\right)h^(i)h^(j),$$ wobei $0<\theta<1$. Обозначим $\displaystyle a_{ij}=\frac{\partial^{2} f}{\partial x_{i} \partial x_{j}} \left(x_{0}\right)$. В силу теоремы Шварца (12.6 стр. 289-290) , $a_{ij}=a_{ji}$. Обозначим $$\displaystyle \alpha_{ij} \left(h\right)=\frac{\partial^{2} f}{\partial x_{i} \partial x_{j}} \left(x_{0}+\theta h\right)−\frac{\partial^{2} f}{\partial x_{i} \partial x_{j}} \left(x_{0}\right).$$ По предположению, все непрерывны и поэтому $$\lim_{h \rightarrow 0} \alpha_{ij} \left(h\right)=0. \left(1\right)$$ Получаем $$\displaystyle f \left(x_{0}+h\right)−f \left(x_{0}\right)=\frac{1}{2}\left.$$ Обозначим $$\displaystyle \epsilon \left(h\right)=\frac{1}{|h|^{2}}\sum_{i=1}^n \sum_{j=1}^n \alpha_{ij} \left(h\right)h_{i}h_{j}.$$ Тогда $$|\epsilon \left(h\right)| \leq \sum_{i=1}^n \sum_{j=1}^n |\alpha_{ij} \left(h\right)|$$ и, в силу соотношения $\left(1\right)$, имеем $\epsilon \left(h\right) \rightarrow 0$ при $h \rightarrow 0$. Окончательно получаем $$\displaystyle f \left(x_{0}+h\right)−f \left(x_{0}\right)=\frac{1}{2}\left. \left(2\right)$$ Предположим, что $Q_{x_{0}}$ – положительноопределенная форма. Согласно лемме о положительноопределённой квадратичной форме (12.8.1 стр. 295, Лемма 1) , существует такое положительное число $\lambda$, что $Q_{x_{0}} \left(h\right) \geqslant \lambda|h|^{2}$ при любом $h$. Поэтому $$\displaystyle f \left(x_{0}+h\right)−f \left(x_{0}\right) \geq \frac{1}{2}|h|^{2} \left(λ+\epsilon \left(h\right)\right).$$ Так как $\lambda>0$ und $\epsilon \left(h\right) \rightarrow 0$ für $h \rightarrow 0$, dann rechter Teil wird für jeden Vektor $h$ mit ausreichend kleiner Länge positiv sein.
Wir sind also zu dem Schluss gekommen, dass in einer bestimmten Umgebung des Punktes $x_(0)$ die Ungleichung $f \left(x\right) >f \left(x_(0)\right)$ gilt, wenn nur $ x \neq x_ (0)$ (wir setzen $x=x_(0)+h$\right). Das bedeutet, dass die Funktion am Punkt $x_(0)$ ein striktes lokales Minimum hat und damit der erste Teil unseres Satzes bewiesen ist.
Nehmen wir nun an, dass $Q_(x_(0))$ – unbestimmte Form. Dann gibt es Vektoren $h_(1)$, $h_(2)$ mit $Q_(x_(0)) \left(h_(1)\right)=\lambda_(1)>0$, $Q_ ( x_(0)) \left(h_(2)\right)= \lambda_(2)<0$. В соотношении $\left(2\right)$ $h=th_{1}$ $t>0 $. Dann erhalten wir $$f \left(x_(0)+th_(1)\right)−f \left(x_(0)\right) = \frac(1)(2) \left[ t^(2) \ lambda_(1) + t^(2) |h_(1)|^(2) \epsilon \left(th_(1)\right) \right] = \frac(1)(2) t^(2) \ left[ \lambda_(1) + |h_(1)|^(2) \epsilon \left(th_(1)\right) \right].$$ Für hinreichend kleine $t>0$ die rechte Hand Seite ist positiv. Das bedeutet, dass die Funktion $f$ in jeder Umgebung des Punktes $x_(0)$ Werte $f \left(x\right)$ annimmt, die größer als $f \left(x_(0)\right)$ sind.
Ebenso stellen wir fest, dass die Funktion $f$ in jeder Umgebung des Punktes $x_(0)$ Werte annimmt, die kleiner als $f \left(x_(0)\right)$ sind. Dies bedeutet zusammen mit dem vorherigen, dass die Funktion $f$ am Punkt $x_(0)$ kein Extremum hat.

Lassen Sie uns überlegen besonderer Fall dieses Theorems für eine Funktion $f \left(x,y\right)$ aus zwei Variablen, die in einer bestimmten Umgebung des Punktes $\left(x_(0),y_(0)\right)$ definiert sind und einen kontinuierlichen Teil haben Ableitungen erster Ordnung in dieser Umgebung und zweiter Ordnung. Nehmen Sie an, dass $\left(x_(0),y_(0)\right)$ ein stationärer Punkt ist und bezeichnen Sie $$\displaystyle a_(11)= \frac(\partial^(2) f)(\partial x ^ (2)) \left(x_(0) ,y_(0)\right), a_(12)=\frac(\partial^(2) f)(\partial x \partial y) \left(x_( 0 ), y_(0)\right), a_(22)=\frac(\partial^(2) f)(\partial y^(2)) \left(x_(0), y_(0)\right ) .$$ Dann nimmt der vorherige Satz die folgende Form an.

Satz
Sei $\Delta=a_(11) \cdot a_(22) − a_(12)^2$. Dann:

wenn $\Delta>0$, dann hat die Funktion $f$ ein lokales Extremum am Punkt $\left(x_(0),y_(0)\right)$, nämlich ein Minimum, wenn $a_(11)> 0$ und maximal, wenn $a_(11)<0$;
wenn $\Delta<0$, то экстремума в точке $\left(x_{0},y_{0}\right)$ нет. Как и в одномерном случае, при $\Delta=0$ экстремум может быть, а может и не быть.

Beispiele für Problemlösungen

Algorithmus zum Finden des Extremums einer Funktion vieler Variablen:

Auffinden stationärer Punkte;
Finden Sie das Differential 2. Ordnung an allen stationären Punkten
Unter Verwendung der hinreichenden Bedingung für das Extremum einer Funktion vieler Variablen betrachten wir das Differential zweiter Ordnung an jedem stationären Punkt

Untersuchen Sie die Funktion für das Extremum $f \left(x,y\right) = x^(3) + 8 \cdot y^(3) + 18 \cdot x — 30 \cdot y$.
Lösung
Finden wir die partiellen Ableitungen 1. Ordnung: $$\displaystyle \frac(\partial f)(\partial x)=3 \cdot x^(2) - 6 \cdot y;$$ $$\displaystyle \frac(\partial f)(\partial y)=24 \cdot y^(2) — 6 \cdot x.$$ Lassen Sie uns das System zusammenstellen und lösen: $$\displaystyle \begin(cases)\frac(\partial f)(\partial x) = 0\\\frac(\partial f)(\partial y)= 0\end(cases) \Rightarrow \begin(cases)3 \cdot x^(2) - 6 \cdot y= 0\\24 \cdot y^(2) — 6 \cdot x = 0\end(cases) \Rightarrow \begin(cases)x^(2) — 2 \cdot y= 0\\4 \cdot y^(2) — x = 0 \end(cases)$$ Aus der 2. Gleichung drücken wir $x=4 \cdot y^(2)$ aus – setzen Sie es in die 1. Gleichung ein: $$\displaystyle \left(4 \cdot y^(2) \right )^(2)-2 \cdot y=0$$ $$16 \cdot y^(4) — 2 \cdot y = 0$$ $$8 \cdot y^(4) — y = 0$$ $ $y \left(8 \cdot y^(3) -1\right)=0$$ Als Ergebnis erhält man 2 stationäre Punkte:
1) $y=0 \Rightarrow x = 0, M_(1) = \left(0, 0\right)$;
2) $\displaystyle 8 \cdot y^(3) -1=0 \Rightarrow y^(3)=\frac(1)(8) \Rightarrow y = \frac(1)(2) \Rightarrow x=1 , M_(2) = \left(\frac(1)(2), 1\right)$
Prüfen wir, ob die hinreichende Bedingung für ein Extremum erfüllt ist:
$$\displaystyle \frac(\partial^(2) f)(\partial x^(2))=6 \cdot x; \frac(\partial^(2) f)(\partial x \partial y)=-6; \frac(\partial^(2) f)(\partial y^(2))=48 \cdot y$$
1) Für den Punkt $M_(1)= \left(0,0\right)$:
$$\displaystyle A_(1)=\frac(\partial^(2) f)(\partial x^(2)) \left(0,0\right)=0; B_(1)=\frac(\partial^(2) f)(\partial x \partial y) \left(0,0\right)=-6; C_(1)=\frac(\partial^(2) f)(\partial y^(2)) \left(0,0\right)=0;$$
$A_(1) \cdot B_(1) — C_(1)^(2) = -36<0$ , значит, в точке $M_{1}$ нет экстремума.
2) Für Punkt $M_(2)$:
$$\displaystyle A_(2)=\frac(\partial^(2) f)(\partial x^(2)) \left(1,\frac(1)(2)\right)=6; B_(2)=\frac(\partial^(2) f)(\partial x \partial y) \left(1,\frac(1)(2)\right)=-6; C_(2)=\frac(\partial^(2) f)(\partial y^(2)) \left(1,\frac(1)(2)\right)=24;$$
$A_(2) \cdot B_(2) — C_(2)^(2) = 108>0$, was bedeutet, dass es am Punkt $M_(2)$ ein Extremum gibt, und da $A_(2)> 0$, dann ist das das Minimum.
Antwort: Der Punkt $\displaystyle M_(2)\left(1,\frac(1)(2)\right)$ ist der Minimalpunkt der Funktion $f$.
Untersuchen Sie die Funktion für das Extremum $f=y^(2) + 2 \cdot x \cdot y - 4 \cdot x - 2 \cdot y - 3$.
Lösung
Suchen wir stationäre Punkte: $$\displaystyle \frac(\partial f)(\partial x)=2 \cdot y - 4;$$ $$\displaystyle \frac(\partial f)(\partial y)=2 \ cdot y + 2 \cdot x — 2.$$
Lassen Sie uns das System zusammenstellen und lösen: $$\displaystyle \begin(cases)\frac(\partial f)(\partial x)= 0\\\frac(\partial f)(\partial y)= 0\end(cases ) \Rightarrow \begin(cases)2 \cdot y - 4= 0\\2 \cdot y + 2 \cdot x - 2 = 0\end(cases) \Rightarrow \begin(cases) y = 2\\y + x = 1\end(cases) \Rightarrow x = -1$$
$M_(0) \left(-1, 2\right)$ ist ein stationärer Punkt.
Überprüfen wir, ob die hinreichende Bedingung für das Extremum erfüllt ist: $$\displaystyle A=\frac(\partial^(2) f)(\partial x^(2)) \left(-1,2\right)=0 ; B=\frac(\partial^(2) f)(\partial x \partial y) \left(-1,2\right)=2; C=\frac(\partial^(2) f)(\partial y^(2)) \left(-1,2\right)=2;$$
$A \cdot B — C^(2) = -4<0$ , значит, в точке $M_{0}$ нет экстремума.
Antwort: Es gibt keine Extreme.

Zeitlimit: 0

Navigation (nur Jobnummern)

0 von 4 Aufgaben abgeschlossen

Information

Nehmen Sie an diesem Quiz teil, um Ihr Wissen über das gerade gelesene Thema zu testen: Lokale Extrema von Funktionen mehrerer Variablen.

Sie haben den Test schon einmal gemacht. Sie können es nicht erneut starten.

Testladung...

Sie müssen sich anmelden oder registrieren, um mit dem Test beginnen zu können.

Sie müssen die folgenden Tests abschließen, um diesen zu starten:

Ergebnisse

Richtige Antworten: 0 von 4

Deine Zeit:

Die Zeit ist um

Sie haben 0 von 0 Punkten erreicht (0)

Ihr Ergebnis wurde in der Bestenliste aufgezeichnet

Mit Antwort
Mit Sichtmarkierung

Aufgabe 1 von 4

1 .

Anzahl der Punkte: 1

Untersuchen Sie die Funktion $f$ für Extrema: $f=e^(x+y)(x^(2)-2 \cdot y^(2))$

Rechts

Falsch

Aufgabe 2 von 4

2 .
Anzahl der Punkte: 1
Hat die Funktion $f = 4 + \sqrt((x^(2)+y^(2))^(2))$ ein Extremum?

Definition: Der Punkt x0 wird als Punkt des lokalen Maximums (oder Minimums) einer Funktion bezeichnet, wenn die Funktion in einer Umgebung des Punktes x0 den größten (oder kleinsten) Wert annimmt, d. h. Für alle x aus einer Umgebung des Punktes x0 ist die Bedingung f(x) f(x0) (oder f(x) f(x0)) erfüllt.

Punkte mit lokalem Maximum oder Minimum werden durch einen gemeinsamen Namen vereint – Punkte mit lokalem Extremum einer Funktion.

Beachten Sie, dass die Funktion an lokalen Extrempunkten ihren Maximal- oder Minimalwert nur in einem bestimmten lokalen Bereich erreicht. Es kann Fälle geben, in denen entsprechend dem Wert уmaxуmin.

Ein notwendiges Zeichen für die Existenz eines lokalen Extremums einer Funktion

Satz . Wenn eine stetige Funktion y = f(x) ein lokales Extremum am Punkt x0 hat, dann ist die erste Ableitung an diesem Punkt entweder Null oder existiert nicht, d.h. An kritischen Punkten erster Art tritt ein lokales Extremum auf.

An lokalen Extrempunkten verläuft die Tangente entweder parallel zur 0x-Achse oder es gibt zwei Tangenten (siehe Abbildung). Beachten Sie, dass kritische Punkte eine notwendige, aber keine hinreichende Bedingung für ein lokales Extremum sind. Ein lokales Extremum tritt nur an kritischen Punkten der ersten Art auf, aber nicht an allen kritischen Punkten tritt ein lokales Extremum auf.

Zum Beispiel: Eine kubische Parabel y = x3 hat einen kritischen Punkt x0 = 0, an dem die Ableitung erfolgt y/(0)=0, aber der kritische Punkt x0=0 ist kein Extrempunkt, sondern ein Wendepunkt an ihm (siehe unten).

Ein ausreichendes Zeichen für die Existenz eines lokalen Extremums einer Funktion

Satz . Wenn das Argument einen kritischen Punkt erster Art von links nach rechts durchläuft, ist die erste Ableitung y / (x)

Ändert das Vorzeichen von „+“ zu „-“, dann hat die stetige Funktion y(x) an diesem kritischen Punkt ein lokales Maximum;

Ändert sich das Vorzeichen von „-“ zu „+“, dann hat die stetige Funktion y(x) an diesem kritischen Punkt ein lokales Minimum

ändert das Vorzeichen nicht, dann gibt es an diesem kritischen Punkt kein lokales Extremum, es gibt hier einen Wendepunkt.

Für ein lokales Maximum wird der Bereich steigender Funktion (y/0) durch den Bereich fallender Funktion (y/0) ersetzt. Für ein lokales Minimum wird der Bereich der abnehmenden Funktion (y/0) durch den Bereich der zunehmenden Funktion (y/0) ersetzt.

Beispiel: Untersuchen Sie die Funktion y = x3 + 9x2 + 15x - 9 auf Monotonie und Extremum und erstellen Sie einen Graphen der Funktion.

Finden wir kritische Punkte erster Art, indem wir die Ableitung (y/) definieren und sie mit Null gleichsetzen: y/ = 3x2 + 18x + 15 = 3(x2 + 6x + 5) = 0

Lösen wir das quadratische Trinom mithilfe der Diskriminante:

x2 + 6x + 5 = 0 (a=1, b=6, c=5) D=, x1k = -5, x2k = -1.

2) Wir unterteilen die Zahlenachse in 3 Bereiche mit kritischen Punkten und bestimmen darin die Vorzeichen der Ableitung (y/). Mithilfe dieser Vorzeichen finden wir Bereiche monotoner (steigender und fallender) Funktionen und bestimmen durch Ändern der Vorzeichen die Punkte lokaler Extremwerte (Maximum und Minimum).

Wir stellen die Forschungsergebnisse in tabellarischer Form dar, aus der sich folgende Schlussfolgerungen ziehen lassen:

1. Auf dem Intervall y /(-10) 0 steigt die Funktion monoton an (das Vorzeichen der Ableitung y wurde anhand des in diesem Intervall aufgenommenen Kontrollpunkts x = -10 geschätzt);
2. Auf dem Intervall (-5 ; -1) y /(-2) 0 nimmt die Funktion monoton ab (das Vorzeichen der Ableitung y wurde unter Verwendung des Kontrollpunkts x = -2 geschätzt, der in diesem Intervall aufgenommen wurde);
3. Im Intervall y /(0) 0 steigt die Funktion monoton an (das Vorzeichen der Ableitung y wurde anhand des in diesem Intervall aufgenommenen Kontrollpunkts x = 0 geschätzt);
4. Beim Durchlaufen des kritischen Punktes x1k = -5 ändert die Ableitung das Vorzeichen von „+“ nach „-“, daher ist dieser Punkt ein lokaler Maximalpunkt
(ymax(-5) = (-5)3+9(-5)2 +15(-5)-9=-125 + 225 - 75 - 9 =16);
5. Beim Durchlaufen des kritischen Punktes x2k = -1 ändert die Ableitung das Vorzeichen von „-“ nach „+“, daher ist dieser Punkt ein lokaler Minimalpunkt
(ymin(-1) = -1 + 9 - 15 - 9 = - 16).

x -5 (-5 ; -1) -1

3) Wir erstellen ein Diagramm basierend auf den Ergebnissen der Studie unter Verwendung zusätzlicher Berechnungen von Funktionswerten an Kontrollpunkten:

Konstruieren Sie ein rechteckiges Koordinatensystem Oxy;

Wir zeigen anhand der Koordinaten die Punkte des Maximums (-5; 16) und des Minimums (-1;-16);

Um die Grafik zu verdeutlichen, berechnen wir den Wert der Funktion an Kontrollpunkten, indem wir sie links und rechts von den Maximal- und Minimalpunkten und innerhalb des Durchschnittsintervalls auswählen, zum Beispiel: y(-6)=(-6)3 + 9(-6)2+15(-6)-9=9; y(-3)=(-3)3+9(-3)2+15(-3)-9=0;

y(0)= -9 (-6;9); (-3;0) und (0;-9) – berechnete Kontrollpunkte, die wir zeichnen, um das Diagramm zu erstellen;

Wir zeigen den Graphen in Form einer Kurve, die am Maximalpunkt nach oben und am Minimalpunkt konvex nach unten verläuft und durch die berechneten Kontrollpunkte verläuft.

Die Funktion soll am internen Punkt liegen
Region D lokales Maximum(Minimum), wenn es eine solche Umgebung des Punktes gibt
, für jeden Punkt
welches die Ungleichung enthält

Wenn eine Funktion an einem Punkt hat
lokales Maximum oder lokales Minimum, dann sagen wir, dass es an diesem Punkt ist lokales Extremum(oder einfach ein Extrem).

Satz (notwendige Voraussetzung für die Existenz eines Extremums). Wenn die differenzierbare Funktion an diesem Punkt ein Extremum erreicht
, dann jede partielle Ableitung erster Ordnung der Funktion an diesem Punkt wird es Null.

Die Punkte, an denen alle partiellen Ableitungen erster Ordnung verschwinden, werden aufgerufen stationäre Punkte der Funktion
. Die Koordinaten dieser Punkte können durch Lösen des Systems von ermittelt werden Gleichungen

Die notwendige Bedingung für die Existenz eines Extremums bei einer differenzierbaren Funktion lässt sich kurz wie folgt formulieren:

Es gibt Fälle, in denen an einzelnen Punkten einige partielle Ableitungen unendliche Werte haben oder nicht existieren (während der Rest gleich Null ist). Solche Punkte werden aufgerufen kritische Punkte der Funktion. Diese Punkte sollten ebenso wie stationäre Punkte als „verdächtig“ für ein Extremum angesehen werden.

Bei einer Funktion zweier Variablen hat die notwendige Bedingung für das Extremum, nämlich die Gleichheit der partiellen Ableitungen (Differential) im Extremumpunkt, eine geometrische Interpretation: Tangentenebene zur Oberfläche
am Extrempunkt muss parallel zur Ebene sein
.

20. Ausreichende Bedingungen für die Existenz eines Extremums

Die Erfüllung der notwendigen Bedingung für die Existenz eines Extremums zu einem bestimmten Zeitpunkt garantiert keineswegs das Vorhandensein eines Extremums dort. Als Beispiel können wir die überall differenzierbare Funktion nehmen
. Sowohl ihre partiellen Ableitungen als auch die Funktion selbst verschwinden an diesem Punkt
. In jeder Umgebung dieses Punktes gibt es jedoch beide positiven (großen).
) und negativ (kleiner
) Werte dieser Funktion. Daher wird an diesem Punkt per Definition kein Extremum beobachtet. Daher ist es notwendig, ausreichende Bedingungen zu kennen, unter denen ein Punkt, bei dem man vermutet, dass er ein Extremum ist, ein Extremumpunkt der untersuchten Funktion ist.

Betrachten wir den Fall einer Funktion zweier Variablen. Nehmen wir an, dass die Funktion
definiert, stetig und hat stetige partielle Ableitungen bis einschließlich zweiter Ordnung in der Umgebung eines Punktes
, der der stationäre Punkt der Funktion ist
, das heißt, erfüllt die Bedingungen

,
.

Führen wir die folgende Notation ein:

Satz (hinreichende Bedingungen für die Existenz eines Extremums). Lassen Sie die Funktion
erfüllt die oben genannten Bedingungen, nämlich: Es ist in einer Umgebung eines stationären Punktes differenzierbar
und ist im Punkt selbst zweimal differenzierbar
. Dann wenn

Wenn
dann die Funktion
am Punkt
erreicht

lokales Maximum bei
Und

lokales Minimum bei
.

Im Allgemeinen für die Funktion
ausreichende Bedingung für die Existenz an diesem Punkt
lokalMinimum(maximal) Ist positiv(Negativ) Gewissheit des zweiten Differentials.

Mit anderen Worten: Die folgende Aussage ist wahr.

Satz . Wenn an der Stelle
für Funktion

für alle, die gleichzeitig ungleich Null sind
, dann hat die Funktion an diesem Punkt Minimum(ähnlich zu maximal, Wenn
).

Beispiel 18.Finden Sie lokale Extrempunkte einer Funktion

Lösung. Finden wir die partiellen Ableitungen der Funktion und setzen sie mit Null gleich:

Wenn wir dieses System lösen, finden wir zwei mögliche Extrempunkte:

Finden wir die partiellen Ableitungen zweiter Ordnung für diese Funktion:

Am ersten stationären Punkt also und
Daher sind an dieser Stelle weitere Untersuchungen erforderlich. Funktionswert
an dieser Stelle ist Null:
Weiter,

bei

A

bei

Daher in jeder Umgebung des Punktes
Funktion
nimmt Werte so groß an
, und kleiner
, und daher an der Stelle
Funktion
hat per Definition kein lokales Extremum.