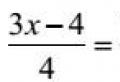Четни и нечетни функции. Как да определим четни и нечетни функции Уравнения, които дават графики на четни функции

- ; четна функция се извиква, когато за всеки две различни стойности на нейния аргумент f (x) =f(x) , например y= |x|; странно - такава функция, когато f (x) \u003d - f (x), например, y \u003d x2n + 1, където n ... ... Икономически и математически речник

четни и нечетни функции- Четна функция се извиква, когато за всеки две различни стойности на нейния аргумент f (x) =f(x) , например y= |x|; такава функция е нечетна, когато f(x) = f(x), например y= x2n+1, където n е всяко естествено число. Функции, които не са нито... Наръчник за технически преводач

ПАРИТЕТ- квантово число, което характеризира симетрията на вълновата функция на физическа система или елементарна частица при някои дискретни трансформации: ако при такава трансформация? не променя знака, тогава паритетът е положителен, ако се промени, тогава паритетът ... ... Голям енциклопедичен речник

ПАРИТЕТ НА НИВОТО- паритет на състоянието на физ. система (четност на вълните. функции), съответстващи на дадено енергийно ниво. Такова характеризиране на нива е възможно за система h c, между които ел. магн. или отрова. сили, запазващи паритета. Като се има предвид слабото взаимодействие ... ... Физическа енциклопедия

Паритет

Паритет (математика)- Четността в теорията на числата е способността на цяло число да бъде разделено без остатък на 2. Четността на функция в математическия анализ определя дали функцията променя знака, когато знакът на аргумента се променя: за четна / нечетна функция. Паритет в квантовата механика ... ... Wikipedia

ТРИГОНОМЕТРИЧНИ ФУНКЦИИ- клас елементарни функции: синус, косинус, тангенс, котангенс, секанс, косеканс. Означени съответно: sin x, cos x, tg x, ctg x, sec x, cosec x. Тригонометрични функции на реален аргумент. Нека A е точка от окръжност с център ... ... Математическа енциклопедия

ВЪТРЕШЕН ПАРИТЕТ- (P), една от характеристиките на (квантови числа) елементи. tsy, което определя поведението на неговата вълнова функция y по време на пространствена инверсия (огледално отражение), т.е., когато се променят координатите x® x, y® y, z® z. Ако с такова отражение y не променя знака, V. h. h tsy ... ... Физическа енциклопедия

Паритет на заряда- Конюгирането на заряда е операция за заместване на частица с античастица (например електрон с позитрон). Паритет на заряд Паритет на заряд е квантово число, което определя поведението на вълновата функция на частица по време на операцията по заместване на частица с античастица ... ... Wikipedia

Циклична проверка на паритета- Алгоритъмът за изчисляване на контролната сума (англ. Cyclic redundancy code, CRC cyclic redundancy code) е метод за цифрово идентифициране на определена последователност от данни, който се състои в изчисляване на контролната стойност на нейния цикличен ... ... Wikipedia

Назад напред

внимание! Визуализацията на слайда е само за информационни цели и може да не представя пълния обем на презентацията. Ако се интересувате от тази работа, моля, изтеглете пълната версия.

Цели:

• да формира концепцията за четни и нечетни функции, да научи способността да определя и използва тези свойства при изучаването на функции, чертане;
• да развива творческата активност на учениците, логическото мислене, способността за сравняване, обобщаване;
• да се култивира усърдие, математическа култура; развийте комуникативни умения .

Оборудване:мултимедийна инсталация, интерактивна дъска, раздавателни материали.

Форми на работа:фронтална и групова с елементи на търсеща и изследователска дейност.

Източници на информация:

1. Алгебра клас 9 А. Г. Мордкович. Учебник.
2. Алгебра 9 клас А. Г. Мордкович. Задачна книга.
3. Алгебра 9 клас. Задачи за обучение и развитие на учениците. Беленкова Е.Ю. Лебединцева Е.А.

ПО ВРЕМЕ НА ЗАНЯТИЯТА

1. Организационен момент

Поставяне на цели и задачи на урока.

2. Проверка на домашните

№ 10.17 (Проблемна книга 9 клас А.Г. Мордкович).

а) при = f(х), f(х) =

б) f (–2) = –3; f (0) = –1; f(5) = 69;

в) 1. D( f) = [– 2; + ∞)
2. E( f) = [– 3; + ∞)
3. f(х) = 0 за х ~ 0,4
4. f(х) >0 при х > 0,4 ; f(х) < 0 при – 2 < х < 0,4.
5. Функцията се увеличава с х € [– 2; + ∞)
6. Функцията е ограничена отдолу.
7. принаем = - 3, принаиб не съществува
8. Функцията е непрекъсната.

(Използвахте ли алгоритъма за изследване на функции?) Пързалка.

2. Нека проверим таблицата, която ви беше зададена на слайда.

Попълнете таблицата
	Домейн	Функционални нули	Интервали на постоянство		Координати на точките на пресичане на графиката с Oy
		x = -5, х = 2	х € (–5;3) U U(2;∞)	х € (–∞;–5) U U (–3;2)
	x ∞ -5, x ≠ 2		х € (–5;3) U U(2;∞)	х € (–∞;–5) U U (–3;2)
	x ≠ -5, x ≠ 2		x € (–∞; –5) U U(2;∞)	x € (–5; 2)

3. Актуализация на знанията

– Дадени са функции.
– Посочете домейна на дефиниция за всяка функция.
– Сравнете стойността на всяка функция за всяка двойка стойности на аргументи: 1 и – 1; 2 и - 2.
– За кои от дадените функции в областта на дефиниция са равенствата f(– х) = f(х), f(– х) = – f(х)? (поставете данните в таблицата) пързалка

		f(1) и f(– 1)	f(2) и f(– 2)	диаграми	f(– х) = –f(х)	f(– х) = f(х)
1. f(х) =
2. f(х) = х 3
3. f(х) = | х |
4.f(х) = 2х – 3
5. f(х) =	х ≠ 0
6. f(х)=	х > –1		и не е дефиниран.

4. Нов материал

- Докато вършим тази работа, момчета, разкрихме още едно свойство на функцията, непознато за вас, но не по-малко важно от останалите - това е четността и нечетността на функцията. Запишете темата на урока: „Четни и нечетни функции“, нашата задача е да се научим как да определяме четните и нечетните функции, да разберем значението на това свойство при изучаването на функциите и чертането.
И така, нека намерим определенията в учебника и прочетем (стр. 110) . пързалка

Деф. 1функция при = f (х), дефинирана върху множеството X, се нарича дори, ако за някаква стойност хЄ X в ход равенство f (–x) = f (x). Дай примери.

Деф. 2функция y = f(x), дефинирана върху множеството X се нарича странно, ако за някаква стойност хЄ X е изпълнено равенството f(–х)= –f(х). Дай примери.

Къде срещнахме термините "четно" и "нечетно"?
Коя от тези функции ще бъде четна, според вас? Защо? Кои са странни? Защо?
За всяка функция на формата при= x n, Където не цяло число, може да се твърди, че функцията е нечетна за не нечетно и функцията е четно за н- дори.
– Преглед на функции при= и при = 2х– 3 не е нито четно, нито нечетно, т.к равенствата не са спазени f(– х) = – f(х), f(– х) = f(х)

Изследването на въпроса дали една функция е четна или нечетна се нарича изследване на функция за паритет.пързалка

Дефиниции 1 и 2 се занимават със стойностите на функцията при x и - x, като по този начин се приема, че функцията също е дефинирана при стойността х, и при - х.

ОПР 3.Ако числово множество заедно с всеки от неговите елементи x съдържа противоположния елемент x, тогава множеството хсе нарича симетрично множество.

Примери:

(–2;2), [–5;5]; (∞;∞) са симетрични множества, а , [–5;4] са несиметрични.

- Четните функции имат ли област на дефиниция - симетрично множество? Странните?
- Ако D( f) е асиметрично множество, тогава каква е функцията?
– По този начин, ако функцията при = f(х) е четен или нечетен, тогава неговият домейн на дефиниция е D( f) е симетрично множество. Но вярно ли е обратното, ако областта на дадена функция е симетрично множество, тогава тя е четна или нечетна?
- Така че наличието на симетрично множество от областта на дефиниране е необходимо условие, но не и достатъчно.
– И така, как можем да изследваме функцията за паритет? Нека се опитаме да напишем алгоритъм.

пързалка

Алгоритъм за изследване на функция за паритет

1. Определете дали областта на функцията е симетрична. Ако не, тогава функцията не е нито четна, нито нечетна. Ако да, тогава преминете към стъпка 2 от алгоритъма.

2. Напишете израз за f(–х).

3. Сравнете f(–х).И f(х):

• Ако f(–х).= f(х), тогава функцията е четна;
• Ако f(–х).= – f(х), тогава функцията е нечетна;
• Ако f(–х) ≠ f(х) И f(–х) ≠ –f(х), тогава функцията не е нито четна, нито нечетна.

Примери:

Изследвайте функцията за паритет а) при= x 5 +; б) при= ; V) при= .

Решение.

а) h (x) \u003d x 5 +,

1) D(h) = (–∞; 0) U (0; +∞), симетрично множество.

2) h (- x) \u003d (-x) 5 + - x5 - \u003d - (x 5 +),

3) h (- x) \u003d - h (x) \u003d\u003e функция h(x)= x 5 + странно.

б) y =,

при = f(х), D(f) = (–∞; –9)? (–9; +∞), асиметрично множество, така че функцията не е нито четна, нито нечетна.

V) f(х) = , y = f(x),

1) D( f) = (–∞; 3] ≠ ; b) (∞; –2), (–4; 4]?

Вариант 2

1. Даденото множество симетрично ли е: а) [–2;2]; b) (∞; 0], (0; 7) ?

А); б) y \u003d x (5 - x 2). 2. Проверете функцията за паритет:

а) y \u003d x 2 (2x - x 3), b) y \u003d

3. На фиг. начертан при = f(х), за всички х, отговарящи на условието х? 0.
Начертайте функцията при = f(х), Ако при = f(х) е четна функция.

3. На фиг. начертан при = f(х), за всички x, удовлетворяващи x? 0.
Начертайте функцията при = f(х), Ако при = f(х) е странна функция.

Взаимна проверка включена пързалка.

6. Домашна работа: №11.11, 11.21,11.22;

Доказателство за геометричния смисъл на свойството паритет.

*** (Присвояване на опцията USE).

1. Нечетната функция y \u003d f (x) е дефинирана на цялата реална линия. За всяка неотрицателна стойност на променливата x стойността на тази функция съвпада със стойността на функцията g( х) = х(х + 1)(х + 3)(х– 7). Намерете стойността на функцията h( х) = при х = 3.

7. Обобщаване

Зависимостта на променливата y от променливата x, при която всяка стойност на x съответства на една единствена стойност на y, се нарича функция. Нотацията е y=f(x). Всяка функция има редица основни свойства, като монотонност, паритет, периодичност и други.

Разгледайте свойството паритет по-подробно.

Функция y=f(x) се извиква дори ако отговаря на следните две условия:

2. Стойността на функцията в точката x, принадлежаща на обхвата на функцията, трябва да бъде равна на стойността на функцията в точката -x. Тоест, за всяка точка x, от домейна на функцията, трябва да е вярно следното равенство f (x) \u003d f (-x).

Графика на четна функция

Ако построите графика на четна функция, тя ще бъде симетрична спрямо оста y.

Например функцията y=x^2 е четна. Нека го проверим. Областта на дефиниране е цялата числена ос, което означава, че тя е симетрична спрямо точката O.

Вземете произволно x=3. f(x)=3^2=9.

f(-x)=(-3)^2=9. Следователно f(x) = f(-x). Така и двете условия за нас са изпълнени, което означава, че функцията е четна. По-долу има графика на функцията y=x^2.

Фигурата показва, че графиката е симетрична спрямо оста y.

Графика на нечетна функция

Функция y=f(x) се нарича нечетна, ако удовлетворява следните две условия:

1. Домейнът на дадената функция трябва да бъде симетричен спрямо точката O. Тоест, ако някаква точка a принадлежи на домейна на функцията, тогава съответната точка -a също трябва да принадлежи на домейна на дадената функция.

2. За всяка точка x, от областта на функцията, трябва да бъде изпълнено следното равенство f (x) \u003d -f (x).

Графиката на нечетна функция е симетрична спрямо точката O - началото. Например функцията y=x^3 е нечетна. Нека го проверим. Областта на дефиниране е цялата числена ос, което означава, че тя е симетрична спрямо точката O.

Вземете произволно x=2. f(x)=2^3=8.

f(-x)=(-2)^3=-8. Следователно f(x) = -f(x). Така и двете условия за нас са изпълнени, което означава, че функцията е нечетна. По-долу има графика на функцията y=x^3.

Фигурата ясно показва, че нечетната функция y=x^3 е симетрична по отношение на началото.

Скриване на шоуто

Начини за задаване на функция

Нека функцията е дадена по формулата: y=2x^(2)-3 . Като присвоите произволна стойност на независимата променлива x, можете да използвате тази формула, за да изчислите съответните стойности на зависимата променлива y. Например, ако x=-0,5 , тогава използвайки формулата, получаваме, че съответната стойност на y е y=2 \cdot (-0,5)^(2)-3=-2,5 .

Като се има предвид всяка стойност, взета от аргумента x във формулата y=2x^(2)-3 , може да се изчисли само една функционална стойност, която съответства на нея. Функцията може да бъде представена като таблица:

х	−2	−1	0	1	2	3
г	−4	−3	−2	−1	0	1

Използвайки тази таблица, можете да разберете, че за стойността на аргумента -1 ще съответства стойността на функцията -3; и стойността x=2 ще съответства на y=0 и т.н. Също така е важно да знаете, че всяка стойност на аргумент в таблицата отговаря само на една стойност на функцията.

Повече функции могат да бъдат зададени с помощта на графики. С помощта на графиката се установява коя стойност на функцията корелира с определена стойност на x. Най-често това ще бъде приблизителна стойност на функцията.

Четна и нечетна функция

Функцията е дори функция, когато f(-x)=f(x) за всяко x от домейна. Такава функция ще бъде симетрична спрямо оста Oy.

Функцията е странна функциякогато f(-x)=-f(x) за всяко x в домейна. Такава функция ще бъде симетрична спрямо началото O (0;0) .

Функцията е дори не, нито страннои се обади обща функциякогато няма симетрия спрямо оста или началото.

Разглеждаме следната функция за паритет:

f(x)=3x^(3)-7x^(7)

D(f)=(-\infty ; +\infty) със симетрична област на дефиниция относно произхода. f(-x)= 3 \cdot (-x)^(3)-7 \cdot (-x)^(7)= -3x^(3)+7x^(7)= -(3x^(3)-7x^(7))= -f(x).

Следователно функцията f(x)=3x^(3)-7x^(7) е нечетна.

Периодична функция

Функцията y=f(x), в чиято област f(x+T)=f(x-T)=f(x) е вярна за всяко x, се нарича периодична функцияс период T \neq 0 .

Повторение на графиката на функцията върху всеки сегмент от абсцисната ос, който има дължина T .

Интервали, където функцията е положителна, т.е. f (x) > 0 - сегменти от абсцисната ос, които съответстват на точките от графиката на функцията, които лежат над абсцисната ос.

f(x) > 0 включено (x_(1); x_(2)) \чаша (x_(3); +\infty)

Пропуски, при които функцията е отрицателна, т.е. f(x)< 0 - отрезки оси абсцисс, которые отвечают точкам графика функции, лежащих ниже оси абсцисс.

f(x)< 0 на (-\infty; x_(1)) \чаша (x_(2); x_(3))

Ограничение на функцията

ограничен отдолуобичайно е да се извиква функция y=f(x), x \in X, когато съществува число A, за което неравенството f(x) \geq A е валидно за всяко x \in X .

Пример за функция, ограничена по-долу: y=\sqrt(1+x^(2)), тъй като y=\sqrt(1+x^(2)) \geq 1 за всяко x .

ограничен отгорефункция y=f(x), x \in X се извиква, ако съществува число B, за което неравенството f(x) \neq B е в сила за всяко x \in X .

Пример за функция, ограничена по-долу: y=\sqrt(1-x^(2)), x \in [-1;1]тъй като y=\sqrt(1+x^(2)) \neq 1 за всяко x \in [-1;1] .

Ограниченобичайно е да се извиква функция y=f(x), x \in X, когато съществува число K > 0, за което неравенството \left | f(x) \right | \neq K за всяко x \in X .

Пример за ограничена функция: y=\sin x е ограничена на цялата числова ос, защото \ляво | \sin x \right | \neq 1.

Нарастваща и намаляваща функция

Прието е да се говори за функция, която нараства на разглеждания интервал като увеличаваща се функциякогато по-голяма стойност на x ще съответства на по-голяма стойност на функцията y=f(x) . От тук се оказва, че като вземем от разглеждания интервал две произволни стойности на аргумента x_(1) и x_(2) , и x_(1) > x_(2) , ще бъде y(x_(1)) > y(x_(2)) .

Извиква се функция, която намалява на разглеждания интервал намаляваща функциякогато по-голяма стойност на x ще съответства на по-малка стойност на функцията y(x) . От тук се оказва, че като вземем от разглеждания интервал две произволни стойности на аргумента x_(1) и x_(2) , и x_(1) > x_(2) , ще бъде y(x_(1))< y(x_{2}) .

Функционални корениобичайно е да се назовават точките, в които функцията F=y(x) пресича абсцисната ос (те се получават в резултат на решаване на уравнението y(x)=0 ).

а) Ако четна функция расте при x > 0, тогава тя намалява при x< 0

б) Когато четна функция намалява за x > 0, тогава тя нараства за x< 0

в) Когато нечетна функция расте за x > 0, тогава тя също нараства за x< 0

г) Когато нечетна функция намалява за x > 0, тогава тя също ще намалява за x< 0

Функционални крайности

Функционална минимална точка y=f(x) е обичайно да наричаме такава точка x=x_(0) , в която нейната околност ще има други точки (с изключение на точката x=x_(0) ), и тогава за тях ще бъде изпълнено неравенството f(x) > f(x_(0)). y_(min) - обозначение на функцията в точката min.

Функционална максимална точка y=f(x) е обичайно да наричаме такава точка x=x_(0) , в която нейната околност ще има други точки (с изключение на точката x=x_(0) ), и тогава за тях ще бъде изпълнено неравенството f(x)< f(x^{0}) . y_{max} - обозначение функции в точке max.

Необходимо условие

Според теоремата на Ферма: f"(x)=0, тогава когато функцията f(x) , която е диференцируема в точката x_(0) , в тази точка ще се появи екстремум.

Достатъчно условие

1. Когато знакът на производната се промени от плюс на минус, тогава x_(0) ще бъде минималната точка;
2. x_(0) - ще бъде максимална точка само когато производната промени знака от минус на плюс при преминаване през стационарната точка x_(0) .

Най-голямата и най-малката стойност на функцията на интервала

Стъпки на изчисление:

1. Търси се производна f"(x) ;
2. Намират се стационарни и критични точки на функцията и се избират принадлежащите към интервала;
3. Стойностите на функцията f(x) се намират в стационарните и критичните точки и краищата на сегмента. Най-малкият от резултатите ще бъде най-малката стойност на функцията, и още - най велик.

. За да направите това, използвайте милиметрова хартия или графичен калкулатор. Изберете произволен брой числови стойности за независимата променлива x (\displaystyle x)и ги включете във функцията за изчисляване на стойностите на зависимата променлива y (\displaystyle y). Поставете намерените координати на точките в координатната равнина и след това свържете тези точки, за да изградите графика на функцията.

• Заменете положителните числови стойности във функцията x (\displaystyle x)и съответните отрицателни числови стойности. Например, дадена функция f (x) = 2 x 2 + 1 (\displaystyle f(x)=2x^(2)+1). Заменете следните стойности в него x (\displaystyle x):

Проверете дали графиката на функцията е симетрична спрямо оста y.Симетрията се отнася до огледалния образ на графиката спрямо оста y. Ако частта от графиката отдясно на оста y (положителни стойности на независимата променлива) съвпада с частта от графиката отляво на оста y (отрицателни стойности на независимата променлива), графиката е симетрична спрямо оста y. Ако функцията е симетрична спрямо оста y, функцията е четна.

Проверете дали графиката на функцията е симетрична спрямо началото.Началото е точката с координати (0,0). Симетрия относно произхода означава, че положителна стойност y (\displaystyle y)(с положителна стойност x (\displaystyle x)) съответства на отрицателна стойност y (\displaystyle y)(с отрицателна стойност x (\displaystyle x)), и обратно. Нечетните функции имат симетрия по отношение на произхода.

Проверете дали графиката на функцията има някаква симетрия.Последният тип функция е функция, чиято графика няма симетрия, т.е. няма огледален образ както спрямо оста y, така и спрямо началото. Например, дадена функция.

• Заменете няколко положителни и съответните отрицателни стойности във функцията x (\displaystyle x):
• Според получените резултати няма симетрия. Стойности y (\displaystyle y)за противоположни стойности x (\displaystyle x)не съвпадат и не са противоположни. Следователно функцията не е нито четна, нито нечетна.
• Моля, имайте предвид, че функцията f (x) = x 2 + 2 x + 1 (\displaystyle f(x)=x^(2)+2x+1)може да се напише така: f (x) = (x + 1) 2 (\displaystyle f(x)=(x+1)^(2)). Записана в тази форма, функцията изглежда четна, защото има четен показател. Но този пример доказва, че формата на функция не може да бъде бързо определена, ако независимата променлива е оградена в скоби. В този случай трябва да отворите скобите и да анализирате получените показатели.