مکان هندسی نقاط قضیه ای در مورد مکان نقاطی که از دو نقطه داده شده فاصله مساوی دارند، به اشکال هندسی و تحلیلی. بیایید روش حل این مشکل را سیستماتیک کنیم
مکان هندسی نقاط عمود بر میانه. نیمساز زاویه.
دایره. دایره . مرکز دایره شعاع. قوس سکنت. آکورد.
قطر. مماس و خواص آن بخش. بخش. زوایا در یک دایره.
طول کمان . رادیان. روابط بین عناصر یک دایره.
مکان هندسی – این یک مجموعه است هر کسامتیاز، رضایت بخش معین داده شدهشرایط
مثال 1. میانه عمود هر قطعه یک هندسی است
مکان نقاط (یعنی مجموعه همه نقاط)، فاصله یکسان از جانب
انتهای این بخش اجازه دهید PO AB و AO = OB:

سپس، فواصل از هر نقطهپ ، روی عمود بر میانه خوابیده است PO، تا انتهای A و B بخش AB یکسان و مساوید
بدین ترتیب، هر نقطه از عمود بر میانه بخشدارد دارایی زیر: از انتهای بخش به یک اندازه فاصله دارد.
مثال 2. نیمساز زاویه وجود دارد مکان نقاطی که از دو طرف آن فاصله دارند .
مثال 3 . دایره محل نقاط است (یعنی تعداد زیادی کیفیت
تمام نکات) مساوی فاصله از مرکز آن (در شکل خدا حافظ زانا به تنهایی
از این نقاط - A).

دایره - این مکان نقاط (یعنی مجموعه تمام نقاط) روی صفحه ,مساوی فاصله از یک نقطهمرکز دایره نامیده می شود. پاره ای که مرکز یک دایره را به هر نقطه روی آن متصل می کند نامیده می شود شعاعو تعیین شده استrیا آر. قسمتی از صفحه که به یک دایره محدود می شود نامیده می شود اطراف. بخشی از یک دایره (
آ مترب شکل 39) تماس گرفت قوس سر راست پی کیوعبور از نقاط م و ن دایره ها (شکل 39 ) نامیده شد جدا کردنو بخش آن MN ، در داخل دایره دراز کشیده - وتر
آکوردی که از مرکز دایره می گذرد (به عنوان مثال،
قبل از میلاد مسیح. ، شکل 39)، نامیده می شودقطرو تعیین شده است دیا D.قطر بزرگترین وتر برابر با دو شعاع (د= 2 r).
مماس. فرض کنید سکنتپی کیو (شکل 40) از نقاط عبور می کندک و م حلقه ها بگذارید این نکته را نیز فرض کنیمم در امتداد یک دایره حرکت می کند و به یک نقطه نزدیک می شود K. سپس سکنت PQ با چرخش حول نقطه، موقعیت خود را تغییر خواهد دادک . با نزدیک شدن به موضوع M به نقطه K قطع PQ به یک موقعیت محدود کننده AB تمایل دارد. سر راست AB تماس گرفت مماس به دایره در یک نقطه K. نقطه K تماس گرفت نقطه تماس. مماس و دایره فقط یک نقطه مشترک دارند - نقطه تماس.
خواص مماس.
1) بهمماس بر دایره عمود بر شعاع رسم شده است به نقطه تماس(AB OK، شکل 40) .
2) از نقطه ای خارج از دایره، دو مماس را می توان به آن رسم کرد
همان دایره؛ بخش های آنها برابر است (شکل 41).
بخش - این بخشی از یک دایره است، محدود به یک قوس ACB و آکورد مربوطه AB (شکل 42). طول عمود برسی دی از وسط آکورد کشیده شده است AB تا زمانی که با قوس تقاطع پیدا کند ACB ، تماس گرفت ارتفاعبخش.
بخش – بخشی از یک دایره است که توسط یک کمان محدود شده استآ مترب و دو شعاع OA و OB، به انتهای این قوس کشیده شده است (شکل 43).

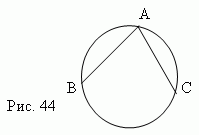
زوایا در یک دایره. زاویه مرکزی – زاویه تشکیل شده توسط دو شعاع ( A.O.B. شکل 43). زاویه حکاکی شده- زاویه ای که توسط دو آکورد تشکیل شده است AB و AC ، از یکی آنها انجام می شود نقطه مشترک ( BA C، شکل 44). زاویه محصور شده- زاویه تشکیل شده توسط دو مماس AB و AC برگرفته از یک نقطه مشترک ( BAC، شکل 41).
طول کمان یک دایره متناسب با شعاع آن استr و زاویه مرکزی مربوطه :
l = r
بنابراین، اگر طول قوس را بدانیم
لو شعاع r، سپس مقدار زاویه مرکزی مربوطه می توان با رابطه آنها تعیین کرد: = l/r.این فرمول مبنایی برای تعیین است اندازه گیری رادیانگوشه ها بنابراین، اگرل = rکه = 1 و می گوییم که زاویه برابر با 1 رادیان (این را با: = 1 خوشحالم). بنابراین ما داریم تعریف زیررادیان به عنوان واحد اندازه گیری زوایا: رادیان است زاویه مرکزی ( AOB، شکل 43)، که طول قوس آن برابر با شعاع آن است (آ متر B = AO، شکل 43). بنابراین، اندازه گیری رادیان هر زاویه، نسبت طول قوس کشیده شده است شعاع دلخواهو بین اضلاع این زاویه به شعاع آن محصور شده است.به طور خاص، با توجه به فرمول طول قوس، محیطسیرا می توان به صورت زیر بیان کرد:
جایی که به عنوان نسبت تعریف شده استسیبه قطر دایره 2r :
= ج/ 2 r
عدد گنگ; مقدار تقریبی آن 3.1415926…
از طرف دیگر، 2- این زاویه دایره ایدایره ای که در سیستم درجه اندازه گیری برابر با 360 درجه است. در عمل اغلب اتفاق می افتد که هم شعاع قوس و هم زاویه ناشناخته هستند. در این مورد، طول قوس را می توان با استفاده از فرمول تقریبی هویگنس محاسبه کرد:
پ 2ل + (2ll) / 3 ,
جایی که (شکل 42 را ببینید): پ- طول قوس ACB؛ ل- طول وتر AC؛ L– طول وتر AB. اگر قوس بیشتر از 60 نباشدº ، خطای نسبی این فرمول از 0.5٪ تجاوز نمی کند.
روابط بین عناصر یک دایره. زاویه حکاکی شده (ABC، شکل 45) برابر با نصفزاویه مرکزی , تکیه بر همان قوس آ mC (AOC، شکل 45) . از همین رو، تمام زوایای حکاکی شده(شکل 45)، استراحت روی یکی و اون یکی همان قوس(آ مترسی ، شکل 45)، برابر هستند.و از آنجایی که زاویه مرکزی دارای همان تعداد درجات قوس آن است (آ مترسی ، شکل 45)، سپس هر زاویه محاطی با نصف قوسی که روی آن قرار دارد اندازه گیری می شود(در مورد ماآ مترج).

همه زوایای محاطی که یک نیم دایره را در بر می گیرند (APB، AQB، ...، شکل 46)، سر راست (ثابت کن لطفا!).
گوشه(AOD، شکل 47 )، که توسط دو آکورد تشکیل شده است( AB و CD)، معیارهای نصف مجموع کمان های محصور بین اضلاع آن است: (آ n D+C مترب) / 2 .

گوشه(AOD، شکل 48) , توسط دو بخش تشکیل شده است (AO و OD ), با نصف اختلاف قوس اندازه گیری می شود، منعقد شده بین طرفین آن: (آ n D–B مترسی ) / 2. جدا کردن(CO و BO ), با نصف اختلاف اندازه گیری می شود قوس های محصور بین دو طرف آن: (ب مترسی – سی n D ) / 2 .
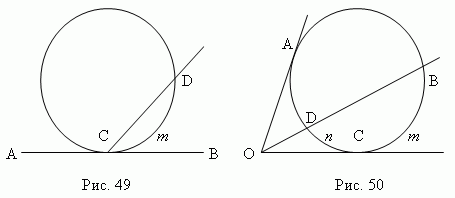
زاویه محصور شده(AOC، شکل 50 )، که توسط دو مماس تشکیل شده است( CO و AO ), با نصف اختلاف کمان های محصور شده بین آن اندازه گیری می شود مهمانی:(ABC – CDA) / 2 .
محصولات بخش های آکورد (AB و CD ، شکل 51 یا شکل 52)، که آنها بر اساس نقطه تقاطع به آنها تقسیم می شوند، برابر هستند: AO·BO = CO·DO.
مماس مربع K برابر با محصولبرش به قسمت بیرونی آن (شکل 50): OA 2 = O B O D (اثباتش کن!). این ملک را می توان به عنوان یک مورد خاص در نظر گرفتشکل 52.

آکورد(AB ، شکل 53) ، عمود بر قطر(سی دی )، در نقطه تقاطع آنها تقسیم می شود O به نصف: AO = OB.
( سعی کن ثابت کنی!).
اهداف درس:
- آموزشی: نمایش روش جدیدحل مسائل مربوط به ساخت مکان هندسی نقاط. یاد بگیرید که از آن در حل مشکلات استفاده کنید.
- آموزشی: توسعه از نظر بصری فیگوراتیوفكر كردن؛ علاقه شناختی
- آموزشی: توسعه توانایی برنامه ریزی کار، جستجو راه های منطقیاجرای آن، توانایی دفاع از عقیده خود با دلیل، و ارزیابی انتقادی نتیجه.
اهداف درس:
- مطالعه مطالب جدید
- مهارت حل مسئله دانش آموزان را آزمایش کنید.
طرح درس:
- تعاریف
- مثال 1.
- مثال 2.
- مثال 3.
- بخش تئوری
- مفاهیم کلی
معرفی.
فرهنگ مصر باستان و بابل در زمینه ریاضیات توسط یونانیان ادامه یافت. آنها نه تنها تمام تجربه هندسه خود را آموختند، بلکه بسیار فراتر رفتند. دانشمندان یونان باستانموفق به آوردن انباشته شده است دانش هندسیو بنابراین پایه های هندسه را به عنوان یک علم قیاسی پی ریزی می کند.
بازرگانان یونانی با تخمگذار با ریاضیات شرقی آشنا شدند مسیرهای تجاری. اما مردم شرق تقریباً به تئوری نمی پرداختند و یونانیان به سرعت این را کشف کردند. سؤال کردند: چرا؟ مثلث متساوی الساقیندو زاویه در پایه برابر است. چرا مساحت مثلث برابر با نصف مساحت مستطیل است؟ بر همین اساسو ارتفاعات؟
متأسفانه، هیچ منبع اولیهای برای توصیف وجود ندارد دوره اولیهتوسعه ریاضیات یونانی فقط به لطف متون مرمت شده قرن چهارم قبل از میلاد و آثار دانشمندان عرب که از نظر ترجمه آثار نویسندگان غنی بود. یونان باستان، ما نسخه هایی از اقلیدس، ارشمیدس، آپولونیوس و دیگران داریم مردم بزرگ. اما در این آثار یک علم ریاضی کاملاً توسعه یافته قبلاً ارائه شده است.
ریاضیات یونان باستان از قرن ششم قبل از میلاد، مسیر طولانی و پیچیدهای را طی کرد. و تا قرن ششم. مورخان علم سه دوره از رشد آن را مطابق با ماهیت دانش تشخیص می دهند:
- تجمع فردی حقایق ریاضیو مشکلات (6 - 5 B.B. BC).
- سیستم سازی دانش کسب شده (قرن 4 - 3 قبل از میلاد).
- دوره ریاضیات محاسباتی (قرن سوم قبل از میلاد - قرن ششم).
مکان هندسی نقاط (GLP).
تعاریف
موقعیت هندسی- اصطلاحی که در ادبیات قدیمی هندسه استفاده می شود و هنوز هم در آن استفاده می شود ادبیات آموزشی، برای نشان دادن مجموعه ای از نقاط که شرایطی را برآورده می کند، معمولا، طبیعت هندسی. به عنوان مثال: مکان نقاطی که از دو نقطه داده شده A و B فاصله دارند عمود بر عمود بربه بخش AB. گاهی اوقات در مورد مکان هندسی خطوط مستقیم و اشکال دیگر صحبت می کنند.
این نام با ایده یک خط به عنوان یک "مکان" که نقاط روی آن قرار دارند مرتبط است.
در هندسه، مسیر حرکت یک نقطه مطابق با یک فرمول یا شرایط معین. به عنوان مثال، دایره مکان نقطه ای است که در یک صفحه حرکت می کند به طوری که فاصله مکان آن تا مرکز بدون تغییر باقی می ماند.
مکان هندسی نقاط (GMT)مجموعه ای از نقاط است که شامل تمام نقاطی است که راضی کننده است شرط معینو فقط آنها
مکان هندسی نقاط (GMT)- شکل گفتاری در ریاضیات که برای تعیین استفاده می شود شکل هندسیبه عنوان مجموعه ای از نقاط که دارای خاصیت هستند.
مثال ها.
- عمود بر یک پاره، مکان نقاطی است که از انتهای آن پاره فاصله دارند.
- دایره مکان نقاطی است که از یک نقطه معین فاصله دارند که مرکز دایره نامیده می شود.
- سهمی مکان نقاطی است که از یک نقطه (به نام کانون) و یک خط (به نام جهت) فاصله دارند.
مثال 1.
میانه عمود هر پاره، مکان نقاط (یعنی مجموعه همه نقاط) است که از انتهای این قطعه فاصله دارند. بگذارید PO بر AB عمود باشد و AO = OB:
سپس، فواصل از هر نقطه P که روی میانه عمود PO قرار دارد تا انتهای A و B قطعه AB یکسان و برابر با d است.
بنابراین، هر نقطه از میانه عمود یک قطعه دارای ویژگی زیر است: فاصله آن از انتهای قطعه.
مثال 2.
نیمساز یک زاویه مکان نقاطی است که از اضلاع آن فاصله دارند.
مثال 3.
دایره مکان نقاط (یعنی مجموعه همه نقاط) است که از مرکز آن فاصله دارند (شکل یکی از این نقاط را نشان می دهد - A).
آکوردگذر از مرکز دایره (مثلاً قبل از میلاد، شکل 1) قطر نامیده می شود و به آن d یا D نشان داده می شود. قطربزرگترین وتر برابر با دو شعاع (d = 2 r) است.
مماس. فرض کنید سکنت PQ (شکل 2) از نقاط K و M دایره عبور می کند. همچنین فرض کنید که نقطه M در امتداد یک دایره حرکت می کند و به نقطه K نزدیک می شود. سپس سکانس PQ موقعیت خود را تغییر می دهد و حول نقطه K می چرخد. همانطور که نقطه M به نقطه K نزدیک می شود، PQ مقطع به یک موقعیت محدود کننده AB تمایل پیدا می کند. خط AB را مماس بر دایره در نقطه K می نامند و نقطه K را نقطه مماس می نامند. مماس و دایره فقط یک نقطه مشترک دارند - نقطه تماس.
خواص مماس.
- مماس بر دایره عمود بر شعاع رسم شده به نقطه تماس است (AB عمود بر OK است، شکل 2).
- از نقطه ای خارج از دایره، دو مماس را می توان به یک دایره رسم کرد. قطعات آنها برابر با AB=AC است (شکل 3).
بخش- این بخشی از دایره است که توسط قوس ACB و وتر مربوطه AB محدود شده است (شکل 4). طول سی دی عمود بر کشیده شده از وسط وتر AB تا محل تقاطع با قوس ACB را ارتفاع پاره می گویند.
زوایا در یک دایره.
زاویه مرکزی زاویه ای است که توسط دو شعاع تشکیل شده است (∠AOB، شکل 5). زاویه محاطی، زاویهای است که توسط دو وتر AB و AC که از نقطه مشترک آنها کشیده شدهاند تشکیل میشود (∠BAC، شکل 4). زاویه محصور، زاویه ای است که توسط دو مماس AB و AC که از یک نقطه مشترک کشیده شده اند تشکیل می شود (∠BAC، شکل 3).
روابط بین عناصر یک دایره.
زاویه حکاکی شده(∠ABC، شکل 7) برابر است با نیمی از زاویه مرکزی بر اساس همان قوس AmC (∠AOC، شکل 7). بنابراین، تمام زوایای محاط شده (شکل 7) بر اساس یک قوس (AmC، شکل 7) برابر هستند. و از آنجایی که زاویه مرکزی دارای همان تعداد درجات قوس آن است (AmC، شکل 7)، پس هر زاویه محاطی شده با نصف قوسی که روی آن قرار دارد اندازه گیری می شود (در مورد ما، AmC).
تمام زوایای محاط شده بر اساس یک نیم دایره (∠APB، ∠AQB، ...، شکل 8) زاویه قائمه هستند.
گوشه(∠AOD، شکل 9)، که توسط دو آکورد (AB و CD) تشکیل شده است، با نصف مجموع کمان های محصور بین دو طرف آن اندازه گیری می شود: (AnD + CmB) / 2.
زاویه (∠AOD، شکل 10) که توسط دو بخش (AO و OD) تشکیل شده است با نصف اختلاف کمان های محصور بین اضلاع آن اندازه گیری می شود: (AnD – BmC) / 2.
زاویه (∠DCB، شکل 11) ایجاد شده توسط مماس و وتر (AB و CD) با نصف قوس موجود در آن اندازه گیری می شود: CmD / 2.
زاویه (∠BOC، شکل 12) تشکیل شده توسط مماس و سکنت (CO و BO) با نصف اختلاف کمان بین اضلاع آن اندازه گیری می شود: (BmC – CnD) / 2.
زاویه محصور شده (∠AOC، شکل 12)، که توسط دو مماس (CO و AO) تشکیل شده است، با نصف اختلاف کمان بین اضلاع آن اندازه گیری می شود: (ABC – CDA) / 2.
محصولات بخش های آکورد (AB و CD، شکل 13 یا شکل 14)، که آنها بر اساس نقطه تقاطع به آنها تقسیم می شوند، برابر هستند: AO · BO = CO · DO.
مربع مماس برابر است با حاصل ضرب سکنت و قسمت بیرونی آن (شکل 12): OA 2 = OB · OD. این ویژگی را می توان به عنوان مورد خاصشکل 14.
آکورد(AB ، شکل 15) ، عمود بر قطر(سی دی) , Oبه نصف: AO = OB.
برنج. 15
حقیقت جالب:
تعطیلات پی را تبریک می گویم.

به بیان ساده زبان علمی، عدد "Pi" نسبت محیط دایره به قطر آن است. این یک چیز ساده به نظر می رسد، اما ذهن ریاضیدانان را با آن هیجان زده می کند زمان های قدیم. و همچنان نگران است. به حدی که دانشمندان - حدود 20 سال پیش - موافقت کردند که تعطیلات این تاریخ را جشن بگیرند. و از کل جامعه مترقی خواستند که به جشن ها بپیوندند. او به آن ملحق می شود: او Pi-rogs گرد می خورد، شما پی می کنید، همیشه Pi-vo، و هنگامی که آنها با هم ملاقات می کنند صدای Pi را در می آورد.
طرفداران برای به خاطر سپردن نشانه های پی با هم رقابت خواهند کرد. و آنها سعی خواهند کرد از رکورد دانشجوی 24 ساله چینی لیو چائو که 68890 کاراکتر را بدون خطا از حافظه نام برده است، پیشی بگیرند. 24 ساعت و 4 دقیقه طول کشید.
خروج جشن ها برای 14 مارس برنامه ریزی شده است - تاریخی که در نوشتار آمریکایی مانند 3.14 به نظر می رسد - یعنی سه رقم اول پی.
طبق افسانه، کاهنان بابلی عدد "پی" را می دانستند. در ساخت و ساز استفاده می شود برج بابل. اما آنها قادر به محاسبه دقیق ارزش آن نبودند و به همین دلیل نتوانستند پروژه را تکمیل کنند. نماد عدد پی اولین بار در نوشته های او در سال 1706 توسط ریاضیدان ویلیام جونز استفاده شد. اما واقعاً پس از سال 1737 به لطف تلاش های ریاضیدان سوئدی لئونارد اویلر ریشه گرفت.
من ایده جشن گرفتن تعطیلات را داشتم فیزیکدان آمریکاییلری شاو
پاسخ دقیقی برای این سوال وجود ندارد که عدد "Pi" چند رقم اعشار دارد. به احتمال زیاد آنها عدد بی نهایت. آ ویژگی اصلیاین است که توالی این علائم تکرار نمی شود. امروزه 12411 تریلیون شناخته شده است. 500 میلیارد مورد بررسی قرار گرفت. و هیچ تکراری پیدا نشد.
به گفته برخی از فیزیکدانان و ریاضیدانان برجسته، به عنوان مثال دیوید بیلی، پیتر بوروین، سیمون پلوف، هیچ کس هرگز آنها را - تکرارها - پیدا نخواهد کرد. حداقل تمام کائنات را با نشانه ها بنویسید. بله، حداقل چند عالم... و دانشمندان عرفان پنهانی در این می بینند. اعتقاد بر این است که عدد "Pi" هرج و مرج اولیه بی پایان را رمزگذاری می کند که بعدها به هارمونی تبدیل شد. یا اطلاعات مرموز.

سوالات:
- تعریف دایره و دایره را فرموله کنید؟
- با چه مفاهیم جدیدی آشنا شدید؟
- مکان نقاط چه نامیده می شود؟
- تفاوت بین قطر و شعاع چیست؟
- چگونه شعاع دایره ای که با یک مثلث محصور شده است را پیدا کنیم؟
فهرست منابع مورد استفاده:
- درس با موضوع "هندسه بصری"
- ساوین A.P. روش مکان های هندسی / دوره اختیاریریاضیات: آموزشبرای پایه های 7-9 دبیرستان. Comp. آی.ال. نیکولسکایا. - م .: اشراق، ص 138. 74.
- اسمیرنوا I.M., Smirnov V.A. هندسه: کتاب درسی برای پایه های 7-9 موسسات آموزشی. - M.: Mnemosyne، 2005، ص. 84.
- شاریگین I.F. هندسه. پایه های 7-9: کتاب درسی برای آموزش عمومی موسسات آموزشی. - م.: بوستارد، ص. 76.
- Mazur K. I. "حل مسائل اصلی مسابقه در ریاضیات مجموعه ویرایش شده توسط M. I. Skanavi"
روی درس کار کرد:
سامیلینا ام.وی.
پوتورناک اس.ا.
ولادیمیر لاگوفسکی
سوال بپرسید در مورد آموزش مدرن، بیان یک ایده یا حل یک مشکل مبرم، می توانید انجمن آموزشی، کجا سطح بین المللیشورای آموزشی اندیشه و عمل تازه در حال جمع شدن است. ایجاد کرده است وبلاگ،شما نه تنها وضعیت خود را به عنوان یک معلم شایسته بهبود خواهید بخشید، بلکه سهم قابل توجهی در توسعه مدرسه آینده خواهید داشت. انجمن صنفی رهبران آموزشیدرها را به روی متخصصان باز می کند بالاترین رتبهو شما را به همکاری در ایجاد بهترین مدارس جهان دعوت می کند.
داشتن مقداری ملک
مثال ها [ | ]
تعریف رسمی[ | ]
که در مورد کلی، مکان هندسی نقاط توسط محمولی که استدلال آن نقطه ای در یک فضای خطی معین است فرموله می شود. پارامترهای محمول می تواند باشد نوع مختلف. محمول نامیده می شود تعیین کنندهمکان نقاط پارامترهای محمول نامیده می شوند دیفرانسیل هامنبع نقاط (نباید با دیفرانسیل در تحلیل اشتباه گرفته شود).
نقش دیفرانسیل ها در معرفی تفاوت گونه ها در شکل. تعداد دیفرانسیل ها می تواند هر کدام باشد. ممکن است اصلاً تفاوتی وجود نداشته باشد.
اگر تعیین کننده داده شود، کجا M (\displaystyle M)- نقطه، - دیفرانسیل، سپس شکل مورد نظر A (\displaystyle A)در فرم مشخص شده است: A (\displaystyle A)- مکان نقاط M (\displaystyle M)، به طوری که P (M , a , b , c ,…) (\displaystyle P(M,\;a,\;b,\;c,\;\ldots))" بعد، معمولاً نقش دیفرانسیل ها نشان داده می شود، نام آنها در رابطه با این رقم خاص داده می شود. خود شکل به عنوان مجموعه (مجموعه) نقاط درک می شود M (\displaystyle M)، که برای هر مجموعه ای از مقادیر خاص a , b , c , … (\displaystyle a,\;b,\;c,\;\ldots)بیانیه P (M , a , b , c ,…) (\displaystyle P(M,\;a,\;b,\;c,\;\ldots))به هویت تبدیل می شود هر مجموعه خاصی از مقادیر دیفرانسیل یک شکل جداگانه را تعریف می کند که هر یک و همه آنها با هم نام شکل نامیده می شود که از طریق GMT مشخص می شود.
به شکل کلامی قول اعتباریبیان ادبی، یعنی استفاده از انواع عبارات و غیره به منظور همخوانی. گاهی اوقات، در مورد تعیین کننده های ساده، آنها اصلاً بدون تعیین حروف انجام می دهند.
مثال: یک سهمی را به عنوان مجموعه ای از این نقاط تعریف می کنیم M (\displaystyle M)از چه فاصله ای است M (\displaystyle M)به نقطه F (\displaystyle F)برابر فاصله از M (\displaystyle M)به یک خط مستقیم l (\displaystyle l). سپس دیفرانسیل سهمی است F (\displaystyle F)و l (\displaystyle l); تعیین کننده - محمول P (M , F , l) = (ρ (M , F) = ρl (M , l)) (\displaystyle P(M,\;F,\;l)=(\rho (M,\;F) )=\rho _(l)(M,\;l)))، جایی که ρ (\displaystyle \rho)- فاصله بین دو نقطه (متریک) ρ l (\displaystyle \rho _(l))- فاصله از یک نقطه تا یک خط و می گویند: سهمی محل نقاط است M (\displaystyle M)، فاصله یکسان از نقطه F (\displaystyle F)و مستقیم l (\displaystyle l). توقف کامل F (\displaystyle F)کانون سهمی و خط مستقیم نامیده می شود l (\displaystyle l)- مدیر مدرسه."
مکان هندسی نقاط (از این پس GMT) شکل صفحه ای است که از نقاطی تشکیل شده است که دارای خاصیت خاصی هستند و شامل یک نقطه واحد نیست که این ویژگی را نداشته باشد.
ما فقط آن دسته از HMT هایی را در نظر خواهیم گرفت که می توانند با استفاده از قطب نما و خط کش ساخته شوند.
اجازه دهید HMT ها را در یک هواپیما در نظر بگیریم که ساده ترین و متداول ترین ویژگی ها را دارند:
1) GMT های واقع در فاصله معین r از یک نقطه مشخص O دایره ای با مرکز در نقطه O با شعاع r هستند.
2) GMT با فاصله مساوی از دو نقطه داده شده A و B خط مستقیمی است عمود بر قطعه AB و از وسط آن می گذرد.
3) GMT با فاصله مساوی از دو خط متقاطع داده شده، یک جفت خط متقابل عمود وجود دارد که از نقطه تقاطع می گذرد و زوایای بین خطوط داده شده را به نصف تقسیم می کند.
4) HMT ها که در همان فاصله h از خط مستقیم قرار دارند، دارای دو خط مستقیم موازی با این خط مستقیم و در امتداد هستند. طرف های مختلفاز آن در یک فاصله معین h.
5) مکان هندسی مراکز دایره های مماس بر یک خط معین m در نقطه معین M روی آن بر AB در نقطه M عمود است (به جز نقطه M).
6) مکان هندسی مراکز دایره های مماس بر یک دایره معین در یک نقطه معین M روی آن خط مستقیمی است که از نقطه M و مرکز دایره داده شده می گذرد (به جز نقاط M و O).
7) GMT، که بخش معینی از آن در یک زاویه مشخص قابل مشاهده است، دو کمان دایره ای را تشکیل می دهد که در یک قطعه مشخص توصیف شده و حاوی یک زاویه مشخص است.
8) GMT، فاصله ای که از آن به دو نقطه داده شده A و B به نسبت m: n است، یک دایره است (به نام دایره آپولونیوس).
9) مکان هندسی نقاط میانی وترهای ترسیم شده از یک نقطه دایره دایره ای است که بر روی یک پاره متصل ساخته شده است. این نقطهبا مرکز یک دایره معین، مانند قطر.
10) مكان هندسي رئوس مثلثها از نظر اندازه برابر با داده شده و داراي زمینه های مشترک، دو خط مستقیم می سازد، به موازات پایهو عبور از بالا مثلث داده شدهو متقارن به آن نسبت به خط مستقیم حاوی پایه است.
اجازه دهید مثال هایی از پیدا کردن GMT ارائه دهیم.
مثال 2.GMT هایی را پیدا کنید که نقطه میانی آکوردها هستند،از یک نقطه از یک دایره مشخص کشیده شده است(GMT شماره 9).
راه حل . بگذارید دایره ای با مرکز O داده شود و نقطه A روی این دایره که آکوردها از آن رسم می شوند انتخاب شود. اجازه دهید نشان دهیم که GMT مورد نظر دایره ای است که روی AO به عنوان قطر (به جز نقطه A) ساخته شده است (شکل 3).
بگذارید AB یک وتر و M نقطه وسط آن باشد. بیایید M و O را به هم وصل کنیم. سپس MO ^ AB (شعاع تقسیم وتر به دو نیم عمود بر این وتر است). اما پس از آن RAMO = 90 0. این بدان معنی است که M متعلق به دایره ای با قطر AO (GMT شماره 7) است. زیرا این دایره از نقطه O عبور می کند، سپس O به GMT ما تعلق دارد.
برعکس، اجازه دهید M به GMT ما تعلق داشته باشد. سپس، با کشیدن وتر AB از طریق M و اتصال M و O، به دست می آوریم که RAMO = 90 0، یعنی. MO ^ AB و بنابراین M وسط وتر AB است. اگر M با O منطبق باشد، O وسط AC است.
اغلب روش مختصات به فرد امکان می دهد GMT را پیدا کند.
مثال 3.GMT را پیدا کنید، فاصله ای که تا دو نقطه داده شده A و B در آن قرار دارند در این رابطه m: n (m ≠ n).

راه حل . بیایید انتخاب کنیم سیستم مستطیل شکلمختصات به طوری که نقاط A و B بر روی محور Ox به طور متقارن نسبت به مبدا قرار می گیرند و محور Oy از وسط AB عبور می کند (شکل 4). اجازه دهید AB = 2a. سپس نقطه A دارای مختصات A (a, 0) و نقطه B دارای مختصات B (-a, 0) است. فرض کنید C متعلق به HMT ما باشد، مختصات C(x، y) و CB/CA = m/nولی ![]()
![]() به معنای
به معنای
 (*)
(*)
بیایید برابری خود را متحول کنیم. ما داریم












