Kann man einen Kreis um ein Trapez beschreiben? Trapez. Vollständiger illustrierter Leitfaden (2019). Schutz personenbezogener Daten

Projektarbeit « Interessante Immobilien Trapeze » Abgeschlossen von: Schülerinnen der 10. Klasse Kudzaeva Ellina Bazzaeva Diana MKOU Secondary School s. N.Batako Leitung: Gagieva A.O. 20. November 2015

Zweck der Arbeit: Betrachten Sie die Eigenschaften des Trapezes, das Schulkurs Geometrien werden nicht untersucht, sondern bei der Lösung geometrischer Probleme mit dem Einheitlichen Staatsexamen Ab dem erweiterten Teil C 4 kann es erforderlich sein, genau diese Eigenschaften zu kennen und anwenden zu können.

Eigenschaften eines Trapezes: Wenn ein Trapez durch eine Linie parallel zu seinen Basen, gleich a und b, in zwei Teile geteilt wird flächengleiche Trapeze. Dann ist das zwischen den Seitenflächen eingeschlossene Segment zu dieser Linie gleich einem B to

Eigenschaft einer Strecke, die durch den Schnittpunkt der Diagonalen eines Trapezes verläuft. Liniensegment, parallel zu den Basen, durch den Schnittpunkt der Diagonalen verlaufend, ist gleich: a in c

Eigenschaften eines Trapezes: Ein gerades Liniensegment parallel zu den Basen eines Trapezes, das im Inneren des Trapezes eingeschlossen ist, wird durch seine Diagonalen in drei Teile geteilt. Dann sind die an den Seiten angrenzenden Segmente einander gleich. MP=OK R M O K

Eigenschaften eines gleichschenkligen Trapezes: Wenn ein Kreis in ein Trapez eingeschrieben werden kann, dann ist der Radius des Kreises der Durchschnitt proportional zu den Segmenten, in die der Berührungspunkt die Seite teilt. O S V A D. E O

Eigenschaften eines gleichschenkligen Trapezes: Liegt der Mittelpunkt des umschriebenen Kreises an der Basis des Trapezes, dann steht seine Diagonale senkrecht auf der Seite O A B C D

Eigenschaften eines gleichschenkligen Trapezes: Ein Kreis kann in ein gleichschenkliges Trapez eingeschrieben werden, wenn Seite gleich seiner Mittellinie. S V A D h

1)Wenn die Problemstellung besagt, dass ein Kreis in ein rechteckiges Trapez eingeschrieben ist, können Sie verwenden folgende Eigenschaften: 1. Die Summe der Grundflächen eines Trapezes ist gleich der Summe der Seiten. 2. Die Abstände vom Scheitelpunkt des Trapezes zu den Tangentialpunkten des eingeschriebenen Kreises sind gleich. 3. Höhe rechteckiges Trapez gleich seiner kleineren Seite und gleich dem Durchmesser des eingeschriebenen Kreises. 4. Der Mittelpunkt des eingeschriebenen Kreises ist der Schnittpunkt der Winkelhalbierenden des Trapezes. 5. Wenn der Tangentenpunkt die Seite in Segmente m und n teilt, dann ist der Radius des eingeschriebenen Kreises gleich

Eigenschaften eines rechteckigen Trapezes, in das ein Kreis eingeschrieben ist: 1) Ein Viereck, das aus dem Mittelpunkt des eingeschriebenen Kreises, den Kontaktpunkten und der Spitze des Trapezes besteht – ein Quadrat, dessen Seite gleich dem Radius ist. (AMOE und BKOM sind Quadrate mit der Seite r). 2) Wenn ein Kreis in ein rechteckiges Trapez eingeschrieben ist, dann ist die Fläche des Trapezes gleich dem Produkt seiner Basen: S=AD*BC

Beweis: Die Fläche eines Trapezes ist gleich dem Produkt aus der halben Summe seiner Grundflächen und seiner Höhe: Bezeichnen wir CF=m, FD=n. Da die Abstände von den Scheitelpunkten zu den Tangentenpunkten gleich sind, ist die Höhe des Trapezes gleich zwei Radien des eingeschriebenen Kreises und

I. Die Winkelhalbierenden an der lateralen Seite des Trapezes schneiden sich in einem Winkel von 90°. 1)∠ABC+∠BAD=180º (als interne Einseitigkeit mit AD∥BC und Sekante AB). 2) ∠ABK+∠KAB=(∠ABC+∠BAD):2=90º (da die Winkelhalbierenden die Winkel halbieren). 3) Da die Summe der Winkel eines Dreiecks 180º beträgt, gilt im Dreieck ABK: ∠ABK+∠KAB+∠AKB=180º, also ∠AKB=180-90=90º. Fazit: Die Winkelhalbierenden auf der lateralen Seite eines Trapezes schneiden sich im rechten Winkel. Diese Aussage wird beim Lösen von Problemen auf einem Trapez verwendet, in das ein Kreis eingeschrieben ist.

I I. Der Schnittpunkt der an die laterale Seite angrenzenden Trapezhalbierenden liegt auf der Mittellinie des Trapezes. Lassen Sie die Winkelhalbierende Winkel ABC schneidet die Seite AD im Punkt S. Dann ist das Dreieck ABS gleichschenklig mit der Basis BS. Das bedeutet, dass seine Winkelhalbierende AK auch ein Median ist, d. h. Punkt K ist der Mittelpunkt von BS. Wenn M und N die Mittelpunkte der Seiten des Trapezes sind, dann ist MN die Mittellinie des Trapezes und MN∥AD. Da M und K die Mittelpunkte von AB und BS sind, ist MK die Mittellinie des Dreiecks ABS und MK∥AS. Da durch den Punkt M nur eine Parallele zu dieser gezogen werden kann, liegt der Punkt K auf der Mittellinie des Trapezes.

III. Der Schnittpunkt der Winkelhalbierenden spitzer Winkel an der Basis eines Trapezes gehört zu einer anderen Basis. In diesem Fall sind die Dreiecke ABK und DCK gleichschenklig mit den Basen AK bzw. DK. Somit ist BC=BK+KC=AB+CD. Fazit: Wenn sich die Winkelhalbierenden eines Trapezes in einem Punkt schneiden, der zur kleineren Basis gehört, dann ist die kleinere Basis gleich der Summe der Seiten des Trapezes. Ein gleichschenkliges Trapez hat in diesem Fall eine kleinere Basis, die doppelt so groß ist wie seine Seite.

I V. Schnittpunkt der Winkelhalbierenden stumpfe Winkel an der Basis des Trapezes gehört es zu einer anderen Basis. In diesem Fall sind die Dreiecke ABF und DCF gleichschenklig mit den Basen BF bzw. CF. Daher AD=AF+FD=AB+CD. Fazit: Wenn sich die Winkelhalbierenden eines Trapezes in einem Punkt schneiden, der zu gehört mehr Grund, dann ist die größere Basis gleich der Summe der Seiten des Trapezes. In diesem Fall hat das gleichschenklige Trapez eine größere Basis, die doppelt so groß ist wie seine Seite.

Wenn ein gleichschenkliges Trapez mit Seiten a, b, c, d eingeschrieben und Kreise um ihn herum beschrieben werden können, dann ist die Fläche des Trapezes gleich

Umschriebener Kreis und Trapez. Guten Tag! Für Sie gibt es noch eine weitere Veröffentlichung, in der wir uns mit Problemen mit Trapezen befassen. Die Aufgaben sind Teil der Mathematikprüfung. Hier sind sie zu einer Gruppe zusammengefasst; es ist nicht nur ein Trapez gegeben, sondern eine Kombination von Körpern – ein Trapez und ein Kreis. Die meisten dieser Probleme werden mündlich gelöst. Aber es gibt auch einige, die angegangen werden müssen. Besondere Aufmerksamkeit, zum Beispiel Aufgabe 27926.

An welche Theorie müssen Sie sich erinnern? Das:

Probleme mit Trapezen, die auf dem Blog verfügbar sind, können eingesehen werden Hier.

27924. Um ein Trapez wird ein Kreis beschrieben. Der Umfang des Trapezes beträgt 22, die Mittellinie beträgt 5. Finden Sie die Seite des Trapezes.

Beachten Sie, dass ein Kreis nur um ein gleichschenkliges Trapez beschrieben werden kann. Wir erhalten die Mittellinie, was bedeutet, dass wir die Summe der Basen bestimmen können, also:

Das bedeutet, dass die Summe der Seiten 22–10=12 (Umfang minus Grundfläche) beträgt. Da die Seiten eines gleichschenkligen Trapezes gleich sind, ist eine Seite gleich sechs.

27925. Die laterale Seite eines gleichschenkligen Trapezes ist gleich seiner kleineren Basis, der Winkel an der Basis beträgt 60 0, die größere Basis beträgt 12. Finden Sie den Umkreis dieses Trapezes.

Wenn Sie Probleme mit einem Kreis und einem darin eingeschriebenen Sechseck gelöst haben, werden Sie sofort die Antwort aussprechen: Der Radius beträgt 6. Warum?

Sehen: gleichschenkliges Trapez mit einem Basiswinkel von 60 0 und gleiche Seiten AD, DC und CB stellen die Hälfte eines regelmäßigen Sechsecks dar:

In einem solchen Sechseck verläuft das Segment, das gegenüberliegende Eckpunkte verbindet, durch den Mittelpunkt des Kreises. *Der Mittelpunkt des Sechsecks und der Mittelpunkt des Kreises fallen zusammen, weitere Details

Das heißt, die größere Basis dieses Trapezes stimmt mit dem Durchmesser des umschriebenen Kreises überein. Der Radius beträgt also sechs.

*Natürlich können wir die Gleichheit der Dreiecke ADO, DOC und OCB berücksichtigen. Beweisen Sie, dass sie gleichseitig sind. Schließen Sie als Nächstes, dass der Winkel AOB gleich 180 0 ist und Punkt O von den Eckpunkten A, D, C und B gleich weit entfernt ist, und daher AO=OB=12/2=6.

27926. Die Grundflächen eines gleichschenkligen Trapezes sind 8 und 6. Der Radius des umschriebenen Kreises beträgt 5. Ermitteln Sie die Höhe des Trapezes.

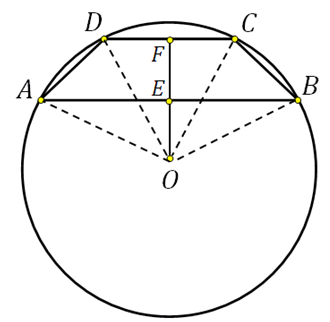
Beachten Sie, dass der Mittelpunkt des umschriebenen Kreises auf der Symmetrieachse liegt. Wenn wir die Höhe des Trapezes konstruieren, das durch diesen Mittelpunkt geht, teilt es diese beim Schnittpunkt mit den Grundflächen in zwei Hälften. Lassen Sie uns dies in der Skizze zeigen und auch den Mittelpunkt mit den Eckpunkten verbinden:

Das Segment EF ist die Höhe des Trapezes, wir müssen es finden.

IN rechtwinkliges Dreieck OFC kennen wir die Hypotenuse (das ist der Radius des Kreises), FC=3 (da DF=FC). Mit dem Satz des Pythagoras können wir OF berechnen:

Im rechtwinkligen Dreieck OEB kennen wir die Hypotenuse (das ist der Radius des Kreises), EB=4 (da AE=EB). Mit dem Satz des Pythagoras können wir OE berechnen:

Also EF=FO+OE=4+3=7.

Nun eine wichtige Nuance!

Bei diesem Problem zeigt die Abbildung deutlich, dass die Basen entlang liegen verschiedene Seiten vom Mittelpunkt des Kreises aus, daher wird das Problem auf diese Weise gelöst.

Was wäre, wenn die Bedingungen keine Skizze enthielten?

Dann hätte das Problem zwei Antworten. Warum? Schauen Sie genau hin – zwei Trapeze mit vorgegebenen Grundflächen können in jeden Kreis eingeschrieben werden:

*Das heißt, wenn man die Grundflächen des Trapezes und den Radius des Kreises berücksichtigt, gibt es zwei Trapeze.

Und die Lösung für die „zweite Option“ wird wie folgt sein.

Mit dem Satz des Pythagoras berechnen wir OF:

Berechnen wir auch OE:

Also EF=FO–OE=4–3=1.

Natürlich kann es bei einer kurzen Antwortaufgabe im Einheitlichen Staatsexamen nicht zwei Antworten geben, und ähnliche Aufgabe wird ohne Skizze nicht gegeben. Achten Sie deshalb besonders auf die Skizze! Nämlich: wie die Basen des Trapezes liegen. Bei Aufgaben mit detaillierter Antwort war dies jedoch in den vergangenen Jahren der Fall (mit etwas komplizierterer Bedingung). Wer nur eine Option für die Lage des Trapezes in Betracht gezogen hat, hat bei dieser Aufgabe einen Punkt verloren.

27937. Ein Trapez wird um einen Kreis herum beschrieben, dessen Umfang 40 beträgt. Finden Sie es Mittellinie.

Hier sollten wir uns sofort an die Eigenschaft eines um einen Kreis umschriebenen Vierecks erinnern:

Beträge gegenüberliegende Seiten Jedes um einen Kreis umschriebene Viereck ist gleich.

Guten Abend! Oh, diese umschriebenen oder eingeschriebenen Kreise, geometrische Figuren. Es ist so schwer, verwirrt zu werden. was und wann.

Versuchen wir es zunächst mit dem Wortlaut herauszufinden. Wir erhalten einen umschriebenen Kreis. Mit anderen Worten: Dieses Trapez ist in einen Kreis eingeschrieben.

Denken wir daran, dass wir nur einen Kreis beschreiben können. Ein gleichschenkliges Trapez wiederum ist ein Trapez, dessen Seiten gleich sind.

Versuchen wir, das Problem zu lösen. Wir wissen, dass die Basen des gleichschenkligen Trapezes ADCB 6 (DC) und 4 (AB) sind. Und der Radius des umschriebenen Kreises beträgt 4. Sie müssen die Höhe des Trapezes FK ermitteln.

FK ist die Höhe des Trapezes. Wir müssen es finden, aber denken Sie vorher daran, dass Punkt O der Mittelpunkt des Kreises ist. A OS, OD, OA, OB - bekannte Radien.

In OFC kennen wir die Hypotenuse, die den Radius des Kreises darstellt, und den Schenkel FC = halbe Basis DC = 3 cm (da DF = FC).

Finden wir nun OF:

Und im rechtwinkligen Dreieck OKB kennen wir auch die Hypotenuse, da dies der Radius des Kreises ist. Und KB ist gleich der Hälfte AB; KB = 2 cm. Und mit dem Satz des Pythagoras berechnen wir das Segment OK:

In diesem Artikel werden wir versuchen, die Eigenschaften eines Trapezes möglichst vollständig wiederzugeben. Insbesondere werden wir darüber sprechen allgemeine Zeichen und Eigenschaften eines Trapezes, sowie über die Eigenschaften eines eingeschriebenen Trapezes und über einen in ein Trapez eingeschriebenen Kreis. Wir werden auch auf die Eigenschaften eines gleichschenkligen und rechteckigen Trapezes eingehen.

Ein Beispiel für die Lösung eines Problems mithilfe der besprochenen Eigenschaften hilft Ihnen, es in Ihrem Kopf einzuordnen und sich den Stoff besser zu merken.

Trapez und Alles-Alles-Alles

Erinnern wir uns zunächst kurz daran, was ein Trapez ist und welche anderen Konzepte damit verbunden sind.

Ein Trapez ist also eine viereckige Figur, deren zwei Seiten parallel zueinander sind (das sind die Grundflächen). Und die beiden sind nicht parallel – das sind die Seiten.

Bei einem Trapez kann die Höhe abgesenkt werden – senkrecht zu den Grundflächen. Die Mittellinie und Diagonalen werden eingezeichnet. Es ist auch möglich, aus jedem Winkel des Trapezes eine Winkelhalbierende zu zeichnen.

Um verschiedene Eigenschaften, verbunden mit all diesen Elementen und ihren Kombinationen, werden wir jetzt sprechen.

Eigenschaften von Trapezdiagonalen

Um es klarer zu machen, skizzieren Sie beim Lesen das Trapez ACME auf einem Blatt Papier und zeichnen Sie Diagonalen hinein.

1. Wenn Sie die Mittelpunkte jeder Diagonale finden (nennen wir diese Punkte X und T) und sie verbinden, erhalten Sie ein Segment. Eine der Eigenschaften der Diagonalen eines Trapezes besteht darin, dass das Segment HT auf der Mittellinie liegt. Und seine Länge kann man erhalten, indem man die Differenz der Basen durch zwei dividiert: ХТ = (a – b)/2.
2. Vor uns liegt das gleiche Trapez ACME. Die Diagonalen schneiden sich im Punkt O. Schauen wir uns die Dreiecke AOE und MOK an, die aus Segmenten der Diagonalen zusammen mit den Basen des Trapezes gebildet werden. Diese Dreiecke sind ähnlich. Der Ähnlichkeitskoeffizient k von Dreiecken wird durch das Verhältnis der Basen des Trapezes ausgedrückt: k = AE/KM.
   Das Verhältnis der Flächen der Dreiecke AOE und MOK wird durch den Koeffizienten k 2 beschrieben.
3. Das gleiche Trapez, die gleichen Diagonalen, die sich im Punkt O schneiden. Nur dieses Mal betrachten wir die Dreiecke, die die Segmente der Diagonalen zusammen mit den Seiten des Trapezes bilden. Die Flächen der Dreiecke AKO und EMO sind gleich groß – ihre Flächen sind gleich.
4. Eine weitere Eigenschaft eines Trapezes ist die Konstruktion von Diagonalen. Wenn Sie also die Seiten von AK und ME in Richtung der kleineren Basis fortsetzen, werden sie sich früher oder später an einem bestimmten Punkt kreuzen. Zeichnen Sie als nächstes eine gerade Linie durch die Mitte der Basis des Trapezes. Es schneidet die Basen an den Punkten X und T.
   Wenn wir nun die Linie XT verlängern, dann verbindet sie den Schnittpunkt der Diagonalen des Trapezes O, den Punkt, an dem sich die Verlängerungen der Seiten und die Mitten der Grundflächen X und T schneiden.
5. Durch den Schnittpunkt der Diagonalen zeichnen wir ein Segment, das die Basen des Trapezes verbindet (T liegt auf der kleineren Basis KM, X auf der größeren AE). Der Schnittpunkt der Diagonalen teilt dieses Segment im folgenden Verhältnis: TO/OX = KM/AE.
6. Nun zeichnen wir durch den Schnittpunkt der Diagonalen ein Segment parallel zu den Grundflächen des Trapezes (a und b). Der Schnittpunkt teilt es in zwei gleiche Teile. Die Länge des Segments können Sie mithilfe der Formel ermitteln 2ab/(a + b).

Eigenschaften der Mittellinie eines Trapezes

Zeichnen Sie die Mittellinie im Trapez parallel zu seinen Basen.

1. Die Länge der Mittellinie eines Trapezes kann berechnet werden, indem die Längen der Basen addiert und in zwei Hälften geteilt werden: m = (a + b)/2.
2. Wenn Sie ein beliebiges Segment (zum Beispiel eine Höhe) durch beide Basen des Trapezes zeichnen, wird es durch die Mittellinie in zwei gleiche Teile geteilt.

Winkelhalbierendeigenschaft eines Trapezes

Wählen Sie eine beliebige Ecke des Trapezes aus und zeichnen Sie eine Winkelhalbierende. Nehmen wir zum Beispiel den Winkel KAE unseres Trapezes ACME. Nachdem Sie die Konstruktion selbst abgeschlossen haben, können Sie leicht überprüfen, ob die Winkelhalbierende von der Basis (oder ihrer Fortsetzung auf einer geraden Linie außerhalb der Figur selbst) ein Segment mit der gleichen Länge wie die Seite abschneidet.

Eigenschaften von Trapezwinkeln

1. Welches der beiden an die Seite angrenzenden Winkelpaare Sie auch wählen, die Summe der Winkel im Paar beträgt immer 180 0: α + β = 180 0 und γ + δ = 180 0.
2. Verbinden wir die Mittelpunkte der Basen des Trapezes mit einem Segment TX. Schauen wir uns nun die Winkel an den Basen des Trapezes an. Wenn die Summe der Winkel für einen von ihnen 90 0 beträgt, kann die Länge des Segments TX leicht berechnet werden, basierend auf der Differenz der Längen der Basen, geteilt in zwei Hälften: TX = (AE – KM)/2.
3. Wenn parallele Linien durch die Seiten eines Trapezwinkels gezogen werden, teilen sie die Seiten des Winkels in proportionale Segmente.

Eigenschaften eines gleichschenkligen (gleichseitigen) Trapezes

1. Bei einem gleichschenkligen Trapez sind die Winkel an jeder Basis gleich.
2. Bauen Sie jetzt noch einmal ein Trapez, damit Sie sich leichter vorstellen können, wovon wir sprechen. Schauen Sie sich die Basis von AE genau an – die Spitze gegenüberliegende Basis M wird auf einen bestimmten Punkt auf der Linie projiziert, die AE enthält. Der Abstand vom Scheitelpunkt A zum Projektionspunkt des Scheitelpunkts M und der Mittellinie eines gleichschenkligen Trapezes sind gleich.
3. Ein paar Worte zur Eigenschaft der Diagonalen eines gleichschenkligen Trapezes – ihre Längen sind gleich. Und auch die Neigungswinkel dieser Diagonalen zur Basis des Trapezes sind gleich.
4. Nur um ein gleichschenkliges Trapez kann ein Kreis beschrieben werden, da die Summe der entgegengesetzten Winkel eines Vierecks 180 0 beträgt – erforderliche Bedingung dafür.
5. Die Eigenschaft eines gleichschenkligen Trapezes ergibt sich aus dem vorherigen Absatz: Wenn ein Kreis in der Nähe des Trapezes beschrieben werden kann, ist er gleichschenklig.
6. Aus den Merkmalen eines gleichschenkligen Trapezes folgt die Eigenschaft der Höhe eines Trapezes: Wenn sich seine Diagonalen im rechten Winkel schneiden, dann ist die Länge der Höhe gleich der Hälfte der Summe der Basen: h = (a + b)/2.
7. Zeichnen Sie erneut das Segment TX durch die Mittelpunkte der Basen des Trapezes – bei einem gleichschenkligen Trapez steht es senkrecht zu den Basen. Und gleichzeitig ist TX die Symmetrieachse eines gleichschenkligen Trapezes.
8. Verringern Sie dieses Mal die Höhe vom gegenüberliegenden Scheitelpunkt des Trapezes auf die größere Basis (nennen wir es a). Sie erhalten zwei Segmente. Die Länge von Eins kann ermittelt werden, wenn die Längen der Basen addiert und in zwei Hälften geteilt werden: (a + b)/2. Den zweiten erhalten wir, wenn wir den kleineren von der größeren Basis subtrahieren und die resultierende Differenz durch zwei dividieren: (a – b)/2.

Eigenschaften eines in einen Kreis eingeschriebenen Trapezes

Da es sich bereits um ein in einen Kreis eingeschriebenes Trapez handelt, wollen wir uns näher mit diesem Thema befassen. Insbesondere, wo sich der Mittelpunkt des Kreises im Verhältnis zum Trapez befindet. Auch hier empfiehlt es sich, nicht faul zu sein, einen Bleistift zur Hand zu nehmen und zu zeichnen, wovon man spricht. wir werden reden unten. Auf diese Weise werden Sie schneller verstehen und sich besser erinnern.

1. Die Lage des Kreismittelpunkts wird durch den Neigungswinkel der Diagonale des Trapezes zu seiner Seite bestimmt. Beispielsweise kann eine Diagonale von der Oberseite eines Trapezes im rechten Winkel zur Seite verlaufen. In diesem Fall schneidet die größere Basis den Mittelpunkt des Kreises genau in der Mitte (R = ½AE).
2. Die Diagonale und die Seite können auch unten zusammentreffen spitzer Winkel– dann liegt der Mittelpunkt des Kreises innerhalb des Trapezes.
3. Der Mittelpunkt des umschriebenen Kreises kann außerhalb des Trapezes, jenseits seiner größeren Basis, liegen, wenn zwischen der Diagonale des Trapezes und der Seite ein stumpfer Winkel besteht.
4. Der Winkel zwischen der Diagonale und der größeren Basis des Trapezes ACME (eingeschriebener Winkel) beträgt die Hälfte Zentralwinkel, was ihm entspricht: MAE = ½MOE.
5. Kurz über zwei Möglichkeiten, den Radius eines umschriebenen Kreises zu ermitteln. Methode eins: Schauen Sie sich Ihre Zeichnung genau an – was sehen Sie? Sie können leicht erkennen, dass die Diagonale das Trapez in zwei Dreiecke teilt. Der Radius kann durch das Verhältnis der Dreiecksseite zum Sinus ermittelt werden entgegengesetzter Winkel, multipliziert mit zwei. Zum Beispiel, R = AE/2*sinAME. Auf ähnliche Weise kann die Formel für jede Seite beider Dreiecke geschrieben werden.
6. Methode zwei: Ermitteln Sie den Radius des umschriebenen Kreises durch die Fläche des Dreiecks. gebildet durch die Diagonale, Seite und Basis des Trapezes: R = AM*ME*AE/4*S AME.

Eigenschaften eines um einen Kreis umschriebenen Trapezes

Sie können einen Kreis in ein Trapez einpassen, wenn eine Bedingung erfüllt ist. Lesen Sie weiter unten mehr darüber. Und zusammengenommen hat diese Figurenkombination eine Reihe interessanter Eigenschaften.

1. Wenn ein Kreis in ein Trapez eingeschrieben ist, lässt sich die Länge seiner Mittellinie leicht ermitteln, indem man die Längen der Seiten addiert und die resultierende Summe in zwei Hälften teilt: m = (c + d)/2.
2. Bei einem trapezförmigen ACME, das um einen Kreis herum beschrieben wird, ist die Summe der Längen der Grundflächen gleich der Summe der Längen der Seiten: AK + ME = KM + AE.
3. Aus dieser Eigenschaft der Grundflächen eines Trapezes folgt die umgekehrte Aussage: Ein Kreis kann in ein Trapez eingeschrieben werden, dessen Grundsumme gleich der Summe seiner Seiten ist.
4. Der Tangentenpunkt eines Kreises mit dem Radius r, der in ein Trapez eingeschrieben ist, teilt die Seite in zwei Segmente, nennen wir sie a und b. Der Radius eines Kreises kann mit der Formel berechnet werden: r = √ab.
5. Und noch eine Immobilie. Um Verwirrung zu vermeiden, zeichnen Sie dieses Beispiel auch selbst. Wir haben das gute alte Trapez ACME, das um einen Kreis herum beschrieben wird. Es enthält Diagonalen, die sich im Punkt O schneiden. Die aus den Segmenten der Diagonalen und den Seitenflächen gebildeten Dreiecke AOK und EOM sind rechteckig.
   Die Höhen dieser Dreiecke, abgesenkt zu den Hypotenusen (d. h. den Seiten des Trapezes), stimmen mit den Radien des eingeschriebenen Kreises überein. Und die Höhe des Trapezes stimmt mit dem Durchmesser des eingeschriebenen Kreises überein.

Eigenschaften eines rechteckigen Trapezes

Ein Trapez heißt rechteckig, wenn einer seiner Winkel richtig ist. Und seine Eigenschaften ergeben sich aus diesem Umstand.

1. Bei einem rechteckigen Trapez steht eine Seite senkrecht zur Grundfläche.
2. Höhe und seitliche Seite des angrenzenden Trapezes rechter Winkel, sind gleich. Damit können Sie die Fläche eines rechteckigen Trapezes berechnen ( allgemeine Formel S = (a + b) * h/2) nicht nur durch die Höhe, sondern auch durch die an den rechten Winkel angrenzende Seite.
3. Für ein rechteckiges Trapez sind die oben bereits beschriebenen allgemeinen Eigenschaften der Diagonalen eines Trapezes relevant.

Hinweise auf einige Eigenschaften des Trapezes

Winkelgleichheit an der Basis eines gleichschenkligen Trapezes:

• Sie haben wahrscheinlich schon vermutet, dass wir hier wieder das AKME-Trapez benötigen – zeichnen Sie ein gleichschenkliges Trapez. Zeichnen Sie eine gerade Linie MT vom Scheitelpunkt M parallel zur Seite von AK (MT || AK).

Das resultierende Viereck AKMT ist ein Parallelogramm (AK || MT, KM || AT). Da ME = KA = MT, ist ∆ MTE gleichschenklig und MET = MTE.

AK || MT, daher MTE = KAE, MET = MTE = KAE.

Wobei AKM = 180 0 - MET = 180 0 - KAE = KME.

Q.E.D.

Basierend auf der Eigenschaft eines gleichschenkligen Trapezes (Gleichheit der Diagonalen) beweisen wir das nun Das Trapez ACME ist gleichschenklig:

• Zeichnen wir zunächst eine gerade Linie MX – MX || KE. Wir erhalten ein Parallelogramm KMHE (Basis – MX || KE und KM || EX).

∆AMX ist gleichschenklig, da AM = KE = MX und MAX = MEA.

MH || KE, KEA = MHE, also MAE = MHE.

Es stellte sich heraus, dass die Dreiecke AKE und EMA einander gleich sind, denn AM = KE und AE – gemeinsame Seite zwei Dreiecke. Und auch MAE = MXE. Wir können daraus schließen, dass AK = ME ist, und daraus folgt, dass das Trapez AKME gleichschenklig ist.

Überprüfungsaufgabe

Die Basen des Trapezes ACME betragen 9 cm und 21 cm, die Seitenlänge KA, gleich 8 cm, bildet mit der kleineren Basis einen Winkel von 150 0. Sie müssen die Fläche des Trapezes ermitteln.

Lösung: Vom Scheitelpunkt K verringern wir die Höhe zur größeren Basis des Trapezes. Und beginnen wir mit der Betrachtung der Winkel des Trapezes.

Die Winkel AEM und KAN sind einseitig. Das bedeutet, dass sie insgesamt 180 0 ergeben. Daher ist KAN = 30 0 (basierend auf der Eigenschaft der Trapezwinkel).

Betrachten wir nun das rechteckige ∆ANC (ich glaube, dieser Punkt ist für Leser ohne zusätzliche Beweise offensichtlich). Daraus ermitteln wir die Höhe des Trapezes KH – in einem Dreieck ist es ein Bein, das dem Winkel 30 0 gegenüberliegt. Daher ist KH = ½AB = 4 cm.

Wir ermitteln die Fläche des Trapezes mit der Formel: S ACME = (KM + AE) * KN/2 = (9 + 21) * 4/2 = 60 cm 2.

Nachwort

Wenn Sie diesen Artikel sorgfältig und sorgfältig studiert haben, nicht zu faul waren, mit einem Bleistift in der Hand Trapeze für alle angegebenen Eigenschaften zu zeichnen und sie in der Praxis zu analysieren, sollten Sie das Material gut beherrschen.

Natürlich gibt es hier viele Informationen, vielfältig und manchmal sogar verwirrend: Es ist nicht so schwer, die Eigenschaften des beschriebenen Trapezes mit den Eigenschaften des eingeschriebenen zu verwechseln. Aber Sie haben selbst gesehen, dass der Unterschied riesig ist.

Jetzt hast du ausführliche Zusammenfassung alle allgemeine Eigenschaften Trapeze. Und auch spezifische Eigenschaften und Zeichen von gleichschenkligen und rechteckigen Trapezen. Es eignet sich sehr gut zur Vorbereitung auf Tests und Prüfungen. Probieren Sie es selbst aus und teilen Sie den Link mit Ihren Freunden!

Wenn Sie Material ganz oder teilweise kopieren, ist ein Link zur Originalquelle erforderlich.

Ein Trapez ist eine geometrische Figur mit vier Winkeln. Bei der Konstruktion eines Trapezes ist zu berücksichtigen, dass zwei gegenüberliegende Seiten parallel sind, die anderen beiden hingegen nicht parallel zueinander. Dieses Wort stammt aus der Neuzeit Antikes Griechenland und klang wie „trapezion“, was „Tisch“, „Esstisch“ bedeutete.

In diesem Artikel geht es um die Eigenschaften eines um einen Kreis umschriebenen Trapezes. Wir werden uns auch die Typen und Elemente dieser Figur ansehen.

Elemente, Typen und Eigenschaften der geometrischen Figur Trapez

Parallele Seiten in dieser Abbildung werden die Basen genannt, und diejenigen, die nicht parallel sind, werden die Seiten genannt. Vorausgesetzt, dass die Seiten die gleiche Länge, das Trapez gilt als gleichschenklig. Ein Trapez, dessen Seiten senkrecht zur Grundfläche in einem Winkel von 90° stehen, wird als Rechteck bezeichnet.

Diese scheinbar einfache Figur weist eine beträchtliche Anzahl von Eigenschaften auf, die ihre Eigenschaften hervorheben:

1. Wenn Sie entlang der Seiten eine Mittellinie zeichnen, verläuft diese parallel zu den Basen. Dieses Segment entspricht der Hälfte der Differenz der Basen.
2. Wenn Sie eine Winkelhalbierende aus einem beliebigen Winkel eines Trapezes konstruieren, a gleichseitiges Dreieck.
3. Aus den Eigenschaften eines um einen Kreis beschriebenen Trapezes weiß man, dass die Summe der parallelen Seiten gleich der Summe der Grundflächen sein muss.
4. Beim Konstruieren diagonaler Segmente, bei denen eine der Seiten die Basis eines Trapezes ist, sind die resultierenden Dreiecke ähnlich.
5. Beim Konstruieren diagonaler Segmente, bei denen eine der Seiten seitlich ist, ergeben sich Dreiecke gleiche Fläche.
6. Wenn wir die Seitenlinien fortsetzen und ein Segment von der Mitte der Basis aus konstruieren, dann Winkel gebildet wird 90° betragen. Das die Basen verbindende Segment entspricht der Hälfte ihrer Differenz.

Eigenschaften eines um einen Kreis umschriebenen Trapezes

Das Einschließen eines Kreises in ein Trapez ist nur unter einer Bedingung möglich. Dieser Zustand ist, dass die Summe der Seiten gleich der Summe der Basen sein muss. Bei der Konstruktion eines trapezförmigen AFDM gilt beispielsweise AF + DM = FD + AM. Nur in diesem Fall kann ein Kreis in ein Trapez eingeschlossen werden.

Also, mehr über die Eigenschaften eines Trapezes, das um einen Kreis beschrieben wird:

1. Wenn ein Kreis von einem Trapez umgeben ist, muss man, um die Länge seiner Linie zu ermitteln, die die Figur in zwei Hälften schneidet, die Hälfte der Summe der Seitenlängen ermitteln.
2. Bei der Konstruktion eines um einen Kreis umschriebenen Trapezes ist die gebildete Hypotenuse identisch mit dem Radius des Kreises und die Höhe des Trapezes ist gleichzeitig der Durchmesser des Kreises.
3. Eine weitere Eigenschaft eines um einen Kreis umschriebenen gleichschenkligen Trapezes besteht darin, dass seine Seite vom Mittelpunkt des Kreises aus in einem Winkel von 90° sofort sichtbar ist.

Etwas mehr über die Eigenschaften eines in einem Kreis eingeschlossenen Trapezes

In einen Kreis kann nur ein gleichschenkliges Trapez eingeschrieben werden. Dies bedeutet, dass die Bedingungen erfüllt sein müssen, unter denen das konstruierte AFDM-Trapez erfüllt folgenden Anforderungen: AF + DM = FD + MA.

Der Satz des Ptolemäus besagt, dass bei einem in einem Kreis eingeschlossenen Trapez das Produkt der Diagonalen identisch und gleich der Summe der gegenüberliegenden Seiten multipliziert ist. Dies bedeutet, dass bei der Konstruktion eines um das Trapez AFDM umschriebenen Kreises gilt: AD × FM = AF × DM + FD × AM.

An Schulprüfungen Sehr oft gibt es Probleme, die eine Lösung mit einem Trapez erfordern. Große Menge Theoreme müssen auswendig gelernt werden, aber wenn man sie nicht sofort lernen kann, ist das egal. Es ist am besten, regelmäßig auf Hinweise in Lehrbüchern zurückzugreifen, damit dieses Wissen ganz natürlich und ohne Selbstverständlichkeit vermittelt wird besondere Arbeit Habe es in meinem Kopf.