Berechnung des Integrals mit der Newton-Leibniz-Formel. Definitives Integral online. Variablen in einem bestimmten Integral ändern

Problem 1(über die Berechnung der Fläche eines gekrümmten Trapezes).

Auf Kartesisch rechteckiges System Koordinaten xOy, eine durch die x-Achse begrenzte Figur (siehe Abbildung), gerade Linien x = a, x = b (ein gekrümmtes Trapez. Es ist erforderlich, die Fläche des gekrümmten Trapezes zu berechnen.
Lösung. Die Geometrie gibt uns Rezepte zur Berechnung der Flächen von Polygonen und einigen Teilen eines Kreises (Sektor, Segment). Mithilfe geometrischer Überlegungen können wir mit folgender Überlegung nur einen ungefähren Wert für die benötigte Fläche ermitteln.

Teilen wir das Segment [a; b] (Basis eines gebogenen Trapezes) auf n gleiche Teile; Diese Aufteilung erfolgt unter Verwendung der Punkte x 1, x 2, ... x k, ... x n-1. Durch diese Punkte ziehen wir gerade Linien parallel zur y-Achse. Dann wird das gegebene krummlinige Trapez in n Teile, in n schmale Spalten, unterteilt. Die Fläche des gesamten Trapezes ist gleich der Summe der Flächen der Säulen.

Betrachten wir die k-te Spalte separat, d.h. ein gebogenes Trapez, dessen Basis ein Segment ist. Ersetzen wir es durch ein Rechteck mit derselben Grundfläche und Höhe gleich f(x k) (siehe Abbildung). Die Fläche des Rechtecks ​​​​ist gleich \(f(x_k) \cdot \Delta x_k \), wobei \(\Delta x_k \) die Länge des Segments ist; Es ist selbstverständlich, das resultierende Produkt als ungefähren Wert der Fläche der k-ten Spalte zu betrachten.

Wenn wir nun das Gleiche mit allen anderen Spalten machen, kommen wir zu zum nächsten Ergebnis: Die Fläche S eines gegebenen krummlinigen Trapezes ist ungefähr gleich der Fläche S n einer Stufenfigur aus n Rechtecken (siehe Abbildung):
\(S_n = f(x_0)\Delta x_0 + \dots + f(x_k)\Delta x_k + \dots + f(x_(n-1))\Delta x_(n-1) \)
Aus Gründen der Einheitlichkeit der Notation gehen wir hier davon aus, dass a = x 0, b = x n; \(\Delta x_0 \) – Länge des Segments, \(\Delta x_1 \) – Länge des Segments usw.; in diesem Fall gilt, wie wir oben vereinbart haben, \(\Delta x_0 = \dots = \Delta x_(n-1) \)

Also gilt \(S \ approx S_n \), und diese ungefähre Gleichheit ist umso genauer, je größer n ist.
Per Definition wird angenommen, dass die erforderliche Fläche eines krummlinigen Trapezes gleich dem Grenzwert der Folge (S n) ist:
$$ S = \lim_(n \to \infty) S_n $$

Problem 2(über das Verschieben eines Punktes)
Bewegt sich in einer geraden Linie materieller Punkt. Die Abhängigkeit der Geschwindigkeit von der Zeit wird durch die Formel v = v(t) ausgedrückt. Finden Sie die Bewegung eines Punktes über einen bestimmten Zeitraum [a; B].
Lösung. Wäre die Bewegung gleichmäßig, dann wäre das Problem ganz einfach zu lösen: s = vt, d.h. s = v(b-a). Bei ungleichmäßiger Bewegung müssen Sie dieselben Ideen verwenden, auf denen die Lösung des vorherigen Problems basierte.
1) Teilen Sie das Zeitintervall [a; b] in n gleiche Teile.
2) Betrachten Sie einen Zeitraum und gehen Sie davon aus, dass die Geschwindigkeit während dieses Zeitraums konstant war, genau wie zum Zeitpunkt t k. Wir nehmen also an, dass v = v(t k).
3) Lassen Sie uns den ungefähren Wert der Bewegung des Punktes über einen bestimmten Zeitraum ermitteln. Wir bezeichnen diesen ungefähren Wert als s k
\(s_k = v(t_k) \Delta t_k \)
4) Ermitteln Sie den ungefähren Wert der Verschiebung s:
\(s \ approx S_n \) wobei
\(S_n = s_0 + \dots + s_(n-1) = v(t_0)\Delta t_0 + \dots + v(t_(n-1)) \Delta t_(n-1) \)
5) Die erforderliche Verschiebung ist gleich dem Grenzwert der Folge (S n):
$$ s = \lim_(n \to \infty) S_n $$

Fassen wir zusammen. Lösungen mehrere Aufgaben auf das gleiche mathematische Modell reduziert. Viele Probleme aus verschiedenen Bereichen der Wissenschaft und Technik führen im Lösungsprozess zum gleichen Modell. Also das mathematisches Modell müssen speziell untersucht werden.

Der Begriff eines bestimmten Integrals

Geben wir mathematische Beschreibung das Modell, das in den drei betrachteten Problemen für die Funktion y = f(x) erstellt wurde, stetig (aber nicht unbedingt nicht negativ, wie in den betrachteten Problemen angenommen wurde) auf dem Intervall [a; B]:
1) Teilen Sie das Segment [a; b] in n gleiche Teile;
2) Bilden Sie die Summe $$ S_n = f(x_0)\Delta x_0 + f(x_1)\Delta x_1 + \dots + f(x_(n-1))\Delta x_(n-1) $$
3) Berechnen Sie $$ \lim_(n \to \infty) S_n $$

Im Kurs mathematische Analyse Es wurde nachgewiesen, dass dieser Grenzwert im Fall einer stetigen (oder stückweise stetigen) Funktion existiert. Er heißt ein bestimmtes Integral der Funktion y = f(x) über die Strecke [a; B] und wie folgt bezeichnet:
\(\int\limits_a^b f(x) dx \)
Die Zahlen a und b werden Integrationsgrenzen (untere bzw. obere) genannt.

Kehren wir zu den oben besprochenen Aufgaben zurück. Die in Aufgabe 1 angegebene Flächendefinition kann nun wie folgt umgeschrieben werden:
\(S = \int\limits_a^b f(x) dx \)
hier ist S die Fläche des in der Abbildung oben gezeigten gebogenen Trapezes. Das ist geometrische Bedeutung bestimmtes Integral.

Die in Aufgabe 2 angegebene Definition der Verschiebung s eines Punktes, der sich geradlinig mit der Geschwindigkeit v = v(t) über den Zeitraum von t = a bis t = b bewegt, kann wie folgt umgeschrieben werden:

Newton-Leibniz-Formel

Beantworten wir zunächst die Frage: Welcher Zusammenhang besteht zwischen dem bestimmten Integral und der Stammfunktion?

Die Antwort findet sich in Aufgabe 2. Einerseits wird die Verschiebung s eines Punktes, der sich geradlinig mit der Geschwindigkeit v = v(t) über den Zeitraum von t = a bis t = b bewegt, durch berechnet die Formel
\(S = \int\limits_a^b v(t) dt \)

Andererseits ist die Koordinate eines sich bewegenden Punktes eine Stammfunktion für die Geschwindigkeit – nennen wir sie s(t); Dies bedeutet, dass die Verschiebung s durch die Formel s = s(b) - s(a) ausgedrückt wird. Als Ergebnis erhalten wir:
\(S = \int\limits_a^b v(t) dt = s(b)-s(a) \)
wobei s(t) die Stammfunktion von v(t) ist.

Der folgende Satz wurde im Zuge der mathematischen Analyse bewiesen.
Satz. Wenn die Funktion y = f(x) im Intervall [a; b], dann ist die Formel gültig
\(S = \int\limits_a^b f(x) dx = F(b)-F(a) \)
wobei F(x) die Stammfunktion von f(x) ist.

Die angegebene Formel wird normalerweise aufgerufen Newton-Leibniz-Formel zu Ehren Englischer Physiker Isaac Newton (1643–1727) und der deutsche Philosoph Gottfried Leibniz (1646–1716), die es unabhängig voneinander und nahezu gleichzeitig erhielten.

In der Praxis verwenden sie anstelle von F(b) - F(a) die Notation \(\left. F(x)\right|_a^b \) (manchmal auch so genannt). Doppelsubstitution) und schreiben Sie dementsprechend die Newton-Leibniz-Formel in dieser Form um:
\(S = \int\limits_a^b f(x) dx = \left. F(x)\right|_a^b \)

Wenn Sie ein bestimmtes Integral berechnen, ermitteln Sie zunächst die Stammfunktion und führen Sie dann eine Doppelsubstitution durch.

Basierend auf der Newton-Leibniz-Formel können wir zwei Eigenschaften des bestimmten Integrals erhalten.

Eigentum 1. Integral der Summe der Funktionen gleich der Summe Integrale:
\(\int\limits_a^b (f(x) + g(x))dx = \int\limits_a^b f(x)dx + \int\limits_a^b g(x)dx \)

Eigentum 2. Konstanter Multiplikator lässt sich aus dem Integralzeichen entnehmen:
\(\int\limits_a^b kf(x)dx = k \int\limits_a^b f(x)dx \)

Berechnen der Flächen ebener Figuren mithilfe eines bestimmten Integrals

Mit dem Integral können Sie nicht nur Flächen berechnen krummlinige Trapeze, aber auch flachere Figuren komplexer Typ, zum Beispiel das in der Abbildung gezeigte. Die Zahl P wird durch Geraden x = a, x = b und Graphen stetiger Funktionen y = f(x), y = g(x) und auf der Strecke [a; b] gilt die Ungleichung \(g(x) \leq f(x) \). Um die Fläche S einer solchen Figur zu berechnen, gehen wir wie folgt vor:
\(S = S_(ABCD) = S_(aDCb) - S_(aABb) = \int\limits_a^b f(x) dx - \int\limits_a^b g(x) dx = \)
\(= \int\limits_a^b (f(x)-g(x))dx \)

Also die Fläche S einer Figur, die durch Geraden x = a, x = b und Funktionsgraphen y = f(x), y = g(x) begrenzt wird, stetig auf dem Segment und so, dass für jedes x aus dem Segment [A; b] die Ungleichung \(g(x) \leq f(x) \) erfüllt ist, berechnet durch die Formel
\(S = \int\limits_a^b (f(x)-g(x))dx \)

Tabelle unbestimmter Integrale (Stammfunktionen) einiger Funktionen

$$ \int 0 \cdot dx = C $$ $$ \int 1 \cdot dx = x+C $$ $$ \int x^n dx = \frac(x^(n+1))(n+1 ) +C \;\; (n \neq -1) $$ $$ \int \frac(1)(x) dx = \ln |x| +C $$ $$ \int e^x dx = e^x +C $$ $$ \int a^x dx = \frac(a^x)(\ln a) +C \;\; (a>0, \;\; a \neq 1) $$ $$ \int \cos x dx = \sin x +C $$ $$ \int \sin x dx = -\cos x +C $$ $ $ \int \frac(dx)(\cos^2 x) = \text(tg) x +C $$ $$ \int \frac(dx)(\sin^2 x) = -\text(ctg) x +C $$ $$ \int \frac(dx)(\sqrt(1-x^2)) = \text(arcsin) x +C $$ $$ \int \frac(dx)(1+x^2 ) = \text(arctg) x +C $$ $$ \int \text(ch) x dx = \text(sh) x +C $$ $$ \int \text(sh) x dx = \text(ch ) x +C $$

Newton-Leibniz-Formel

Hauptsatz der Analyse oder Newton-Leibniz-Formel gibt eine Beziehung zwischen zwei Operationen an: die Bildung eines bestimmten Integrals und die Berechnung der Stammfunktion

Formulierung

Betrachten Sie das Integral der Funktion j = F(X) von konstante Zahl A bis zur Nummer X, die wir als variabel betrachten werden. Schreiben wir das Integral in das folgende Formular:

Dieser Typ Als Integral bezeichnet man ein Integral mit variabler Obergrenze. Mit dem Mittelwertsatz in einem bestimmten Integral lässt sich das leicht zeigen diese Funktion stetig und differenzierbar. Und auch die Ableitung einer gegebenen Funktion am Punkt x ist gleich der integrierbaren Funktion selbst. Daraus folgt, dass jede stetige Funktion eine Stammfunktion in Form einer Quadratur hat: . Und da sich die Klasse der Stammfunktionen der Funktion f um eine Konstante unterscheidet, lässt sich leicht zeigen, dass: das bestimmte Integral der Funktion f auf gleich der Differenz Werte der Stammfunktionen an den Punkten b und a

Wikimedia-Stiftung. 2010.

• Gesamtwahrscheinlichkeitsformel
• Rayleigh-Jeans-Formel

Sehen Sie, was die „Newton-Leibniz-Formel“ in anderen Wörterbüchern lautet:

Newton-Leibniz-Formel- Der Hauptsatz der Analyse oder Newtons Leibniz-Formel gibt die Beziehung zwischen zwei Operationen an: Nehmen eines bestimmten Integrals und Berechnen der Stammfunktion. Formulierung Betrachten wir das Integral der Funktion y = f(x) im Bereich von einer konstanten Zahl a bis... . ... Wikipedia

Formel für endliches Inkrement- Dieser Begriff hat andere Bedeutungen, siehe Satz von Lagrange. Die endliche Inkrementformel oder der Mittelwertsatz von Lagrange besagt, dass, wenn eine Funktion in einem Intervall stetig ist und... Wikipedia

Stokes-Formel- Der Satz von Stokes ist einer der Hauptsätze Differentialgeometrie und mathematische Analyse der Integration Differentialformen, das mehrere Theoreme der Analyse verallgemeinert. Benannt nach J. G. Stokes. Inhalt 1 Allgemeine Formulierung 2… … Wikipedia

NEWTON-LEIBNITZ-FORMEL- eine Formel, die den Wert eines bestimmten Integrals von ausdrückt gegebene Funktion f entlang einer Strecke in Form der Differenz der Werte an den Enden einer beliebigen Stammfunktion F dieser Funktion. Benannt nach I. Newton und G. Leibniz, weil die Regel... ... Mathematische Enzyklopädie

NEWTON-LEIBNITZ-FORMEL- Grundformel Integralrechnung. Drückt den Zusammenhang zwischen einem bestimmten Integral einer Funktion f(x) und einer ihrer Stammfunktionen F(x) aus ... Großes enzyklopädisches Wörterbuch

Leibniz-Formel- Dieser Begriff hat andere Bedeutungen, siehe Liste der nach Leibniz benannten Objekte. Dieser Begriff hat andere Bedeutungen, siehe Leibniz-Formel (Bedeutungen). Die Leibniz-Formel in der Integralrechnung ist die Regel... ... Wikipedia

Newton-Leibniz-Formel- Newton-Leibniz-Formel, die Grundformel der Integralrechnung. Drückt den Zusammenhang zwischen dem bestimmten Integral der Funktion f(x) und einer ihrer Stammfunktionen F(x) aus. . * * * NEWTON LEIBNITZ FORMEL NEWTON LEIBNITZ FORMEL, Grundformel... ... Enzyklopädisches Wörterbuch

Rechteckformel

Trapezformel - Bestimmtes Integral als Fläche der Figur Numerische Integration ( historischer Name: Quadratur) Berechnung des Wertes eines bestimmten Integrals (normalerweise ungefähr), basierend auf der Tatsache, dass der Wert des Integrals numerisch gleich der Fläche ist ... ... Wikipedia

Newtons Theorem- Newtons Leibniz-Formel oder der Grundsatz der Analysis gibt die Beziehung zwischen zwei Operationen an: die Bildung eines bestimmten Integrals und die Berechnung der Stammfunktion. Wenn es auf einem Segment stetig ist und jede Stammfunktion davon auf diesem Segment ... Wikipedia hat

Lösung angewandte Probleme kommt es darauf an, das Integral zu berechnen, aber es ist nicht immer möglich, dies genau zu tun. Manchmal ist es notwendig, den Wert eines bestimmten Integrals mit einer gewissen Genauigkeit zu kennen, beispielsweise bis zu einem Tausendstel.

Es gibt Probleme, wenn es notwendig wäre, den Näherungswert eines bestimmten Integrals mit der erforderlichen Genauigkeit zu ermitteln und dann zu verwenden numerische Integration wie die Simposn-Methode, Trapeze, Rechtecke. Nicht in allen Fällen ist eine Berechnung mit einer gewissen Genauigkeit möglich.

Dieser Artikel untersucht die Anwendung der Newton-Leibniz-Formel. Dies ist für die genaue Berechnung des bestimmten Integrals erforderlich. Wird gegeben werden detaillierte Beispiele, Änderungen der Variablen im bestimmten Integral werden berücksichtigt und wir finden die Werte des bestimmten Integrals bei der partiellen Integration.

Yandex.RTB R-A-339285-1

Newton-Leibniz-Formel

Definition 1

Wenn die Funktion y = y (x) vom Intervall [ a ; b ] , und F (x) ist einer von Stammfunktionen dieses Segment also Newton-Leibniz-Formel als gerecht angesehen. Schreiben wir es so: ∫ a b f (x) d x = F (b) - F (a) .

Diese Formel halten die Grundformel der Integralrechnung.

Um einen Beweis dieser Formel zu erbringen, ist es notwendig, das Konzept eines Integrals mit einer verfügbaren Variablenobergrenze zu verwenden.

Wenn die Funktion y = f (x) vom Intervall [ a ; b ], dann ist der Wert des Arguments x ∈ a; b , und das Integral hat die Form ∫ a x f (t) d t und wird als Funktion der Obergrenze betrachtet. Es ist notwendig, die Notation der Funktion anzunehmen, die die Form ∫ a x f (t) d t = Φ (x) annimmt, sie ist stetig und eine Ungleichung der Form ∫ a x f (t) d t " = Φ " (x) = f(x) gilt dafür.

Stellen wir fest, dass das Inkrement der Funktion Φ (x) dem Inkrement des Arguments ∆ x entspricht. Es ist notwendig, die fünfte Haupteigenschaft des bestimmten Integrals zu verwenden, und wir erhalten

Φ (x + ∆ x) - Φ x = ∫ a x + ∆ x f (t) d t - ∫ a x f (t) d t = = ∫ a x + ∆ x f (t) d t = f (c) x + ∆ x - x = f (c) ∆ x

wobei Wert c ∈ x; x + ∆ x .

Lassen Sie uns die Gleichheit in der Form Φ (x + ∆ x) - Φ (x) ∆ x = f (c) festlegen. Durch die Definition der Ableitung einer Funktion ist es notwendig, zum Grenzwert ∆ x → 0 zu gehen, dann erhalten wir eine Formel der Form Φ " (x) = f (x). Wir finden, dass Φ (x) ist eine der Stammfunktionen für eine Funktion der Form y = f (x), die sich auf [a; b] befindet

F (x) = Φ (x) + C = ∫ a x f (t) d t + C, wobei der Wert von C konstant ist.

Berechnen wir F (a) mithilfe der ersten Eigenschaft des bestimmten Integrals. Dann verstehen wir das

F (a) = Φ (a) + C = ∫ a a f (t) d t + C = 0 + C = C, daher erhalten wir C = F (a). Das Ergebnis ist bei der Berechnung von F (b) anwendbar und wir erhalten:

F (b) = Φ (b) + C = ∫ a b f (t) d t + C = ∫ a b f (t) d t + F (a), mit anderen Worten, F (b) = ∫ a b f (t) d t + F ( A) . Die Gleichheit wird durch die Newton-Leibniz-Formel ∫ a b f (x) d x + F (b) - F (a) bewiesen.

Wir nehmen das Inkrement der Funktion als F x a b = F (b) - F (a) an. Unter Verwendung der Notation hat die Newton-Leibniz-Formel die Form ∫ a b f (x) d x = F x a b = F (b) - F (a) .

Um die Formel anzuwenden, ist es notwendig, eine der Stammfunktionen y = F (x) der Integrandenfunktion y = f (x) aus dem Segment [ a ; b ], berechnen Sie das Inkrement der Stammfunktion aus diesem Segment. Schauen wir uns einige Beispiele für Berechnungen mit der Newton-Leibniz-Formel an.

Beispiel 1

Berechnen Sie das bestimmte Integral ∫ 1 3 x 2 d x mit der Newton-Leibniz-Formel.

Lösung

Bedenken Sie, dass der Integrand der Form y = x 2 vom Intervall [ 1 ; 3 ], dann ist es auf diesem Intervall integrierbar. Aus der Tabelle der unbestimmten Integrale sehen wir, dass die Funktion y = x 2 für alle viele Stammfunktionen hat echte Werte x, was x ∈ 1 bedeutet; 3 wird geschrieben als F (x) = ∫ x 2 d x = x 3 3 + C . Es ist notwendig, die Stammfunktion mit C = 0 zu nehmen, dann erhalten wir F (x) = x 3 3.

Wir verwenden die Newton-Leibniz-Formel und stellen fest, dass die Berechnung des bestimmten Integrals die Form ∫ 1 3 x 2 d x = x 3 3 1 3 = 3 3 3 - 1 3 3 = 26 3 annimmt.

Antwort:∫ 1 3 x 2 d x = 26 3

Beispiel 2

Berechnen Sie das bestimmte Integral ∫ - 1 2 x · e x 2 + 1 d x mit der Newton-Leibniz-Formel.

Lösung

Die gegebene Funktion ist stetig vom Segment [ - 1 ; 2 ], was bedeutet, dass es darauf integrierbar ist. Es ist notwendig, den Wert des unbestimmten Integrals ∫ x · e x 2 + 1 d x mithilfe der Methode der Subsumierung unter dem Differentialzeichen zu ermitteln. Dann erhalten wir ∫ x · e x 2 + 1 d x = 1 2 ∫ e x 2 + 1 d ( x 2 + 1) = 1 2 e x 2 + 1 + C .

Wir haben also eine Menge von Stammfunktionen der Funktion y = x · e x 2 + 1, die für alle x gelten, x ∈ - 1; 2.

Es ist notwendig, die Stammfunktion bei C = 0 zu nehmen und die Newton-Leibniz-Formel anzuwenden. Dann erhalten wir einen Ausdruck der Form

∫ - 1 2 x · e x 2 + 1 d x = 1 2 e x 2 + 1 - 1 2 = = 1 2 e 2 2 + 1 - 1 2 e (- 1) 2 + 1 = 1 2 e (- 1) 2 + 1 = 1 2 e 2 (e 3 - 1)

Antwort:∫ - 1 2 x e x 2 + 1 d x = 1 2 e 2 (e 3 - 1)

Beispiel 3

Berechnen Sie die Integrale ∫ - 4 - 1 2 4 x 3 + 2 x 2 d x und ∫ - 1 1 4 x 3 + 2 x 2 d x .

Lösung

Segment - 4; - 1 2 besagt, dass die Funktion unter dem Integralzeichen stetig, also integrierbar ist. Von hier aus finden wir die Menge der Stammfunktionen der Funktion y = 4 x 3 + 2 x 2. Wir verstehen das

∫ 4 x 3 + 2 x 2 d x = 4 ∫ x d x + 2 ∫ x - 2 d x = 2 x 2 - 2 x + C

Es ist notwendig, die Stammfunktion F (x) = 2 x 2 - 2 x zu nehmen, dann erhalten wir unter Anwendung der Newton-Leibniz-Formel das Integral, das wir berechnen:

∫ - 4 - 1 2 4 x 3 + 2 x 2 d x = 2 x 2 - 2 x - 4 - 1 2 = 2 - 1 2 2 - 2 - 1 2 - 2 - 4 2 - 2 - 4 = 1 2 + 4 - 32 - 1 2 = - 28

Wir fahren mit der Berechnung des zweiten Integrals fort.

Aus dem Segment [-1; 1 ] haben wir, dass die Integrandenfunktion als unbegrenzt gilt, weil lim x → 0 4 x 3 + 2 x 2 = + ∞ , dann folgt daraus eine notwendige Bedingung Integrierbarkeit aus einem Segment. Dann ist F (x) = 2 x 2 - 2 x keine Stammfunktion für y = 4 x 3 + 2 x 2 aus dem Intervall [ - 1 ; 1 ], da Punkt O zum Segment gehört, aber nicht im Definitionsbereich enthalten ist. Dies bedeutet, dass es ein bestimmtes Riemann- und Newton-Leibniz-Integral für die Funktion y = 4 x 3 + 2 x 2 aus dem Intervall [ - 1 ; 1 ] .

Antwort: ∫ - 4 - 1 2 4 x 3 + 2 x 2 d x = - 28 , es gibt ein bestimmtes Riemann- und Newton-Leibniz-Integral für die Funktion y = 4 x 3 + 2 x 2 aus dem Intervall [ - 1 ; 1 ] .

Bevor Sie die Newton-Leibniz-Formel verwenden, müssen Sie genau wissen, ob ein bestimmtes Integral existiert.

Ändern einer Variablen in einem bestimmten Integral

Wenn die Funktion y = f (x) definiert und stetig vom Intervall [ a ; b], dann ist die verfügbare Menge [a; b] gilt als der Wertebereich der Funktion x = g (z), definiert auf dem Segment α; β mit der vorhandenen stetigen Ableitung, wobei g (α) = a und g β = b, erhalten wir daraus ∫ a b f (x) d x = ∫ α β f (g (z)) g " (z) d z.

Diese Formel wird verwendet, wenn Sie das Integral ∫ a b f (x) d x berechnen müssen, wobei das unbestimmte Integral die Form ∫ f (x) d x hat. Wir berechnen es mit der Substitutionsmethode.

Beispiel 4

Berechnen Sie ein bestimmtes Integral der Form ∫ 9 18 1 x 2 x - 9 d x .

Lösung

Die Integrandenfunktion wird im Integrationsintervall als stetig betrachtet, was bedeutet, dass ein bestimmtes Integral existiert. Geben wir die Notation an, dass 2 x - 9 = z ⇒ x = g (z) = z 2 + 9 2. Der Wert x = 9 bedeutet, dass z = 2 9 - 9 = 9 = 3, und für x = 18 erhalten wir z = 2 18 - 9 = 27 = 3 3, dann g α = g (3) = 9, g β = g 3 3 = 18. Beim Einsetzen der erhaltenen Werte in die Formel ∫ a b f (x) d x = ∫ α β f (g (z)) g " (z) d z erhalten wir das

∫ 9 18 1 x 2 x - 9 d x = ∫ 3 3 3 1 z 2 + 9 2 · z · z 2 + 9 2 " d z = = ∫ 3 3 3 1 z 2 + 9 2 · z · z d z = ∫ 3 3 3 2 z 2 + 9 d z

Gemäß der Tabelle der unbestimmten Integrale haben wir, dass eine der Stammfunktionen der Funktion 2 z 2 + 9 den Wert 2 3 a r c t g z 3 annimmt. Wenn wir dann die Newton-Leibniz-Formel anwenden, erhalten wir das

∫ 3 3 3 2 z 2 + 9 d z = 2 3 a r c t g z 3 3 3 = 2 3 a r c t g 3 3 3 - 2 3 a r c t g 3 = 2 3 a r c t g 3 - a r c t g 1 = 2 3 π 3 - π 4 = π 18

Die Feststellung könnte ohne Verwendung der Formel ∫ a b f (x) d x = ∫ α β f (g (z)) · g " (z) d z erfolgen.

Wenn wir mit der Ersetzungsmethode ein Integral der Form ∫ 1 x 2 x - 9 d x verwenden, können wir zum Ergebnis ∫ 1 x 2 x - 9 d x = 2 3 a r c t g 2 x - 9 3 + C kommen.

Von hier aus führen wir Berechnungen mit der Newton-Leibniz-Formel durch und berechnen das bestimmte Integral. Wir verstehen das

∫ 9 18 2 z 2 + 9 d z = 2 3 a r c t g z 3 9 18 = = 2 3 a r c t g 2 18 - 9 3 - ar c t g 2 9 - 9 3 = = 2 3 a r c t g 3 - a r c t g 1 = 2 3 π 3 - π 4 = π 18

Die Ergebnisse waren die gleichen.

Antwort: ∫ 9 18 2 x 2 x - 9 d x = π 18

Teilweise Integration bei der Berechnung eines bestimmten Integrals

Wenn auf dem Segment [ a ; b ] sind die Funktionen u (x) und v (x) definiert und stetig, dann sind ihre Ableitungen erster Ordnung v " (x) · u (x) integrierbar, also aus diesem Segment für die integrierbare Funktion u " (x) · v ( x) die Gleichheit ∫ a b v " (x) · u (x) d x = (u (x) · v (x)) a b - ∫ a b u " (x) · v (x) d x ist wahr.

Die Formel kann dann verwendet werden, es ist notwendig, das Integral ∫ a b f (x) d x zu berechnen, und ∫ f (x) d x es war notwendig, es durch partielle Integration zu suchen.

Beispiel 5

Berechnen Sie das bestimmte Integral ∫ - π 2 3 π 2 x · sin x 3 + π 6 d x .

Lösung

Die Funktion x · sin x 3 + π 6 ist im Intervall - π 2 integrierbar; 3 π 2, was bedeutet, dass es stetig ist.

Sei u (x) = x, dann d (v (x)) = v " (x) d x = sin x 3 + π 6 d x, und d (u (x)) = u " (x) d x = d x, und v (x) = - 3 cos π 3 + π 6 . Aus der Formel ∫ a b v " (x) · u (x) d x = (u (x) · v (x)) a b - ∫ a b u " (x) · v (x) d x erhalten wir das

∫ - π 2 3 π 2 x · sin x 3 + π 6 d x = - 3 x · cos x 3 + π 6 - π 2 3 π 2 - ∫ - π 2 3 π 2 - 3 cos x 3 + π 6 d x = = - 3 · 3 π 2 · cos π 2 + π 6 - - 3 · - π 2 · cos - π 6 + π 6 + 9 sin x 3 + π 6 - π 2 3 π 2 = 9 π 4 - 3 π 2 + 9 sin π 2 + π 6 - sin - π 6 + π 6 = 9 π 4 - 3 π 2 + 9 3 2 = 3 π 4 + 9 3 2

Das Beispiel lässt sich auch anders lösen.

Finden Sie die Menge der Stammfunktionen der Funktion x · sin x 3 + π 6 durch partielle Integration mit der Newton-Leibniz-Formel:

∫ x · sin x x 3 + π 6 d x = u = x , d v = sin x 3 + π 6 d x ⇒ d u = d x , v = - 3 cos x 3 + π 6 = = - 3 cos x 3 + π 6 + 3 ∫ cos x 3 + π 6 d x = = - 3 x cos x 3 + π 6 + 9 sin x 3 + π 6 + C ⇒ ∫ - π 2 3 π 2 x sin x 3 + π 6 d x = - 3 cos x 3 + π 6 + 9 sincos x 3 + π 6 - - - 3 - π 2 cos - π 6 + π 6 + 9 sin - π 6 + π 6 = = 9 π 4 + 9 3 2 - 3 π 2 - 0 = 3 π 4 + 9 3 2

Antwort: ∫ x · sin x x 3 + π 6 d x = 3 π 4 + 9 3 2

Wenn Sie einen Fehler im Text bemerken, markieren Sie ihn bitte und drücken Sie Strg+Eingabetaste

Durch ein bestimmtes Integral aus kontinuierliche Funktion F(X) auf dem letzten Segment [ A, B] (wobei ) das Inkrement einiger seiner Stammfunktionen in diesem Segment ist. (Im Allgemeinen wird das Verständnis spürbar einfacher, wenn Sie das Thema des unbestimmten Integrals wiederholen.) In diesem Fall wird die Notation verwendet

Wie in den folgenden Diagrammen zu sehen ist (das Inkrement der Stammfunktion wird durch angezeigt), Das bestimmte Integral kann entweder positiv oder sein negative Zahl (Er wird als Differenz zwischen dem Wert der Stammfunktion in der Obergrenze und ihrem Wert in der Untergrenze berechnet, d. h. als F(B) - F(A)).

Zahlen A Und B werden als untere bzw. obere Integrationsgrenze bezeichnet, und das Segment [ A, B] – Segment der Integration.

Also, wenn F(X) – eine Stammfunktion für F(X), dann ist laut Definition

(38)

Gleichheit (38) heißt Newton-Leibniz-Formel . Unterschied F(B) – F(A) ist kurz wie folgt geschrieben:

Daher schreiben wir die Newton-Leibniz-Formel wie folgt:

(39)

Beweisen wir, dass das bestimmte Integral nicht davon abhängt, welche Stammfunktion des Integranden bei der Berechnung verwendet wird. Lassen F(X) und F( X) sind beliebige Stammfunktionen des Integranden. Da es sich um Stammfunktionen derselben Funktion handelt, unterscheiden sie sich durch einen konstanten Term: Ф( X) = F(X) + C. Deshalb

Dies stellt fest, dass auf dem Segment [ A, B] Inkremente aller Stammfunktionen der Funktion F(X) zusammenpassen.

Um ein bestimmtes Integral zu berechnen, ist es daher notwendig, eine beliebige Stammfunktion des Integranden zu finden, d.h. Zuerst muss man es finden unbestimmtes Integral. Konstante MIT von späteren Berechnungen ausgeschlossen. Dann wird die Newton-Leibniz-Formel angewendet: Der Wert der Obergrenze wird in die Stammfunktion eingesetzt B , weiter - der Wert der Untergrenze A und die Differenz wird berechnet F(b) - F(a) . Die resultierende Zahl ist ein bestimmtes Integral..

Bei A = B per Definition akzeptiert

Beispiel 1.

Lösung. Finden wir zunächst das unbestimmte Integral:

Anwendung der Newton-Leibniz-Formel auf die Stammfunktion

(bei MIT= 0), erhalten wir

Bei der Berechnung eines bestimmten Integrals ist es jedoch besser, die Stammfunktion nicht separat zu finden, sondern das Integral sofort in die Form (39) zu schreiben.

Beispiel 2. Bestimmtes Integral berechnen

Lösung. Formel verwenden

Eigenschaften des bestimmten Integrals

Satz 2.Der Wert des bestimmten Integrals hängt nicht von der Bezeichnung der Integrationsvariablen ab, d.h.

(40)

Lassen F(X) – Stammfunktion für F(X). Für F(T) Die Stammfunktion ist die gleiche Funktion F(T), bei dem die unabhängige Variable nur anders bezeichnet wird. Somit,

Basierend auf Formel (39) bedeutet die letzte Gleichheit die Gleichheit der Integrale

Satz 3.Der konstante Faktor kann aus dem Vorzeichen des bestimmten Integrals entnommen werden, d.h.

(41)

Satz 4.Bestimmtes Integral einer algebraischen Summe endliche Zahl Funktionen ist gleich algebraische Summe bestimmte Integrale dieser Funktionen, d.h.

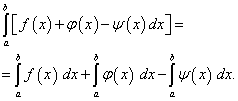(42)

Satz 5.Wenn ein Integrationssegment in Teile unterteilt wird, ist das bestimmte Integral über das gesamte Segment gleich der Summe der bestimmten Integrale über seine Teile, d.h. Wenn

(43)

Satz 6.Bei der Neuordnung der Grenzen der Integration Absolutwert Das bestimmte Integral ändert sich nicht, sondern nur sein Vorzeichen, d.h.

(44)

Satz 7(Mittelwertsatz). Bestimmtes Integral gleich dem Produkt Länge des Integrationssegments zum Wert des Integranden an einem Punkt darin, d.h.

(45)

Satz 8.Wenn die obere Integrationsgrenze größer als die untere ist und der Integrand nicht negativ (positiv) ist, dann ist auch das bestimmte Integral nicht negativ (positiv), d. h. Wenn

Satz 9.Wenn die obere Integrationsgrenze größer als die untere ist und die Funktionen stetig sind, dann liegt die Ungleichung vor

können Term für Term integriert werden, d.h.

(46)

Die Eigenschaften des bestimmten Integrals ermöglichen es, die direkte Berechnung von Integralen zu vereinfachen.

Beispiel 5. Bestimmtes Integral berechnen

Unter Verwendung der Sätze 4 und 3 und beim Finden von Stammfunktionen - Tabellenintegralen (7) und (6) erhalten wir

Bestimmtes Integral mit variabler Obergrenze

Lassen F(X) – kontinuierlich auf dem Segment [ A, B] Funktion und F(X) ist seine Stammfunktion. Betrachten Sie das bestimmte Integral

(47)

Und durch T Die Integrationsvariable ist so bezeichnet, dass sie nicht mit verwechselt wird Höchstgrenze. Wenn es sich ändert X auch das bestimmte Integral (47) ändert sich, d.h. es ist eine Funktion der oberen Integrationsgrenze X, was wir mit bezeichnen F(X), d.h.

(48)

Beweisen wir die Funktion F(X) ist eine Stammfunktion für F(X) = F(T). Tatsächlich differenzierend F(X), wir bekommen

als F(X) – Stammfunktion für F(X), A F(A) ist ein konstanter Wert.

Funktion F(X) - einer von Unendliche Nummer Stammfunktionen für F(X), nämlich diejenige, die X = A geht auf Null. Diese Aussage erhält man, wenn wir in Gleichung (48) setzen X = A und verwenden Sie Satz 1 des vorherigen Absatzes.

Berechnung bestimmter Integrale nach der Methode der partiellen Integration und der Methode der Variablenänderung

wo per Definition F(X) – Stammfunktion für F(X). Wenn wir die Variable im Integranden ändern

dann können wir gemäß Formel (16) schreiben

In diesem Ausdruck

Stammfunktion für

Tatsächlich ist seine Ableitung laut Differenzierungsregel komplexer Funktionen, ist gleich

Seien α und β die Werte der Variablen T, für die die Funktion

nimmt Werte entsprechend an A Und B, d.h.

Aber nach der Newton-Leibniz-Formel ist der Unterschied F(B) – F(A) Es gibt

Betrachten wir die Funktion. Diese Funktion heißt: Integral als Funktion der Obergrenze. Beachten wir einige Eigenschaften dieser Funktion.
Satz 2.1. Wenn f(x) eine integrierbare Funktion ist, dann ist Ф(x) stetig auf .
Nachweisen. Nach Eigenschaft 9 des bestimmten Integrals (Mittelwertsatz) gilt , von wo aus wir bei , das Erforderliche erhalten.
Satz 2.2. Wenn f(x) eine stetige Funktion auf ist, dann ist Ф’(x) = f(x) auf .
Nachweisen. Nach Eigenschaft 10 des bestimmten Integrals (zweiter Mittelwertsatz) gilt Wo Mit– Irgendwann im Segment. Aufgrund der Stetigkeit der Funktion f erhalten wir
Somit ist Ф(x) eine der Stammfunktionen der Funktion f(x), daher gilt Ф(x) = F(x) + C, wobei F(x) eine weitere Stammfunktion von f(x) ist. Da außerdem Ф(a) = 0 ist, gilt 0 = F(a) + C, also C = -F(a) und daher Ф(x) = F(x) – F(a). Unter der Annahme x=b erhalten wir die Newton-Leibniz-Formel

Beispiele
1.

Teilweise Integration in ein bestimmtes Integral

Das bestimmte Integral behält die Formel für die partielle Integration bei. In diesem Fall nimmt es die Form an

Beispiel.

Variablen in einem bestimmten Integral ändern

Eine der Ergebnisvarianten zur Änderung von Variablen in einem bestimmten Integral ist wie folgt.
Satz 2.3. Sei f(x) auf dem Segment stetig und erfülle die Bedingungen:
1) φ(α) = a
2) φ(β) = b
3) Die Ableitung φ’(t) ist überall im Intervall [α, β] definiert
4) für alle t aus [α, β]
Dann
Nachweisen. Wenn F(x) eine Stammfunktion für f(x)dx ist, dann ist F(φ(t)) eine Stammfunktion für Daher ist F(b) – F(a) = F(φ(β)) – F(φ(α)) . Der Satz ist bewiesen.
Kommentar. Wenn wir die Stetigkeit der Funktion f(x) unter den Bedingungen von Satz 2.3 ablehnen, müssen wir die Monotonie der Funktion φ(t) fordern.

Beispiel. Berechnen Sie das Integral. Setzen wir: Dann ist dx = 2tdt und daher